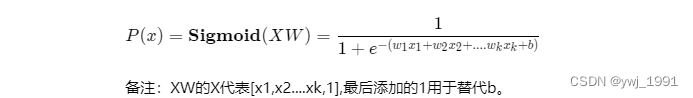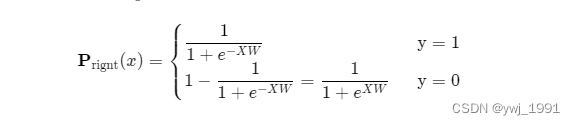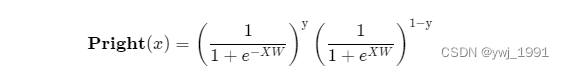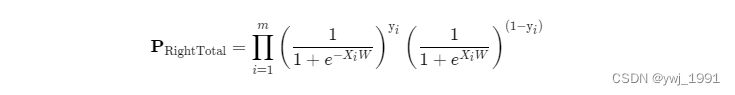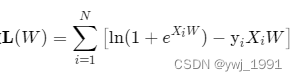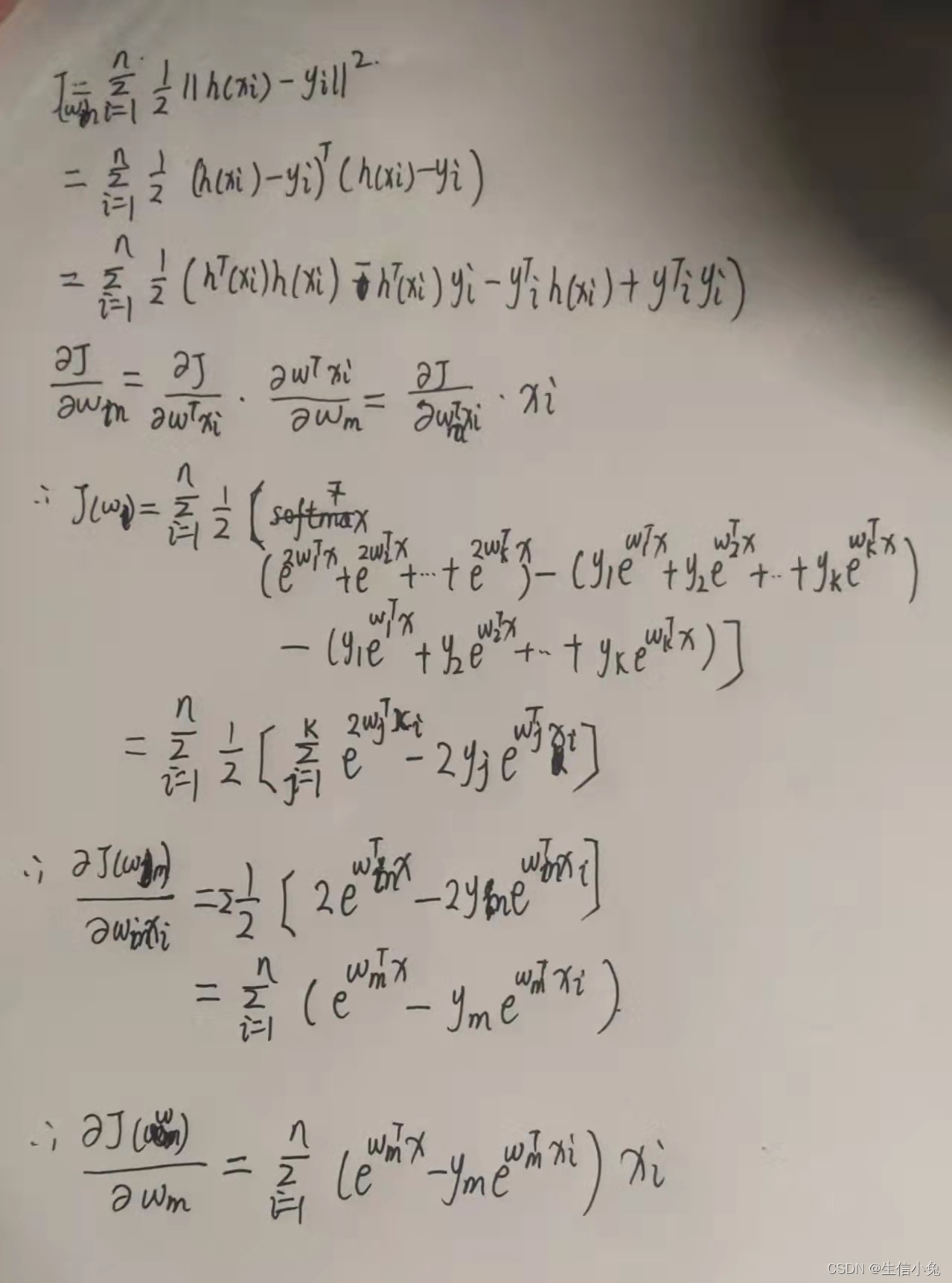入门篇(二)模型：逻辑回归(一步步从原理到实现)

《老饼讲解机器学习》专注于机器学习的学习网站http://ml.bbbdata.com/teach#187

一、问题

二、逻辑回归的思想

三、模型表达式

四、损失函数

(一) 单个样本评估正确的概率

(二) 所有样本评估正确的概率

(三) 损失函数

(四) 总结

五、模型求解

(一) 梯度下降算法

(二) 梯度公式

(三) 梯度下降算法应用于逻辑回归

六、实例解说

(一) 问题

(二) 建模思路

(三) 代码实现

(四) 模型结果

(五) 检验模型效果

七、本文总结

(一) 学习了逻辑回归模型原理

(二) 梯度下降法求解逻辑回归

八、附件

本文讲解机器学习入门第二个经典模型--逻辑回归！
好话不嫌多，机器学习的主要任务就是进行预测。

一、问题

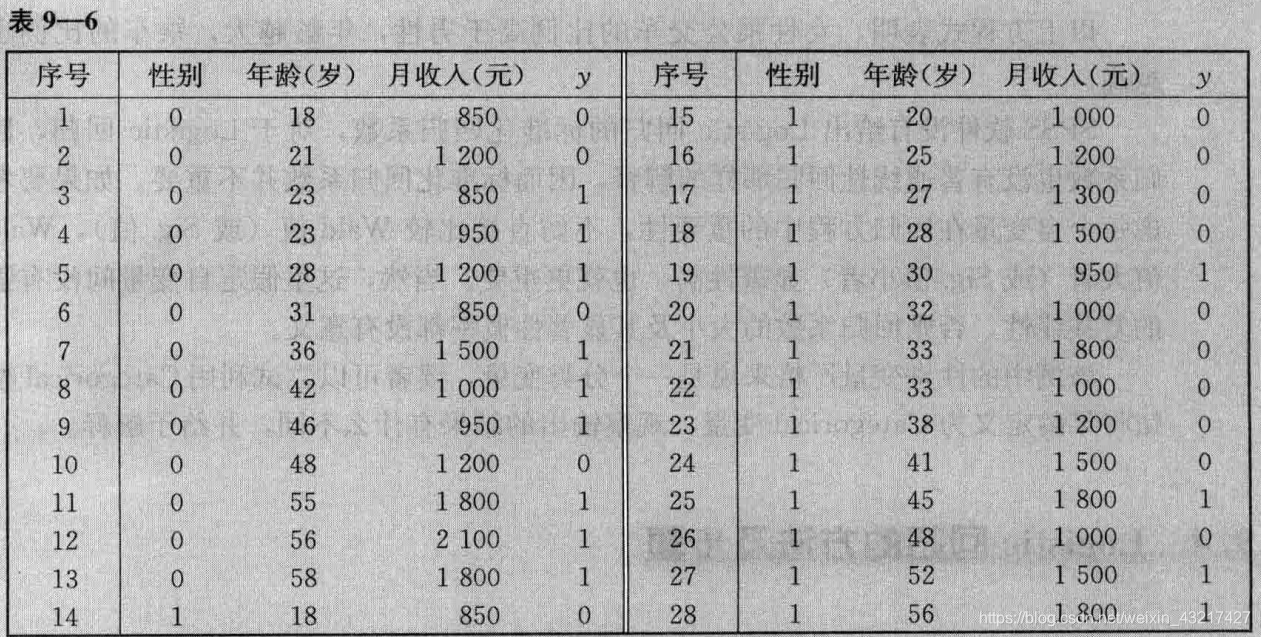
现在有一组数据，需要利用各个特征去预测目标的类别是1还是0：

mean smoothness	mean compactness	mean concavity	mean concave points	是否良性
0.1184	0.2776	0.3001	0.1471	0
0.08474	0.07864	0.0869	0.07017	0
...	...	...	...	...
0.08752	0.07698	0.04751	0.03384	1
0.08261	0.04751	0.01972	0.01349	1
...	...	...	...	...
0.09752	0.1141	0.09388	0.05839	0
...	...	...	...	...
0.08455	0.1023	0.09251	0.05302	0
0.1178	0.277	0.3514	0.152	0
0.05263	0.04362	0.0	0.0	1

二、逻辑回归的思想

我们知道，线性回归拟合的是数值，并不符合我们预测类别的需求。
但数值与类别也是有关联的。例如，天色越黑，下雨概率就越大。即值越大，属于某类别的概率也越大。值与概率之间可以互转。

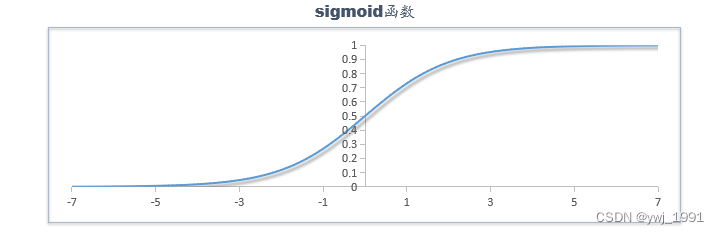
在数学里通常用 $\textbf{Sigmoid}(x) = \dfrac{1}{1+e^{-x}}$ 函数将数值转化为概率：

逻辑回归就是这样的原理，先用 wx+b 作为综合值的评估，再套用 sigmoid 函数将综合评估值转为概率。所以，逻辑回归本骨子里还是线性模型。

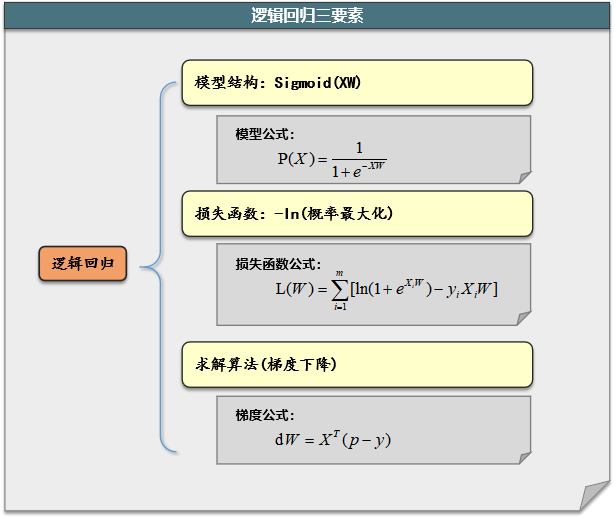
三、模型表达式

逻辑回归的模型表达式如下：

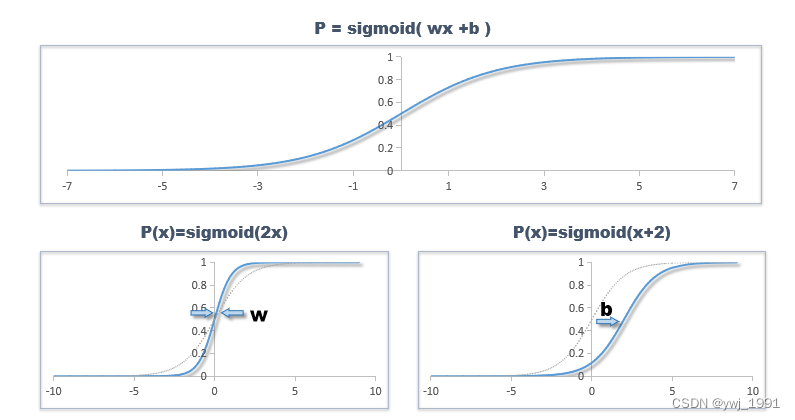
在单变量时，它就是一条S曲线，其中，w控制了它的拉伸，b则控制了它的平移位置：

类似地，在两个变量时，它就是一个S面，在更多变量时，则是一个超S面。

四、损失函数

我们知道，损失函数引导我们去求取模型里的参数w和b，也就是指明我们想要一个什么样的w,b。
在逻辑回归中，我们用误差就不适合了。逻辑回归模型采用的是，模型预测正确概率最大化~！

(一) 单个样本评估正确的概率

模型对单个样本评估正确的概率 $\textbf{P}_{\text{right}}(x)$ 为：

解析：逻辑回归的输出就是类别1的概率，真实值也为1 时, P就是评估正确的概率 ; y= 0时,P是错误的概率，1-P 就是模型正确的概率。

巧妙的操作是，可以用一条式子把上述二式合并如下:

解析：当y=1时，第二个括号等于1，当y=0时，第一个括号为0.与上述二式一致。

(二) 所有样本评估正确的概率

假设每个样本是独立事件，则总评估正确的概率为所有样本评估正确的积：

(三) 损失函数

我们期待 $\textbf{P}_{\text{RightTotal}}$ 最大化，只要将损失函数设计成 $-\textbf{P}_{\text{RightTotal}}$ 即可。又由于 $\textbf{P}_{\text{RightTotal}}$ 中含有大量的乘号，为计算方便，我们外套一个对数。

最后，损失函数设计如下：

说明：
在连乘的情况下，使用对数使其转为加号是常用的操作。因为对数是单调函数，能让P最大化的W，同样会是令lnP最大化的W。

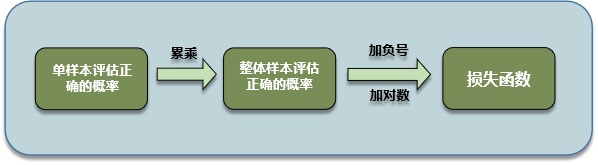
(四) 总结

逻辑回归损失函数设计的整体思路为：

这种思路设计的损失函数也叫最大似然损失函数。

五、模型求解

模型求解的技术背景

现在我们需要求解最佳的W，使损失函数

最小。也即令预测概率准确性最大化。

理论上，我们可以求损失函数的偏导，k+1个参数的偏导共k+1个方程，再联立求解即可。但遗憾的是，它的偏导数是非线性方程，我们没有能力去求解k+1个非线性方程的解。

因此，我们退而求其次，使用算法去寻找一个优秀解。其中，梯度下降法就是一个经典的数值求解算法。

(一) 梯度下降算法

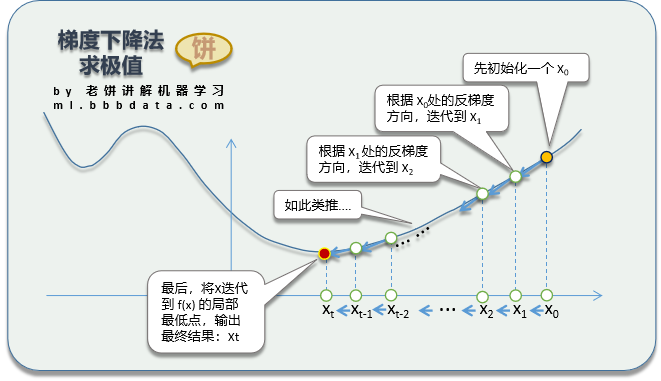
其原理如下：

即先初始化一个初始解，然后不断地根据目标函数的梯度下降方向，调整x,最后达到局部最优值。具体理论请看《入门篇-求解算法：梯度下降》。

(二) 梯度公式

梯度下降法在迭代过程使用到了L(W)的梯度，我们需要求出L(W)的梯度公式（公式详细推导在文未给出）：

$\displaystyle \dfrac{\partial L(W)}{\partial W}= X^T(p-\text{y})$

其中
(1) X 为m*n矩阵, m样本数, n为特征个数,即一行为一个样本,一列为一特征.
(2) y,p 为列向量, $p = \dfrac{1}{1+e^{-XW}}$
(3) W为列向量n*1的列向量

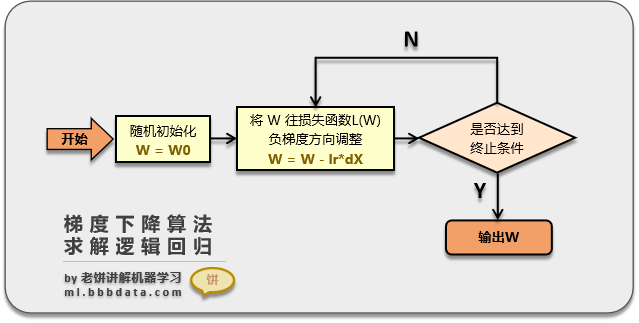
(三) 梯度下降算法应用于逻辑回归

先初始化W，然后
(1) 按照梯度公式算出梯度，
(2) 将W往负梯度方向调整
不断循环(1)和(2)，直到达到终止条件(例如达到最大迭代次数)

Pass: 工具包里通常不使用梯度下降算法，对于逻辑回归，会有更巧妙的求解算法，例如matlab工具箱里使用的就是牛顿法，它与梯度下降法思想类似。
在这里我们先学习梯度下降法求解，它是最经典必学的求解算法，没有之一。它简单，普适性广，通用。至于工具箱中使用的算法，在进阶篇我们再进行讲解。

六、实例解说

(一) 问题

以sk-learn中的breast_cancer的部分数据为例 ，
已采集150组乳腺癌数据：包含四个特征和乳腺癌类别（特征：平均平滑度、平均紧凑度、平均凹面、平均凹点，类别：恶性、良性）。
具体数据如下：

mean smoothness mean compactness mean concavity mean concave points 是否良性
0.1184 0.2776 0.3001 0.1471 0
0.08474 0.07864 0.0869 0.07017 0
0.1096 0.1599 0.1974 0.1279 0
... ... ... ... ...
0.08752 0.07698 0.04751 0.03384 1
0.08637 0.04966 0.01657 0.01115 1
0.07685 0.06059 0.01857 0.01723 1
0.08261 0.04751 0.01972 0.01349 1
... ... ... ... ...
0.09752 0.1141 0.09388 0.05839 0
0.09488 0.08511 0.08625 0.04489 0
... ... ... ... ...
0.1178 0.277 0.3514 0.152 0
0.05263 0.04362 0.0 0.0 1

现在需要我们可以通过数据，训练一个决策模型，用于预测乳腺癌是良性还是恶性。

(二) 建模思路

1、假设X和Y符合逻辑回归模型，则有 $\textbf{y} = \textbf{sigmoid}(XW)$
2、用梯度下降法求解W：
用梯度下降法求解损失函数中的W：先初始化一个w,然后不断按负梯度方向 $\displaystyle \dfrac{\partial L(W)}{\partial W}= X^T(p-\text{y})$ 调整。
（最好能将数据归一化，这里为简化，我们不作归一化）
3、将W回代模型

(三) 代码实现

python代码如下:

# -*- coding: utf-8 -*-
"""
梯度下降求解逻辑回归
"""
from sklearn.datasets import load_breast_cancer
import numpy as np
#----数据加载------
data = load_breast_cancer()
X    = data.data[:,4:8]
y    = data.target#-----给x增加一列1---------
xt = np.insert(X, X.shape[1], 1, axis=1)#-----梯度下降求解w---------------
np.random.seed(888)             # 设定随机种子，以确保每次程序结果一次
w = np.random.rand(xt.shape[1]) # 初始化
for i in range(10000):p = 1/(1+np.exp(-xt@w)) #计算pw = w - 0.01*(xt.T@(p-y)) # 往负梯度方向更新w
p = 1/(1+np.exp(-xt@w))  # 最终的预测结果
print("参数w："+str(w))

运行后输出：

参数w：[  7.16215375  14.98708501 -16.84689114 -73.92486786   3.38331608]

(四) 模型结果

将w回代模型，我们可以得到模型：

$\textbf{p} = \dfrac{1}{1+ e^{-(7.16*x_1+ 14.98*x_2 -16.84x*_3 -73.92*x_4 +3.38)}}$

(五) 检验模型效果

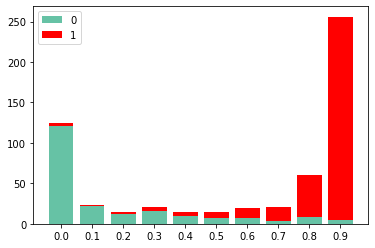
我们画出训练样本中，各个p值段的0，1标签分布：

可以看到，p值越高，属于1类别的就越多，模型对样本已有较好的区分度。

附：使用sklearn包求解逻辑回归

实际中我们一般都会直接调包求解，这里给出调用 sklearn包的方法
代码如下：

from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
import numpy as np
#----数据加载------
data = load_breast_cancer()
X    = data.data[:,4:8]
y    = data.targetnp.random.seed(888)
#-----训练模型--------------------
clf = LogisticRegression(random_state=0)            
clf.fit(X,y) 
#------打印结果------------------------
print("模型参数："+str(clf.coef_))
print("模型阈值："+str(clf.intercept_))

运行结果：

模型参数：[[-0.53024026 -3.48636783 -6.89132654 -4.37965412]]
模型阈值：[1.80112869]

七、本文总结

(一) 学习了逻辑回归模型原理

逻辑回归模型是用于做二分类。输出属于分类1的概率。
(1) 模型函数：相当于用线性函数综合所有变量，再用sigmoid函数将综合值转为概率值。
$P(x) = \textbf{Sigmoid}(XW) = \dfrac{1}{1+e^{-(w_1x_1+w_2x_2+....w_kx_k+b)}}$
(2) 模型的损失函数
用概率最大化作为损失函数，即取何值时，模型预测正确的概率最大。
(3) 模型求解
模型无法求得精确解，使用梯度下降等算法进行数值求解(matlab的逻辑回归包里用的是牛顿法，与梯度下降法思想类似)。