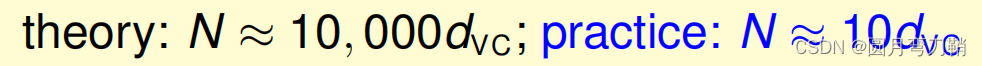机器学习基石——作业2解答

这里的$μ$指的是某个$h(x)≈f(x)$，对应的$E_{out}(h)$。其中目标函数$f(x)$是确定性的，没有噪声干扰。如果加上噪声，目标函数变为课中讲的概率分布$P(y│x)$，表示为

$$\begin{equation} P(y│x) = \left\{\begin{array}{lcl}{\lambda} &y=f(x) \\{1-\lambda} &{otherwize} \end{array} \right. \end {equation}$$
此时的 $f(x)$为ideal mini-target function，错误的概率为 $1-λ$。求此时的错误率。两部分：
①无噪声干扰的 $y$乘以对应的错误率；②在正确分类$y$的部分中，包含的由于噪声被flipped的 $y$。
$$P[y=f(x)]\bullet E_{out} (h)+P[y≠f(x)]\bullet(1-E_{out} (h))$$

求解: $μλ+(1-λ)(1-μ)=1+μ(2λ-1)-λ$，要消除$μ，λ=0.5$

MATLAB作图求解。错误率0.05时, $N$=453000, 最接近的是460000。

d=10,delta=0.05;
x=linspace(0,1000000,100000);
y=4*(2*x).^d.*exp(-0.125*x*delta^2);
loglog(x,y)

MATLAB求解。x3、x4用solve函数求解非线性方程。最小的是x4, Devroye。

N=10000;delta=0.05;d=50;
x1=sqrt(8/N*log(4*(2*N)^d/delta))
x2=sqrt(2*log(2*N*(N)^d)/N)+sqrt(2/N*log(1/delta))+1/N
x3=solve('sqrt(1/10000*(2*x3+log(6*(2*10000)^50/0.05)))=x3','x3')
x4=solve('x4=sqrt(1/20000*(4*x4*(1+x4)+log(4*(10000^2)^50/0.05)))','x4')
x5=sqrt(16/N*log(2*(N)^d/sqrt(delta))) 
%N=10000: x1=0.6322, x2=0.3313, x3=0.2237, x4=0.2152, x5=0.8604

上一问中令$N$=5。最小的是x3，Parondo and Van den Broek。

%N=5: x1=13.8282, x2=7.0488, x3=5.1014, x4=15.0125, x5=16.2641

题目十分类似高中排列组合中的“捆绑问题”。

假设$N=4$, 有$5$个间隔。首先考虑捆绑在一起的为正，其余的为负，则有$C_{4+1}^2$ 种。再反过来，将捆绑在一起的为负，其余的为正，又有$C_{4+1}^2$ 种。但是有重复情况：
正$(1,2),(1,3),(1,4), (5,4),(5,3),(5,2)$由于有边界位置“1”“5”，每种情况中未捆绑的剩余部分都是连续的，在负的情形中会重复计数。共有2×(4-1)种。
总结：$2C_{N+1}^2-2{N-1}=N^2-N+2$

	N=1	N=2	N=3	N=4
$m_{\mathcal{H}}(N)=N^2-N+2$	2	4	8	14
$2^N$	2	4	8	16

所以$d_{vc}=3$

环内的是正，环外的是负。不难观察，这是一个positive interval的问题，$m_{\mathcal{H}} (N)=C_{N+1}^2+1$

可以从多项式的根的个数的角度考虑。实轴上有$N$个点，要用多项式曲线将他们“打散”，多项式要有$N+1$个根，即$N+1$次多项式（代数基本定理）。可以考虑三次多项式曲线“打散”实轴上2个点的情况。

题目的公式不大懂，可参考http://beader.me/2014/02/22/vc-dimension-three/ 考虑了一个简化的决策树模型。按照描述，二维空间内，2个互相垂直且不相关的直线可以打散$2^2$个点，3维空间中3个互相垂直且不相关的平面可以打散$2^3$个点。

三角波，参数控制的是波的周期，因此显然是所有$N$都能打散。

答案选3.
选项1：括号内的不会比$N$大，因此不可能是$m_{\mathcal{H}}(N)$的上界；
选项2：这是个常数，不可能是上界；
选项3：$m_{\mathcal{H}}(N)$的一个上界是$2^N$，$2^{i}m_{\mathcal{H}}(N-i)$对应过去的上界就是$2^i·2^(N-i)=2^N$
选项4：$N^{d_{vc} }$是$m_{\mathcal{H}}(N)$的上界，但是开平方就不一定了。考虑课上讲的2D 感知机模型$N=4$时，$m_{\mathcal{H}}(4)=14，\sqrt{4^3 }=8<14$

答案选2。此题不是很懂第二个选项。当$d_{vc}=∞$时，$m_{\mathcal{H}}(N)=2^N$；当假设空间没有自由度时，可能只有1种$h$；第6题的答案就是$N^2-N+2$.
第二个选项随着$N$从1增大，依次是$1，1，1，2，2，…$,可能因为随着$N$增大，存在不增长和突然增长的情况。

求假设空间的交集的VC维。最小为0（没有交集），最大是假设空间中$d_{vc}$最大的那个（其他所有假设空间都被其包含）。所以选3。

求假设空间的并集的VC维。最小的情形下，也是假设空间中$d_{vc}$最大的那个。参考了Mac Jiang的博客http://blog.csdn.net/a1015553840/article/details/51043019的解释：
试想，有一个$h_1$，把平面所有点分为$+1$，$h_2$把平面所有点分为$-1$。$h_1∪h_2$的话，VC dimension为1，而各自$d_{vc}$加起来为0。所以选4.
详细的解释还可以参考http://beader.me/2014/02/22/vc-dimension-three/

16-20题考虑了一个一维决策树（即课上练习题讲的positive and negative rays模型），一共有$2N$种可能的$h$，由参数$s$（取$+1$和$-1$，表示取positive ray还是negative ray）和$θ$（对应阈值）决定。
如果训练集中有$N$个点（在实轴上），则$θ$最多有$N+1$种选择(不管$s$参数导致的重复)，可以设为$N$个点，每相邻两点的中间位置即均值（或在之间任意取值）。由于数目较少，可以穷举。
16题问的是$E_{out}$,可以和第1题联系起来，$E_{out}=μλ+(1-λ)(1-μ)=0.6μ+0.2$。错误率$20%$，即$λ=0.8$；由于区间在$[-1,1]$，区间长度为2，理想的$θ=0，s=+1$，$μ$的计算与$s$的符号有关：

$s=+1:$　　　　　　　　　　　　　　　　　　　$s=-1:$

$μ=|θ|/2$ 　　　　　　　　　　　　　　　　　　$μ=1-|θ|/2$
$E_{out1}=0.6μ+0.2=0.3|θ|+0.2$　　　　　　$E_{out2}=0.6μ+0.2=-0.3|θ|+0.8$

合并起来写:$E_{out}=(s+1)/2$
$E_{out1}+(1-s)/2 E_{out2}=0.5+0.3s(|θ|-1)$

此题统计$E_{in}$，算出0.15左右。
Python代码见http://blog.csdn.net/zyghs/article/details/78755242

此题统计$E_{out}$，算出0.25左右。
Python代码见http://blog.csdn.net/zyghs/article/details/78755242

19-20题用多维训练集，但是在每一维上用上一题的方法，找到维度i的最小$E_{in}$对应的$s_i$ 和$θ_i$，再从这些维度中找到最有区分度（$E_{in}$ 最小）的维度对应的$s_i$ 和$θ_i$。此题计算最小的$E_{in}$ 。算出0.25左右，Python代码见http://blog.csdn.net/zyghs/article/details/78755242

此题在测试集上计算最小的$E_{out}$，而不再用公式。算出0.35左右，
Python代码见http://blog.csdn.net/zyghs/article/details/78755242