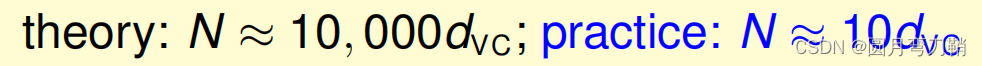机器学习基石 作业二
1 计算一下本来预测对与预测错时加上噪音导致的错误率然后相加即可。

2 选择一个 λ \lambda λ的值让 μ \mu μ的系数为0。

3 根据VC bound 公式带入计算即可,N=46000的时候error最接近0.05。下面的代码可以计算不同的N与目标error之间的差距。
def compute(N,err):delta = 0.05dvc = 10res = np.sqrt(8/N*np.log(4*pow(2*N,dvc)/delta))return res-err

4 编程计算这几个不等式的上限。感觉不是很有意思。将N=10000和N=5的时候分别带入看哪个最小即可。有两个隐函数需要使用sympy.solve来当做等式解方程。代码如下:
dvc = 50
delta = 0.05
N = 5def origiVC():return np.sqrt(8/N*np.log(4*pow(2*N,dvc)/delta))def rpVC():r1 = np.sqrt(2*np.log(2.0*N*pow(N,dvc))/N)r2 = np.sqrt(2/N*np.log(1/delta))return r1+r2+1/Ndef pvVC():epsilon = sympy.symbols('epsilon')r1 = sympy.solve(epsilon-sympy.sqrt(1/N*sympy.log(6*((2*N)**dvc)/delta)),epsilon)return r1def dVC():epsilon = sympy.symbols('epsilon')r1 = sympy.solve(epsilon-sympy.sqrt(0.5/N*(4*epsilon*(1+epsilon) + np.log(4)+dvc*sympy.log(N**2.0)-np.log(delta))),epsilon)return r1def vVC():return np.sqrt(16/N*(np.log(2)+dvc*np.log(N*1.0)-np.log(np.sqrt(delta))))if __name__ == '__main__':print(origiVC())print(rpVC())print(pvVC())print(dVC())print(vVC())
5.
6 做错了。看到个别人的一个解释。
https://blog.csdn.net/zyghs/article/details/78762070 这个老哥的博客里有这题稍微详细的解释。还是找规律写出通式,高中数学真重要.jpg

- 根据公式,VC维是3
8 还是将N=1开始慢慢找,发现N=3时能shatter的也是7种。因此得到答案。这相当于是一个二维的positive interval的题目。可以看ppt上关于Positive interval的假设,N个点,可以选择N+1个位置作为interval的起点或终点。每次的interval需要一个终点一个起点,也就是 C N + 1