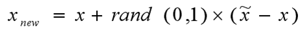SMOTE算法原理及Python代码实现

预备知识

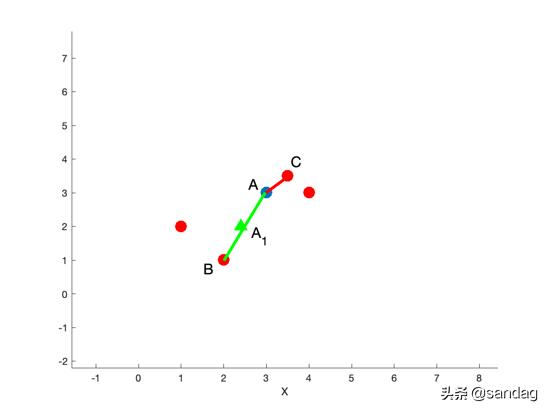
1. 向量代数的知识：对于点${\mathbf{x}}_1$和${\mathbf{x}}_2$，如果$\lambda \in [0,1]$，$\lambda {\mathbf{x}}_1+(1-\lambda ){\mathbf{x}}_2$肯定在点${\mathbf{x}}_1$和${\mathbf{x}}_2$的连线上。

2. 面向对象的设计思想就是抽象出一个类（Class），用的时候对类具体化成实例（Instance）。

• 类和实例

  首先，尝试创建一个Student类，代码如下：

  class Student(object):def __init__(self, name, score):self.name = nameself.score = score
  

  说明：

  class：定义类的关键字，创建类必须先写上；

  Student：类名，根据需要填写，类名首字母通常大写；

  (object)：表示该类是从哪个类继承来的，如果没有合适的继承类，就使用object类，这是所有类最终都会继承的类。

  __init__：类的一个特殊方法，创建实例时，会强制填写我们定义的属性，这里定义的属性是name和score。

  注意__init__前后分别有两个下划线。

  另外，__init__的第一个参数永远是self，表示创建的实例本身。因此，在__init__方法内部，就可以把各种属性绑定到self，因为self就指向创建的实例本身。

  定义好了Student类，就可以根据Student类创建出Student的实例，创建实例通过类名+()实现：

  bart = Student('Bart Simpson', 59)
  print(bart.name)
  print(bart.score)
  

  结果如下：

  Bart Simpson
  59
  

• 访问限制

  Class内部有属性（数据）和方法（函数），外部代码可以直接调用实例变量的方法来操作数据，这样就隐藏了内部的复杂逻辑。

  class Student(object):def __init__(self, name, score):self.name = nameself.score = scoredef lost_points(self):return 100 - self.scoredef print_score(self):print(' name : %s \n score : %s \n lost points : %s ' % (self.name, self.score, self.lost_points()))
  

  上面的代码创建了lost_points方法用于计算失分、print_score方法来输出结果，用以下代码测试效果：

  bart = Student('Bart Simpson', 59)
  bart.score = 99
  print(bart.lost_points())
  bart.print_score()
  

  结果如下：

  1name : Bart Simpson score : 99 lost points : 1 
  

  但是，外部代码可以自由地修改实例的属性name和score，为了不让外部访问内部属性，可以在属性名称前加上两个下划线__，使其变成私有变量（private），只有内部可以访问，外部无法访问。

  class Student(object):def __init__(self, name, score):self.__name = nameself.__score = scoredef lost_points(self):return 100 - self.__scoredef print_score(self):print('name : %s \nscore : %s \nlost points : %s ' % (self.__name, self.__score, self.lost_points()))
  

  bart = Student('Bart Simpson', 59)
  print(bart.__score)
  

  结果报错：

  AttributeError: 'Student' object has no attribute '__score'
  

  两个下划线__设置私有对方法（函数）同样有效，将lost_points设置为私有：

  class Student(object):def __init__(self, name, score):self.__name = nameself.__score = scoredef __lost_points(self):return 100 - self.__scoredef print_score(self):print('name : %s \nscore : %s \nlost points : %s ' % (self.__name, self.__score, self.__lost_points()))
  

  测试代码：

  bart = Student('Bart Simpson', 59)
  print(bart.__lost_points())
  

  结果同样报错：

  AttributeError: 'Student' object has no attribute '__lost_points'
  

以上的python面向对象编程的知识只限于后续内容理解所需，系统的教程请查看以下链接：

https://www.liaoxuefeng.com/wiki/1016959663602400/1017495723838528。

SMOTE算法内容的简单复习

先复习一下SMOTE算法都干了什么？

1. 对于少数类中每一个样本$x$，找到它在少数类中的k个近邻，k需要自己设定，一般为5。

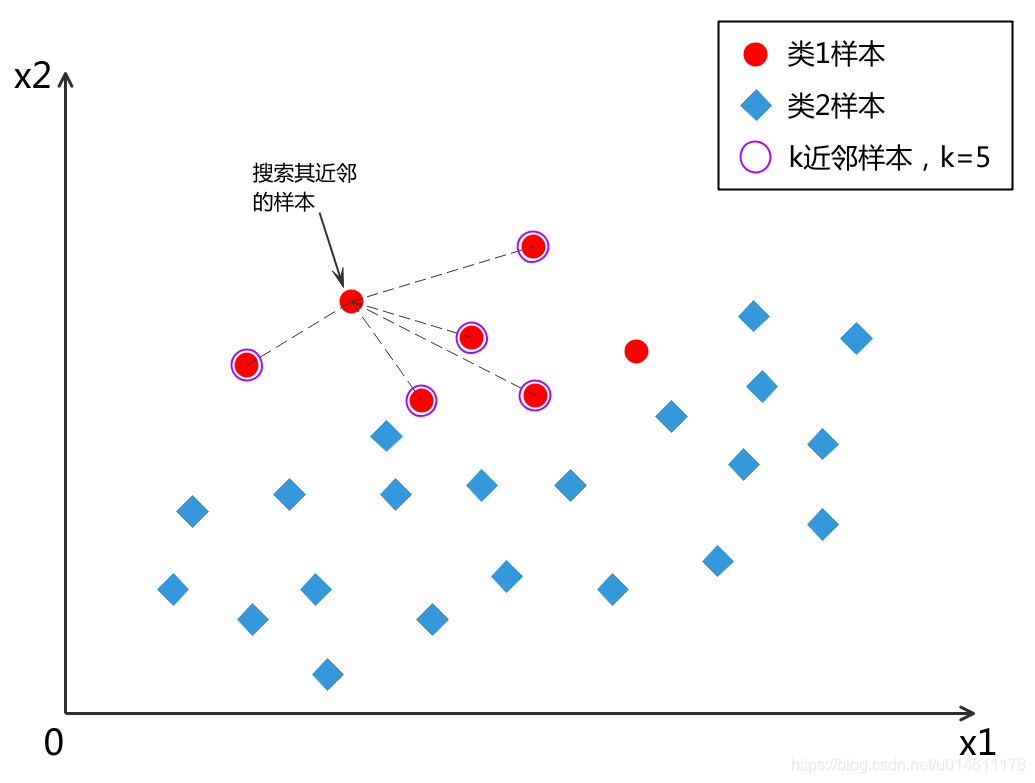
2. k个近邻中随机选一个样本$x_{近邻}$。

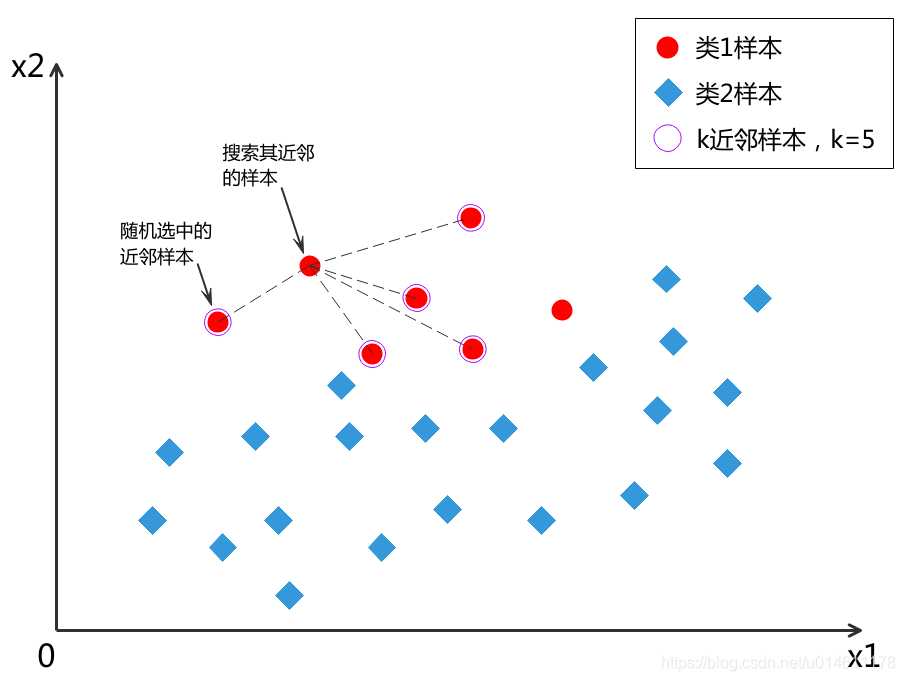
3. 生成一个0~1之间的随机数rand(0,1) ，用下式合成一个新样本：
$${\mathbf{x}}_{合成}=\mathbf{x}+rand(0,1)\ast ({\mathbf{x}}_{近邻}-\mathbf{x})$$
其中，${\mathbf{x}}_{合成}$表示最终合成的一个样本，

​ $\mathbf{x}$表示输入的一个少数类样本，

​ ${\mathbf{x}}_{近邻}$表示被选中的$x$的一个近邻样本，

​ $rand(0,1)$是0~1之间的一个随机数。

由于
$$\begin{array}{rl}{\mathbf{x}}_{合成}& =\mathbf{x}+rand(0,1)\ast ({\mathbf{x}}_{近邻}-\mathbf{x})\\ & =[1-rand(0,1)]\ast \mathbf{x}+rand(0,1)\ast {\mathbf{x}}_{近邻}\end{array}$$
根据预备知识中讲的向量代数内容，合成的样本是在$\mathbf{x}$和${\mathbf{x}}_{近邻}$连线上随机出现的一个点。

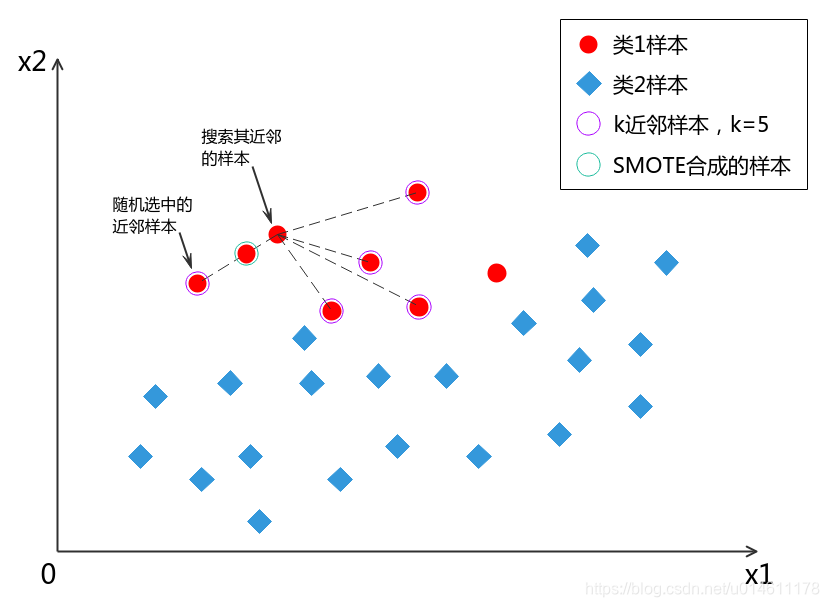
SMOTE算法的详细分析

有了以上对SMOTE算法的认识，下面根据原论文SMOTE: Synthetic Minority Over-sampling Technique的伪代码，给出算法的代码实现：

SMOTE算法论文链接：https://arxiv.org/pdf/1106.1813.pdf

代码实现会与原论文的伪代码在一些细节上有所不同，但大体思想是一样的。

先导入用到的工具包：

import random
from sklearn.neighbors import NearestNeighbors
import numpy as np

创建类对象和初始化

代码如下：

class Smote(object):def __init__(self, N=50, k=5, r=2):# 初始化self.N, self.k, self.r, self.newindexself.N = Nself.k = k# self.r是距离决定因子self.r = r# self.newindex用于记录SMOTE算法已合成的样本个数self.newindex = 0

依据python面向对象编程，首先建立一个名为Smote的类对象，括号()里面的object表示Smote继承自object（python最原始的对象就是object）。

接着，根据输入变量初始化Smote对象的变量，需要输入的变量包括：少数类样本samples，SMOTE算法合成的样本数量占原少数类样本的百分比N%，最近邻的个数k，近邻算法的距离决定因子r。

少数类样本samples放到后面的训练函数fit再输入初始化，那么需要初始化的是self.N，self.k，self.r，self.newindex。

self.r是距离决定因子，用于sklearn的k近邻算法NearestNeighbors的输入。

• self.r=2，最近邻算法采用欧式距离
• self.r=1，则是曼哈顿距离
• self.r取其他值，则采用明斯基距离

self.newindex用于记录SMOTE算法已合成的样本个数。

构建训练函数

代码如下：

def fit(self, samples):# 初始化self.samples, self.T, self.numattrsself.samples = samples# self.T是少数类样本个数，self.numattrs是少数类样本的特征个数self.T, self.numattrs = self.samples.shape# 查看N%是否小于100%if(self.N < 100):# 如果是，随机抽取N*T/100个样本，作为新的少数类样本np.random.shuffle(self.samples)self.T = int(self.N*self.T/100)self.samples = self.samples[0:self.T,:]# N%变成100%self.N = 100# 查看从T是否不大于近邻数kif(self.T <= self.k):# 若是，k更新为T-1self.k = self.T - 1# 令N是100的倍数N = int(self.N/100)# 创建保存合成样本的数组self.synthetic = np.zeros((self.T * N, self.numattrs))# 调用并设置k近邻函数neighbors = NearestNeighbors(n_neighbors=self.k+1, algorithm='ball_tree', p=self.r).fit(self.samples)# 对所有输入样本做循环for i in range(len(self.samples)):# 调用kneighbors方法搜索k近邻nnarray = neighbors.kneighbors(self.samples[i].reshape((1,-1)),return_distance=False)[0][1:]# 把N,i,nnarray输入样本合成函数self.__populateself.__populate(N, i, nnarray)# 最后返回合成样本self.syntheticreturn self.synthetic

为了和sklearn的用法保持一致，所以训练样本的函数用fit这个名字 。

下面是对代码的详细说明：

• 初始化

  # 初始化self.samples, self.T, self.numattrs
  self.samples = samples
  # self.T是少数类样本个数，self.numattrs是少数类样本的特征个数
  self.T, self.numattrs = self.samples.shape
  

  根据输入样本呢samples初始化self.samples, self.T, self.numattrs，T是少数类样本个数，numattrs是少数类样本的特征个数。

• 查看N%是否小于100%

  # 查看N%是否小于100%
  if(self.N < 100):# 如果是，随机抽取N*T/100个样本，作为新的少数类样本np.random.shuffle(self.samples)self.T = int(self.N*self.T/100)self.samples = self.samples[0:self.T,:]# N%变成100%self.N = 100
  

  若是，说明想要合成的样本要比原少数类样本少，那么，可以从原少数类样本中随机抽取N*T/100个样本，作为新的少数类样本，用于后续合成样本，另外要记得更新样本量T为N*T/100，N为100（更新N%为100%的意思是，合成样本量是新少数类样本量的100%）。

• 查看样本量T是否不大于近邻数k

  # 查看从T是否不大于近邻数k
  if(self.T <= self.k):# 若是，k更新为T-1self.k = self.T - 1
  

  若是，说明没有那么多样本用于搜索k近邻，干脆把k值减小，除去寻找近邻的样本本身，那就只剩k-1个。

• 创建保存合成样本的数组

  # 令N是100的倍数
  N = int(self.N/100)
  # 创建保存合成样本的数组
  self.synthetic = np.zeros((self.T * N, self.numattrs))
  

  令N = floor(N/100)，这么做的原因是想令从的数量是输入少数类样本数量的倍数。

  如一开始N% = 275%，经过上面运算，N% = 200%，也就是合成样本是输入少数类样本的2倍。

  floor是向下取整函数，python中int有相同的作用。

  确定倍数N就能创建保存合成样本的数组synthetic，行数为T*N，列数为特征数numattrs。

• 调用并设置k近邻函数

  # 调用并设置k近邻函数
  neighbors = NearestNeighbors(n_neighbors=self.k+1, algorithm='ball_tree', p=self.r).fit(self.samples)
  

  k近邻函数调用的是sklearn的NearestNeighbors。

  参数设置：

  • n_neighbors=self.k+1，这样设置的原因是NearestNeighbors会把原样本自己也算进近邻。
  • algorithm=‘ball_tree’，ball_tree是一种树搜索算法，这不是这里的重点，不用太关注。
  • p=self.r，就是输入距离决定因子，在创建类对象和初始化处已经详细介绍过，忘了的可以回头再看看。

  fit(self.samples)是因为需要输入样本来构建算法的树结构，方便后续快速搜索近邻。

• 搜索k近邻并调用合成样本函数

  # 对所有输入样本做循环
  for i in range(len(self.samples)):# 调用kneighbors方法搜索k近邻nnarray = neighbors.kneighbors(self.samples[i].reshape((1,-1)),return_distance=False)[0][1:]# 下面把N,i,nnarray输入样本合成函数self.__populateself.__populate(N, i, nnarray)# 最后返回合成样本self.syntheticreturn self.synthetic
  

  neighbors是之前设置好的NearestNeighbors对象，调用kneighbors方法就会返回两个数据：dist（到k个近邻的距离）和ind（k个近邻的索引）。

  参数设置：

  • return_distance设置为False，是为了不返回dist，因为我们只需要k个近邻的索引即可。
  • self.samples[i]要做reshape((1,-1))的原因是，self.samples是个二维数组array([[],[],…,[]])，self.samples[i]相当于取第i个一维列表[]，但是kneighbors要求输入样本必须是二维的，所以通过reshape((1,-1))将一维列表变成1行x列的二维数组，x表示任意数（reshape设置为-1表示依据输入决定当前维度大小），依具体的输入而定。

  kneighbors的输出ind取[0][1:]的原因：因为ind是array([[],[],…,[]])格式的，取[0]相当于得到[],[],…,[]，取[1:]表示不要第1个，因为第1个是输入样本自己。

  调用样本合成函数self.__populate，添加"__"（2个下划线）表示是私有的，不能被外部调用。

  最后返回合成的样本self.synthetic即可。

构建合成样本函数

def __populate(self, N, i, nnarray):# 按照倍数N做循环for j in range(N):# 随机抽取1～k之间的一个整数，即选择k近邻中的一个样本用于合成数据nn = random.randint(0, self.k-1)# 计算差值diff = self.samples[nnarray[nn]] - self.samples[i]# 随机生成一个0～1之间的数gap = random.uniform(0,1)# 合成的新样本放入数组self.syntheticself.synthetic[self.newindex] = self.samples[i] + gap*diff# self.newindex加1， 表示已合成的样本又多了1个self.newindex += 1

合成样本函数__populate按照倍数N进行循环，首先生成用于挑选近邻的1～k之间的一个随机整数nn。

接着用下面的运算合成样本：
$${\mathbf{x}}_{合成}=\mathbf{x}+rand(0,1)\ast ({\mathbf{x}}_{近邻}-\mathbf{x})$$
其中，${\mathbf{x}}_{合成}$表示最终合成的一个样本，

​ $\mathbf{x}$表示输入的一个少数类样本，

​ ${\mathbf{x}}_{近邻}$表示被选中的$x$的一个近邻样本，

​ $rand(0,1)$是0~1之间的一个随机数。

最后，合成的样本${\mathbf{x}}_{合成}$都放入数组synthetic，这样就完成了一个合成样本。

newindex加1，表示已合成的样本又多了1个，合成样本函数__populate到此就执行结束了。

SMOTE算法的完整代码

下面是整合的SMOTE算法代码：

import random
from sklearn.neighbors import NearestNeighbors
import numpy as npclass Smote(object):"""SMOTE algorithm implementation.Parameters----------samples : {array-like}, shape = [n_samples, n_features]Training vector, where n_samples in the number of samples andn_features is the number of features.N : int, optional (default = 50)Parameter N, the percentage of n_samples, affects the amount of final synthetic samples，which calculated by floor(N/100)*T.k : int, optional (default = 5)Specify the number for NearestNeighbors algorithms.r : int, optional (default = 2)Parameter for sklearn.neighbors.NearestNeighbors API.When r = 1, this is equivalent to using manhattan_distance (l1), and euclidean_distance (l2) for r = 2. For arbitrary p, minkowski_distance (l_r) is used.Examples-------->>> samples = np.array([[3,1,2], [4,3,3], [1,3,4],[3,3,2], [2,2,1], [1,4,3]])>>> smote = Smote(N=200)>>> synthetic_points = smote.fit(samples)>>> print(synthetic_points)[[3.31266454 1.62532908 2.31266454][2.4178394  1.5821606  2.5821606 ][3.354422   2.677211   2.354422  ][2.4169074  2.2084537  1.4169074 ][1.86018171 2.13981829 3.13981829][3.68440949 3.         3.10519684][2.22247957 3.         2.77752043][2.3339721  2.3339721  1.3339721 ][3.31504371 2.65752185 2.31504371][2.54247589 2.54247589 1.54247589][1.33577795 3.83211103 2.83211103][3.85206355 3.04931215 3.        ]]"""def __init__(self, N=50, k=5, r=2):# 初始化self.N, self.k, self.r, self.newindexself.N = Nself.k = k# self.r是距离决定因子self.r = r# self.newindex用于记录SMOTE算法已合成的样本个数self.newindex = 0# 构建训练函数def fit(self, samples):# 初始化self.samples, self.T, self.numattrsself.samples = samples# self.T是少数类样本个数，self.numattrs是少数类样本的特征个数self.T, self.numattrs = self.samples.shape# 查看N%是否小于100%if(self.N < 100):# 如果是，随机抽取N*T/100个样本，作为新的少数类样本np.random.shuffle(self.samples)self.T = int(self.N*self.T/100)self.samples = self.samples[0:self.T,:]# N%变成100%self.N = 100# 查看从T是否不大于近邻数kif(self.T <= self.k):# 若是，k更新为T-1self.k = self.T - 1# 令N是100的倍数N = int(self.N/100)# 创建保存合成样本的数组self.synthetic = np.zeros((self.T * N, self.numattrs))# 调用并设置k近邻函数neighbors = NearestNeighbors(n_neighbors=self.k+1, algorithm='ball_tree', p=self.r).fit(self.samples)# 对所有输入样本做循环for i in range(len(self.samples)):# 调用kneighbors方法搜索k近邻nnarray = neighbors.kneighbors(self.samples[i].reshape((1,-1)),return_distance=False)[0][1:]# 把N,i,nnarray输入样本合成函数self.__populateself.__populate(N, i, nnarray)# 最后返回合成样本self.syntheticreturn self.synthetic# 构建合成样本函数def __populate(self, N, i, nnarray):# 按照倍数N做循环for j in range(N):# attrs用于保存合成样本的特征attrs = []# 随机抽取1～k之间的一个整数，即选择k近邻中的一个样本用于合成数据nn = random.randint(0, self.k-1)# 计算差值diff = self.samples[nnarray[nn]] - self.samples[i]# 随机生成一个0～1之间的数gap = random.uniform(0,1)# 合成的新样本放入数组self.syntheticself.synthetic[self.newindex] = self.samples[i] + gap*diff# self.newindex加1， 表示已合成的样本又多了1个self.newindex += 1

示例代码

给出一个使用上面编写的SMOTE算法的示例代码：

samples = np.array([[3,6], [4,3], [6,2],[7,4], [5,5], [2,2]])smote = Smote(N=325)
synthetic_points = smote.fit(samples)
print(synthetic_points)

输出为

[[3.6772233  3.26039213][3.32253148 3.07631863][3.95208383 5.02871888][5.47449381 2.52162858][3.28228767 4.74045287][5.53021385 2.74717938][6.16006835 2.71718173][5.80286476 2.10257375][5.02200271 4.32244709][5.69356263 4.16131891][4.79089496 6.54151207][6.87175337 5.08710904][6.84896105 4.91819998][3.63517092 6.96608194][4.64573998 4.69470987][2.46294632 6.11277869][2.11006928 4.29020096][2.17647179 6.66435637]]

注意，N=225，也就是希望最终生成的样本量是原样本的225%，但结果只有200%，这是因为算法限定了生成的样本量必须是原样本量的倍数，并且是向下取整，225%向下取整就是200%，这在步骤4中有相应的说明。

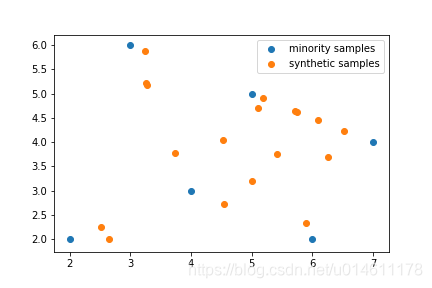
下面画出少数类样本和SMOTE合成样本的散点图：

import matplotlib.pyplot as pltplt.scatter(samples[:,0], samples[:,1])
plt.scatter(synthetic_points[:,0], synthetic_points[:,1])
plt.legend(["minority samples", "synthetic samples"])

关于SMOTE算法原论文，有一个矛盾的地方，在伪代码的合成样本函数populate中，对于样本的每个特征，$rand(0,1)$都重新生成，注意看下面伪代码红框框住的地方：

但是，在论文中给的说明SMOTE算法的例子里面，却没有说针对每个特征生成一个随机数。

究竟怎样才是对的呢？

我们参考SMOTE算法的变体Borderline-SMOTE的论文看法：

画红线的这句话就表明不是每个特征都生成一个随机数，所以伪代码那块并不正确。

Borderline-SMOTE的论文Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning链接：https://sci2s.ugr.es/keel/pdf/algorithm/congreso/2005-Han-LNCS.pdf