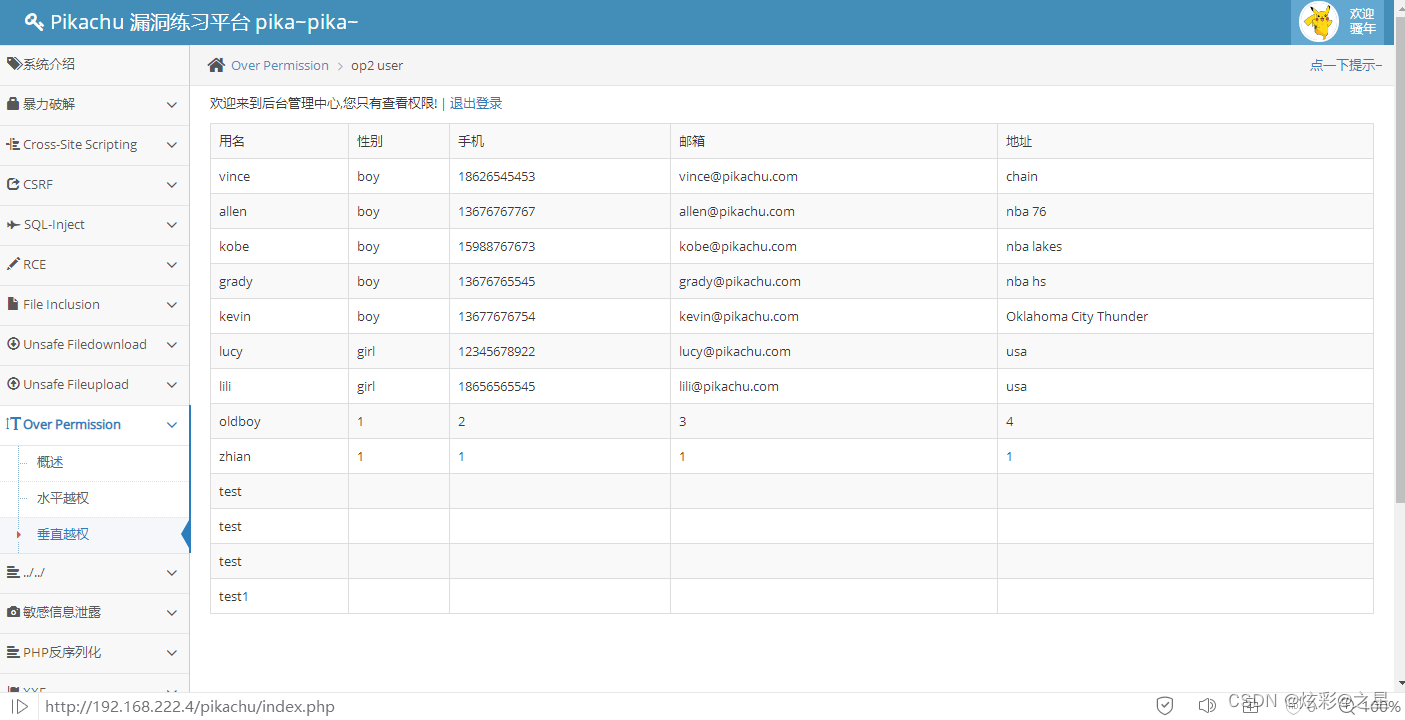
计算Hash冲突的概率
虽然已经很多可以选择的Hash函数,但创建一个好的Hash函数仍然是一个活跃的研究领域。一些Hash函数是快的,一些是慢的,一些Hash值均匀地分布在值域上,一些不是。对于我们的目的,让我们假设这个Hash函数是非常好的。它的Hash值均匀地分布在值域上。
在这种情况下,对于一个输入集合生成的Hash值是非常像生成一个随机数集合。我们的问题转化为如下:
给K个随机值,非负而且小于N,他们中至少有个相等的概率是多少?
实际上我们求这个问题的对立问题更加简单:他们都不相同的概率是多少?无论这个对立问题的结果是多少,我们用1减去对立问题的结果就得到原问题的结果。
对于一个值域为N的Hash值,假设你已经挑选出一个值。之后,剩下N-1个值是不同于第一个值的,因此,对于第二次随机生成不同第一个数的概率为N/N-1.
简而言之,有N个不同的数,你第一次挑选出某个,然后继续从N个数中挑选,那只要不是选到和第一次一样的那个数一样就不一样喽,所以概率为N-1/N。
之后就是第三次挑选,第三次挑选出的第三个数要求不同于前两个数,所以概率就为N-1/N*N-2/N.
一般的,随机生成K个数,他们都不相同的概率为: 
计算机中,对于K很大的时候计算很麻烦,幸运的是,上面的表达式近似于