hash碰撞的概率推导（生日攻击生日问题）

article/2025/11/11 12:22:09

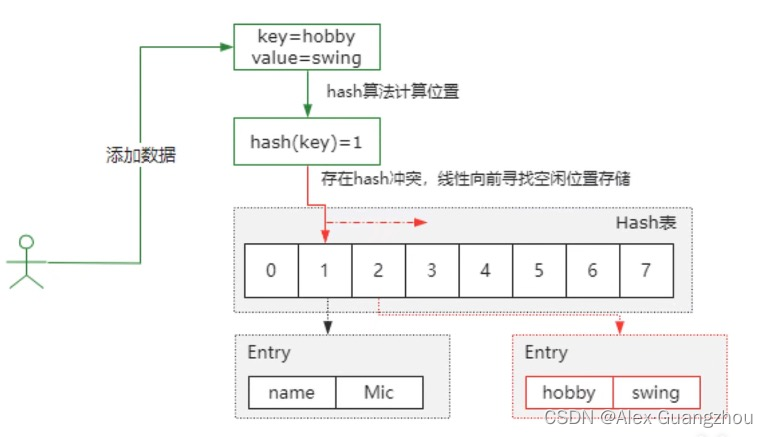
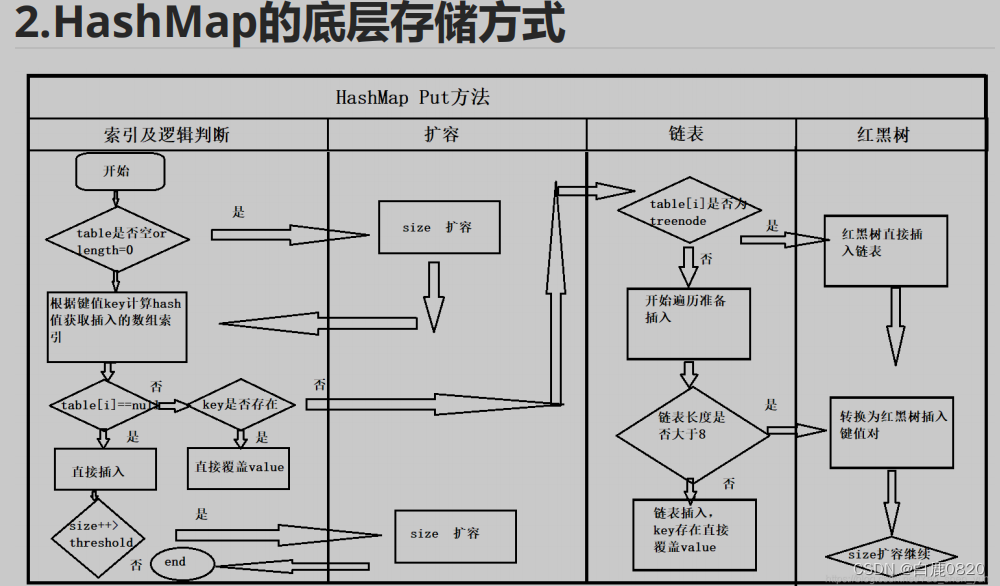
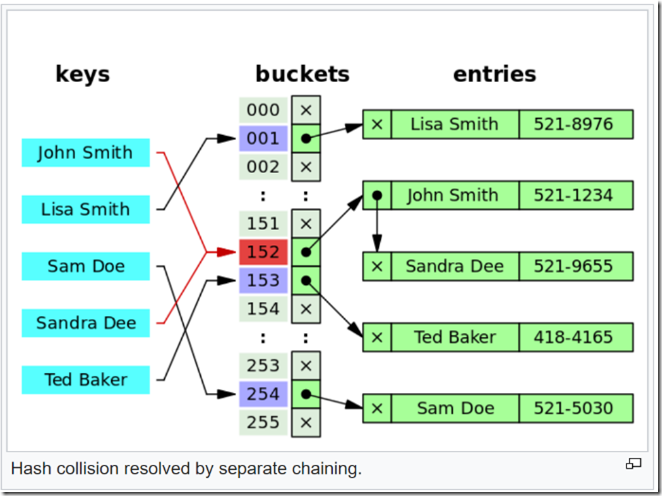
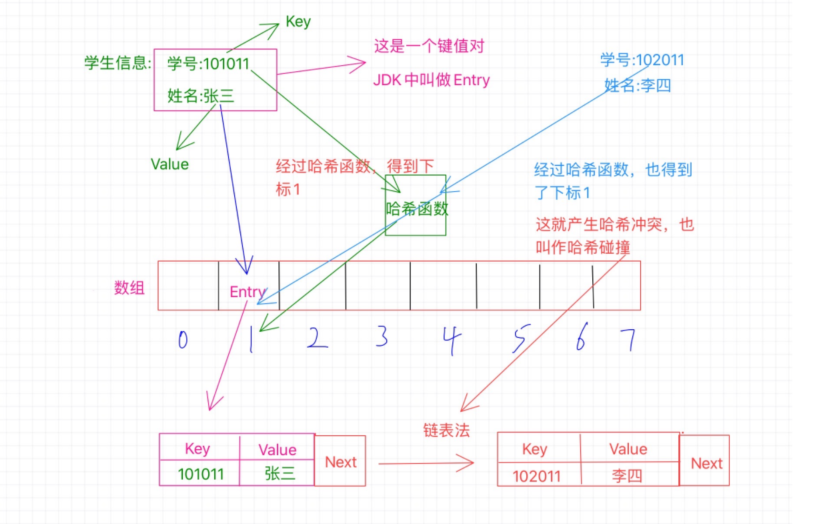
1.关于hash碰撞

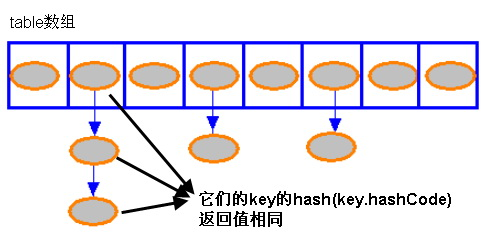
哈希碰撞是指，两个不同的输入得到了相同的输出；

hash碰撞不可避免，hash算法是把一个无限输入的集合映射到一个有限的集合里，必然会发生碰撞；

2.碰撞概率的问题描述的其他形式

n个球，（可重复的）随机放入k个桶里，至少有两个球在同一个桶里的概率；
给K个随机值，非负而且小于n，他们中至少有2个相等的概率；

3.碰撞概率的取决因素

hash碰撞的概率取决于两个因素（k, n 同上述）

hash的取值空间 k
hash的计算次数 n

4.hash碰撞概率的数学原型：生日问题

即：一个班级需要有多少人，才能保证每个同学的生日都不一样？

结果：当一个班级有7人时，至少两人生日相同的概率在5%；

当一个班级有23人时，至少两人生日相同的概率就达到了50%；

当一个班级有50人时，至少两人生日相同的概率就达到了97%；

5.生日问题概率推导

要求一个班级n个人，至少两个人生日相同的概率 Pa

可以先求每个人生日都不同的概率 Pb

进而转换为：一个空的房间里，第一个人进去与其他人不同的概率（1-0）；第二个人进入房间与其他人不同的概率（1- 1/365）；第三个人进去与其他人不同的概率（1-2/365）… 以此类推，直到最后一个人进入房间与其他人不同的概率（1-n/365）

得：
$(1-\frac{0}{365})\cdot(1-\frac{1}{365})\cdot(1-\frac{2}{365})\cdot\cdot\cdot(1-\frac{n-1}{365})\tag{1}$
进而：
$(\frac{365-0}{365})\cdot(\frac{365-1}{365})\cdot(\frac{365-2}{365})\cdot\cdot\cdot(\frac{365-(n-1)}{365})\tag{2}$
化简：
$\frac{365!}{365^n(365-n)!}\tag{3}$
故至少两人生日概率相同Pa为：
$1-\frac{365!}{365^n(365-n)!}\tag{4}$
(4)式即为所求的公式，但是这个公式不便于计算，x趋于0时，根据泰勒公式：
$\lim_{x \to 0}e^x = 1+x+\frac{1}{2}x^2+\frac{1}{6}x^3+\frac{1}{24}x^4\cdot\cdot\cdot\tag{5}$

近似的有：
$e^x \approx 1+x\tag{6}$

观察（1）式，用（6）式代入得：
$\approx (e^{-\frac{0}{365}})\cdot(e^{-\frac{1}{365}})\cdot(e^{-\frac{2}{365}})\cdot\cdot\cdot(e^{-\frac{n-1}{365}})\tag{7}$
化简：
$\approx e^{-\frac{n(n-1)}{2\cdot365}}\tag{8}$
故：
$\approx 1 - e^{-\frac{n(n-1)}{2\cdot365}}\tag{9}$

6.hash碰撞概率推导

要求给K个随机值，非负而且小于n，他们中至少有2个相等的概率 Pa

由上述推导不难看出：
$1-\frac{k!}{k^n(k-n)!}\tag{10}$
且由泰勒展开式，近似得：
$\approx 1 - e^{-\frac{n(n-1)}{2\cdot k}}\tag{11}$

7.python作图

在生日概率问题中，k取365，做概率 Pa 关于班级人数n的函数图像：

准确表达式图像(4)式（acc）

近似表达式图像(9)式（fit）

在这里插入图片描述

代码：

import matplotlib.pyplot as plt
import numpy as np
import mathdef f_accurate(k, n):if n <= 0 or k <= 0:return -1if n > k:return 1var1 = 1for i in range(k - (n - 1), k + 1):var1 *= (i / k)return 1 - var1def f_fit(k, n):if n <= 0 or k <= 0:return -1if n > k:return 1var1 = (-1) * n * (n - 1) / (2 * k)var2 = math.pow(math.e, var1)return 1 - var2def f_plot_var_n(k, n):acc = []fit = []for i in range(1, n):acc.append(f_accurate(k, i))fit.append(f_fit(k, i))arr = np.array(range(1, n))acc = np.array(acc)fit = np.array(fit)plt.title("crash rate k = {}".format(k))plt.xlabel("n number")plt.ylabel("p(n) rate")plt.plot(arr, acc, color='blue', label='acc')plt.plot(arr, fit, color='red', label='fit')plt.legend()plt.show()def f_plot_var_k(k, n):acc = []fit = []for i in range(1, k):acc.append(f_accurate(i, n))fit.append(f_fit(i, n))arr = np.array(range(1, k))acc = np.array(acc)fit = np.array(fit)plt.title("crash rate n = {}".format(n))plt.xlabel("k number")plt.ylabel("p(k) rate")plt.plot(arr, acc, color='blue', label='acc')plt.plot(arr, fit, color='red', label='fit')plt.legend()plt.show()if __name__ == '__main__':k_value = 365n_value = 365# k_value = 10000# n_value = 100f_plot_var_n(k_value, n_value)# f_plot_var_k(k_value, n_value)

可以看出近似表达式与准确表达式相差不大；

碰撞概率在n=23时，已经达到了50%，而取值空间为[0,365]

这对hash取值空间长度的取舍有参考意义；