/*
* 克鲁斯卡尔算法
* 1.用来求加权连通图的最小生成树的算法
* 2.思想:按照权值从小到大的顺序,选择n-1条边,并保证这n-1条边不构成回路
* 3.先构造一个只含n个顶点的森林,依权值从小到大从连通网中选择边加入到森林中
* 并使森林不产生回路,直至森林变成一棵树
*
* 终点:将所有顶点从小到大排序后,某个顶点的终点就是与它连通的最大顶点
* 判断回路:加入边的两个顶点不能都指向同一个终点,否则构成回路
*
* 应用——修路问题
*
*/
public class Kruskal {
private int edgeNum;//边的个数
private char[] vertexs;//顶点数组
private int[][] matrix;//邻接矩阵
private static final int INF = Integer.MAX_VALUE;//使用INF表示两个顶点不连通
public static void main(String[] args) {
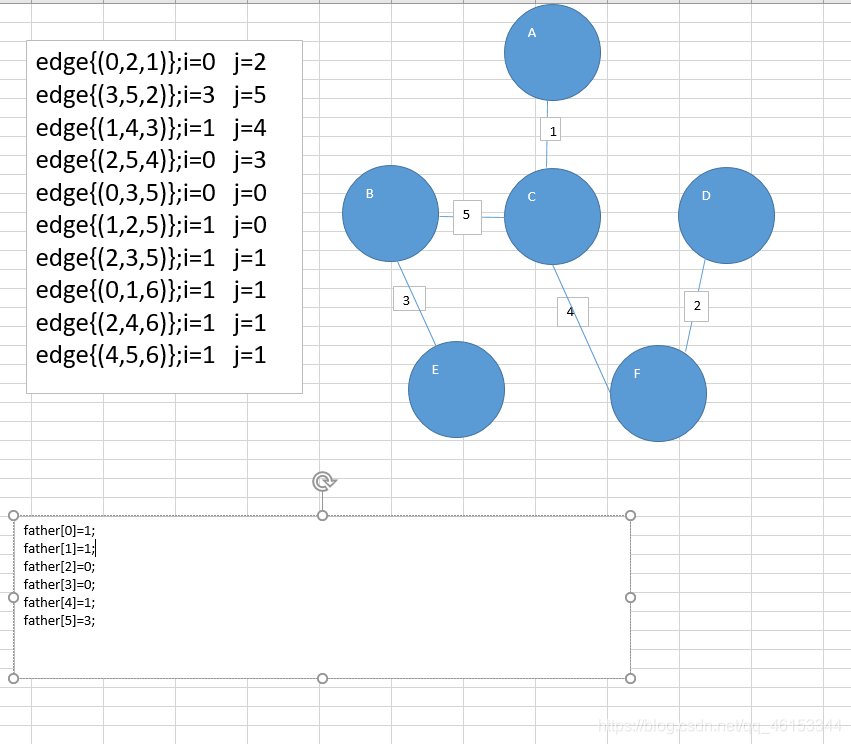
char[] vertexs = {'A','B','C','D','E','F','G'};
//邻接矩阵
int[][] matrix = {
{0 ,12 ,INF,INF,INF,16 ,14 },
{12 ,0 ,10 ,INF,INF,7 ,INF},
{INF,10 ,0 ,3 ,5 ,6 ,INF},
{INF,INF,3 ,0 ,4 ,INF,INF},
{INF,INF,5 ,4 ,0 ,2 ,8 },
{16 ,7 ,6 ,INF,2 ,0 ,9 },
{14 ,INF,INF,INF,8 ,9 ,0 }};
//创建对象实例
Kruskal kruskal = new Kruskal(vertexs, matrix);
//输出
kruskal.print();
kruskal.kruskal();
}
//构造器
public Kruskal(char[] vertexs,int[][] matrix) {
//初始化顶点数和边数
int vlen = vertexs.length;
//初始化顶点(复制拷贝)
this.vertexs = new char[vlen];
for(int i = 0;i < vertexs.length;i++) {
this.vertexs[i] = vertexs[i];
}
//this.vertexs = vertexs;
//初始化边(复制拷贝)
this.matrix = new int[vlen][vlen];
for(int i = 0;i < vlen;i++) {
for(int j = 0;j < vlen;j++) {
this.matrix[i][j] = matrix[i][j];
}
}
//统计边
for(int i = 0;i < vlen;i++) {
for(int j = i+1;j < vlen;j++) {
if (this.matrix[i][j] != INF) {
edgeNum++;
}
}
}
}
//克鲁斯卡尔算法
public void kruskal() {
int index = 0;//表示最后结果数组的索引
int[] ends = new int[edgeNum];//保存已有最小生成树中每个顶点的终点
//创建结果数组,保存最小生成树
EData[] res = new EData[edgeNum];
//获取图中所有边的集合
EData[] edges = getEdges();
//按照边权值进行排序
sortEdges(edges);
//遍历edges数组,将边添加到最小生成树,判断是否构成回路,如不构成加入到res
for(int i = 0;i < edgeNum;i++) {
//获取第i条边的一个点
int p1 = getPosition(edges[i].start);
//获取第i条边的另一个点
int p2 = getPosition(edges[i].end);
//获取p1,p2在已有最小生成树的终点
int m = getEnd(ends, p1);
int n = getEnd(ends, p2);
//判断是否构成回路
if (m != n) {//没构成
ends[m] = n;//设置m在已有最小生成树的终点
res[index++] = edges[i];//加入到res
}
}
//统计并输出最小生成树
System.out.println("最小生成树为");
for(int i = 0;i < index;i++) {
System.out.println(res[i]);
}
}
//输出邻接矩阵
public void print() {
System.out.println("邻接矩阵为");
for(int i = 0;i < vertexs.length;i++) {
for(int j = 0;j < vertexs.length;j++) {
System.out.printf("%8d\t",matrix[i][j]);
}
System.out.println();
}
}
//对边权值进行排序(冒泡)
//edges:边的集合
private void sortEdges(EData[] edges) {
for(int i = 0;i < edges.length - 1;i++) {
for(int j = 0;j < edges.length - 1 - i;j++) {
if (edges[j].weight > edges[j+1].weight) {
EData temp = edges[j];
edges[j] = edges[j+1];
edges[j+1] = temp;
}
}
}
}
//ch:顶点值,返回顶点对应下标,找不到返回-1
private int getPosition(char ch) {
for(int i = 0;i < vertexs.length;i++) {
if (vertexs[i] == ch) {//找到
return i;
}
}
return -1;
}
//获取图中的边(通过邻接矩阵),放入EData[]数组,遍历该数组
private EData[] getEdges() {
int index = 0;
EData[] edges = new EData[edgeNum];
for(int i = 0;i < vertexs.length;i++) {
for(int j = i+1;j < vertexs.length;j++) {
if (matrix[i][j] != INF) {
edges[index++] = new EData(vertexs[i], vertexs[j], matrix[i][j]);
}
}
}
return edges;
}
//获取下标为i的顶点的终点
//ends:顶点终点的集合,i:顶点对应下标
private int getEnd(int[] ends,int i) {
while(ends[i] != 0) {
i = ends[i];
}
return i;
}
}
//创建类EData,对象实例表示一条边
class EData{
char start;//边的一个点
char end;//边的另一个点
int weight;//边的权值
//构造器
public EData(char start,char end,int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
//重新toString,输出边信息
@Override
public String toString() {
return "EData [<" + start + ", " + end + ">=" + weight + "]";
}
}
import java.util.Arrays;
/*
* 迪杰斯特拉算法
* 1.迪杰斯特拉算法是典型最短路径算法,用于计算一个结点到其他结点的最短路径
* 2.主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止
*
* 算法过程
* 设置出发顶点v,顶点集合V{v1,v2,...},v到V中各顶点的距离构成距离集合Dis,
* Dis{d1,d2...},Dis集合记录v到各顶点的距离(到自身可看成0,v到vi距离对应为di)
*
* 1.从Dis中选择最小的di并移出Dis集合,同时移出V集合中对应的顶点vi,此时v到vi即为最短路径
* 2.更新Dis集合:比较v到V集合中顶点的距离值,与v通过vi到V集合中顶点的距离值,保留值较小的一个
* (同时更新顶点前驱为vi,表明是通过vi到达的)
* 3.重复执行1,2,直到最短路径顶点为目标顶点时结束
*
*
*
* 应用——最短路径问题
*
*/
public class Dijkstra {
public static void main(String[] args) {
char[] vertex = {'A','B','C','D','E','F','G'};
//邻接矩阵
int[][] matrix = new int[vertex.length][vertex.length];
final int N = 65535;//表示不可连接
matrix[0] = new int[] {N,5,7,N,N,N,2};
matrix[1] = new int[] {5,N,N,9,N,N,3};
matrix[2] = new int[] {7,N,N,N,8,N,N};
matrix[3] = new int[] {N,9,N,N,N,4,N};
matrix[4] = new int[] {N,N,8,N,N,5,4};
matrix[5] = new int[] {N,N,N,4,5,N,6};
matrix[6] = new int[] {2,3,N,N,4,6,N};
//创建Graph对象
Graph graph = new Graph(vertex, matrix);
//输出邻接矩阵
graph.showGraph();
//测试迪杰斯特拉算法
graph.dsj(6);
graph.showDijkstra();
}
}
class Graph{
private char[] vertex;//顶点数组
private int[][] matrix;//邻接矩阵
private VisitedVertex visitedVertex;//已访问顶点集合
//构造器
public Graph(char[] vertex,int[][] matrix) {
this.vertex = vertex;
this.matrix = matrix;
}
//显示结果
public void showDijkstra() {
visitedVertex.show();
}
//显示图
public void showGraph() {
for(int[] link : matrix) {
System.out.println(Arrays.toString(link));
}
}
//迪杰斯特拉算法
//index:出发顶点对应的下标
public void dsj(int index) {
visitedVertex = new VisitedVertex(vertex.length, index);
update(index);//更新index顶点到周围顶点的距离和前驱顶点
for(int j = 1;j < vertex.length;j++) {
index = visitedVertex.updateArr();//选择并返回新的访问结点
update(index);//更新index顶点到周围顶点的距离和前驱顶点
}
}
//更新index下标顶点到各个顶点的距离和前驱顶点
private void update(int index) {
int len = 0;
//遍历邻接矩阵index行
for(int j = 0;j < matrix[index].length;j++) {
//len:出发顶点到index顶点的距离 + 从index顶点到j顶点的距离
len = visitedVertex.getDis(index) + matrix[index][j];
//如果顶点j没有被访问且len小于出发顶点到j顶点的距离,就更新
if (!visitedVertex.in(j) && len < visitedVertex.getDis(j)) {
visitedVertex.updatePre(j, index);//更新j顶点的前驱为index顶点
visitedVertex.updateDis(j, len);//更新出发顶点到j顶点的距离
}
}
}
}
//已访问顶点集合
class VisitedVertex{
//记录各个顶点是否访问过(1表示访问,0表示未访问)
public int[] already_arr;
//每个下标对应的值为前一个顶点下标
public int[] pre_visited;
//记录出发顶点到其他所有顶点的距离
public int[] dis;
//构造器
//lenght:顶点个数,index:出发顶点对应的下标
public VisitedVertex(int lenght,int index) {
this.already_arr = new int[lenght];
this.pre_visited = new int[lenght];
this.dis = new int[lenght];
//初始化dis,设置出发顶点到自身的距离为0,其他为65535
Arrays.fill(dis, 65535);
this.dis[index] = 0;
this.already_arr[index] = 1;//设置出发顶点被访问过
}
//判断index是否被访问过,如果访问过返回true
public boolean in(int index) {
return already_arr[index] == 1;
}
//更新出发顶点到index顶点的距离
public void updateDis(int index,int len) {
dis[index] = len;
}
//更新顶点前驱为index结点
public void updatePre(int pre,int index) {
pre_visited[pre] = index;
}
//返回出发顶点到index顶点的距离
public int getDis(int index) {
return dis[index];
}
//继续选择并返回新的访问顶点
public int updateArr() {
int min = 65535;
int index = 0;
for(int i = 0;i < already_arr.length;i++) {
if (already_arr[i] == 0 && dis[i] < min) {
min = dis[i];
index = i;
}
}
//更新index顶点被访问过
already_arr[index] = 1;
return index;
}
//显示最后结果
public void show() {
System.out.println("==============================");
//输出already_arr
for(int i : already_arr) {
System.out.print(i + " ");
}
System.out.println();
//输出pre_visited
for(int i : pre_visited) {
System.out.print(i + " ");
}
System.out.println();
//输出dis
for(int i : dis) {
System.out.print(i + " ");
}
}
}








![提问的艺术[转]](http://tieba.github.io/images/howtoask.png)