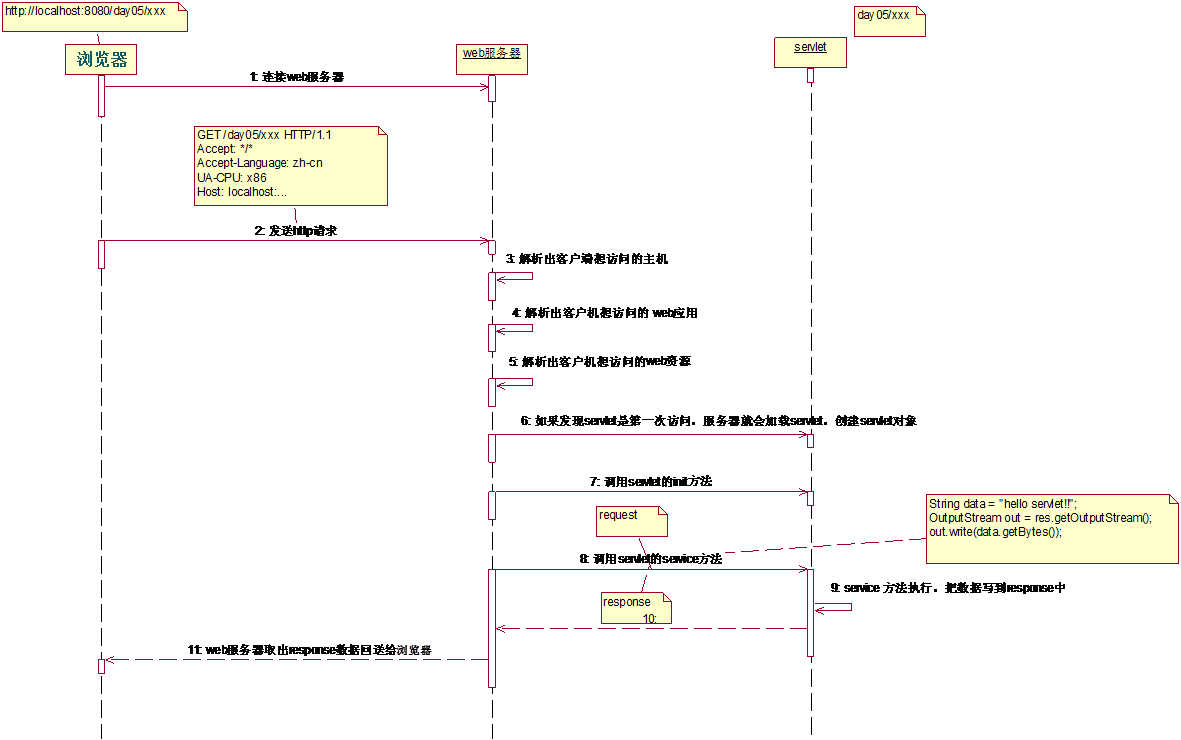
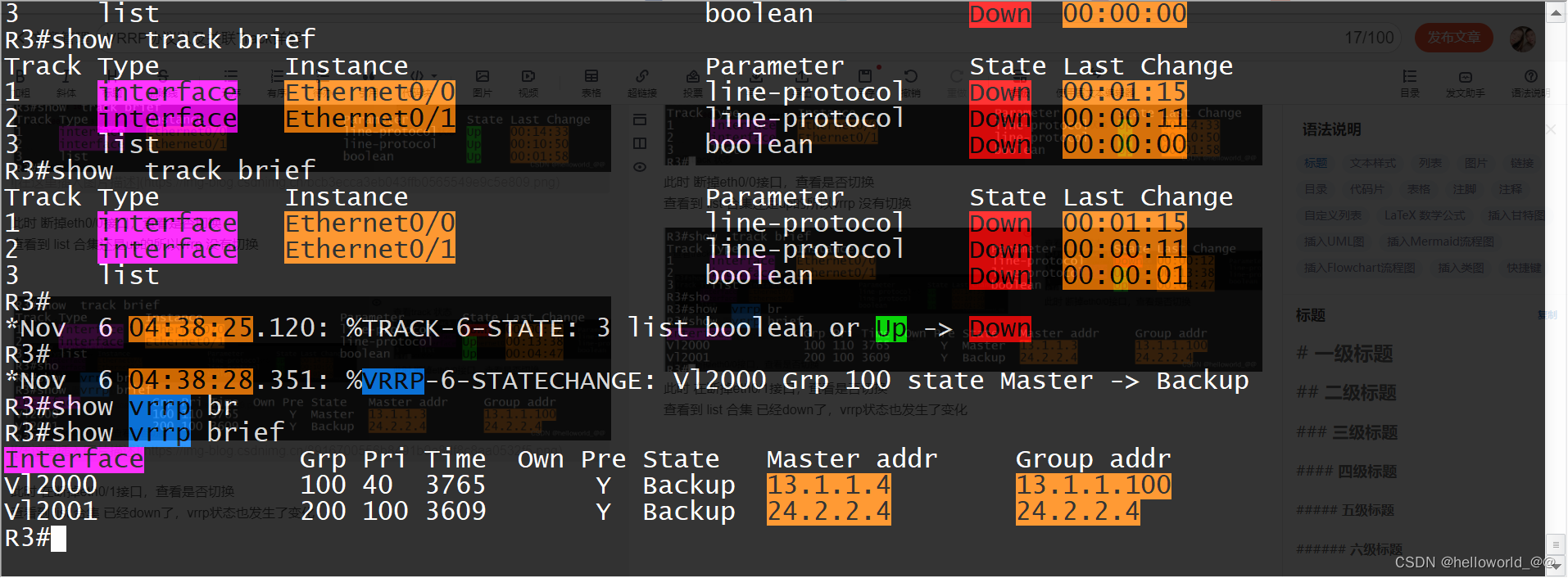
Kruskal算法

Kruskal算法是一种用来查找最小生成树的算法，由Joseph Kruskal在1956年发表。用来解决同样问题的还有Prim算法和Boruvka算法等。三种算法都是贪心算法的应用。

概念解释

Kruskal算法定义：**先构造一个只含 n 个顶点、而边集为空的子图，把子图中各个顶点看成各棵树上的根结点，之后，从网的边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，即把两棵树合成一棵树，反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直到森林中只有一棵树，也即子图中含有 n-1 条边为止。

最小生成树定义：一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。（可以由Kruskal算法或者prim算法求出来）

执行步骤：：
第一步：在带权连通图中，将边的权值排序；
第二步：判断是否需要选择这条边（此时图中的边已按权值从小到大排好序）。判断的依据是边的两个顶点是否已连通，如果连通则继续下一条；如果不连通，那么就选择使其连通。
第三步：循环第二步，直到图中所有的顶点都在同一个连通分量中，即得到最小生成树。

图解Kruskal算法

首先将图中的所有的边按权值从小到大排序：
HG < (CI=GF) < (AB=CF) < GI < (CD=HI) < (AH=BC) < DE < BH < DF
接着，我们选择HG这条边，这样就将H和G这两个点加入到了已经找到的点的集合。如下图所示：

由于两个一样的权值的边存在，所以就可以随便选一条，但是需要做出判断。
判断的法则：
（1）当所选的边加入已找到边的集合时候，会不会形成回路。如果没有形成回路，那么就“准备”将其连通，在真正连通之前还需要做一次判断，判断这两个点是否已经加入到已找到点的集合中去了
（2）如果两个点都没有出现，则将这两个点都加入到集合中去
（3）如果其中有一个点已经出现在集合中，则将另一个没有出现过的点，加入到集合中去
（4）如果两个都有出现，则不需要加入。

以上三步不会形成回路，所以可以直接连通。

在连接IG的时候，会形成回路，所以放弃连通。
如何判断的？注意听这里是算法实现的重点：
判断两个已经连接到第三个点的点，会不会连接。

至此我们得到了一个最小生成树。所有的点都在一个连通分量上了。

注意点：排序和防止回路

排序的解决：很好解决

（1）、只能用图中有的边；
（2）、只能用掉|v|-1条边；
（3）、不能有回路。

kruskal和prim的比较：

kruskal适用于比较稀疏的图，因为他每次都是从最小的边开始查找。让森林合并为树

prim算法适用于变数比较多的图。让小树慢慢长大。

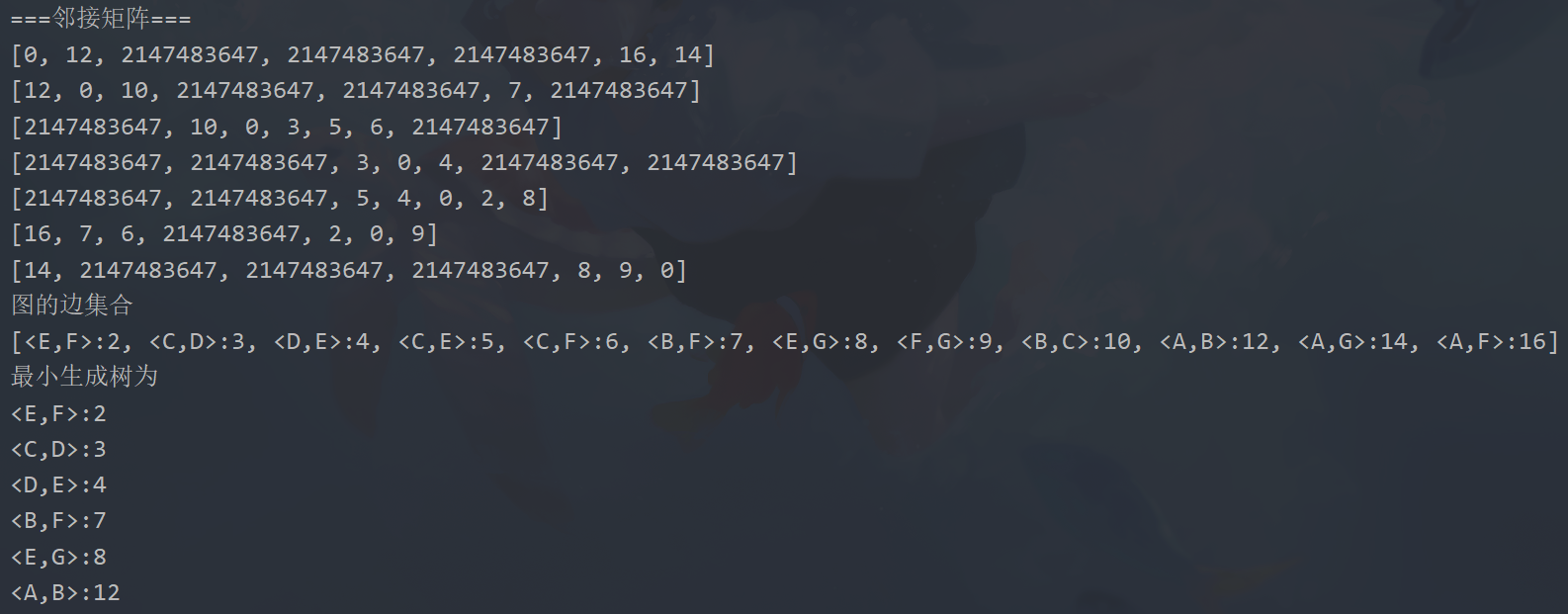
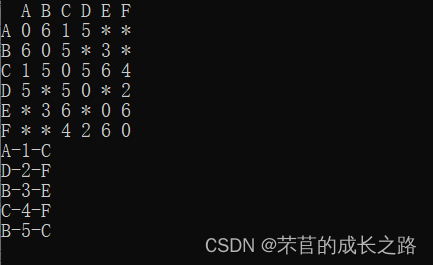
简单的例子：

public class Kruskal2 {private Edge[] edges;private int edgeSize;public Kruskal2(int edgeSize) {this.edgeSize = edgeSize;edges = new Edge[edgeSize];createEdgeKruskal();}/*** 创建边的集合，从小到大*/private void createEdgeKruskal() {
//        Edge edge0 = new Edge(6, 7, 1);
//        Edge edge1 = new Edge(5, 6, 2);
//        Edge edge2 = new Edge(2, 8, 2);
//        Edge edge3 = new Edge(0, 1, 4);
//        Edge edge4 = new Edge(2, 5, 4);
//        Edge edge5 = new Edge(6, 8, 6);
//        Edge edge6 = new Edge(7, 8, 7);
//        Edge edge7 = new Edge(2, 3, 7);
//        Edge edge8 = new Edge(1, 2, 8);
//        Edge edge9 = new Edge(0,7 , 8);
//        Edge edge10 = new Edge(3, 4, 9);
//        Edge edge11 = new Edge(4, 5, 10);
//        Edge edge12 = new Edge(1, 7, 11);
//        Edge edge13 = new Edge(3, 5, 14);
//        Edge edge14 = new Edge(4, 5, 26);Edge edge0 = new Edge(0, 3, 1);Edge edge1 = new Edge(1, 2, 2);Edge edge2 = new Edge(0,1,3);Edge edge3 = new Edge(1, 3, 5);Edge edge4 = new Edge(2, 3, 8);edges[0] = edge0;edges[1] = edge1;edges[2] = edge2;edges[3] = edge3;edges[4] = edge4;
//        edges[5] = edge5;
//        edges[6] = edge6;
//        edges[7] = edge7;
//        edges[8] = edge8;
//        edges[9] = edge9;
//        edges[10] = edge10;
//        edges[11] = edge11;
//        edges[12] = edge12;
//        edges[13] = edge13;
//        edges[14] = edge14;}/*** kruskal算法创建最小生成树*/public void createMinSpanTreeKruskal() {// 定义一个一维数组，下标为连线的起点，值为连线的终点int[] parent = new int[edgeSize];for (int i = 0; i < edgeSize; i++) {parent[i] = 0;}int sum = 0;for (Edge edge : edges) {//6, 7, 1// 找到起点和终点在临时连线数组中的最后连接点int start = find(parent, edge.start);// 6 2int end = find(parent, edge.end); // 7 8// 通过起点和终点找到的最后连接点是否为同一个点，是则产生回环if (start != end) {// 没有产生回环则将临时数组中，起点为下标，终点为值parent[start] = end;System.out.println("访问到了节点：{" + start + "," + end + "}，权值：" + edge.weight);sum += edge.weight;}}for (int i : parent) {System.out.println(i+",");}System.out.println("最小生成树的权值总和：" + sum);}/*** 获取集合的最后节点*/private int find(int parent[], int index) {
//    	System.out.println(parent[index]);while (parent[index] > 0) {index = parent[index];}return index;}/*** 连接顶点的边*/class Edge {private int start;private int end;private int weight;public Edge(int start, int end, int weight) {this.start = start;this.end = end;this.weight = weight;}}public static void main(String[] args) {Kruskal2 graphKruskal = new Kruskal2(5);graphKruskal.createMinSpanTreeKruskal();}}