什么是克鲁斯卡尔算法

在知道克鲁斯卡尔算法之前我们先来看一下什么是最小生成树。

• 最小生成树：在一个有n个结点的无向图中选出最少的边，保证所选边权相加之和最小以及该图中依然有n个结点并且n个结点连通。
• 一共有n个结点，要保证连通，至少需要n-1条边。
• 最小生成树的权值：$w(t)=\sum _{(u,v)\in t}w(u,v)$

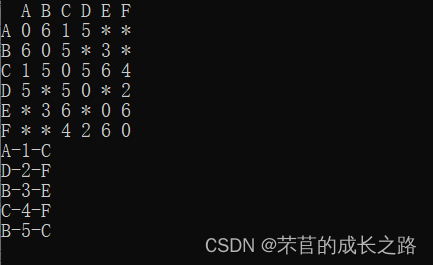
下面我们用图看一下什么是最小生成树：

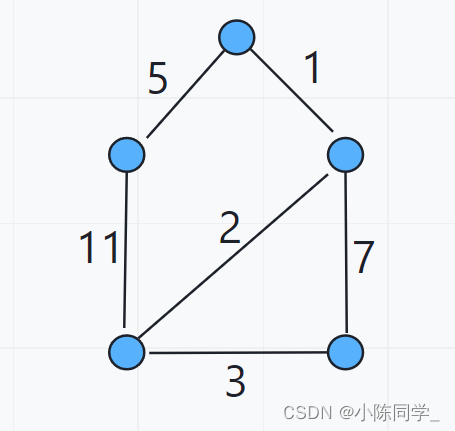
在该图中，我们留下这四条边就可以保证各个结点是连通的了，同时也保证所有边权之和最小，所以这个图的最小生成树权值为：$1+2+3+5=11$

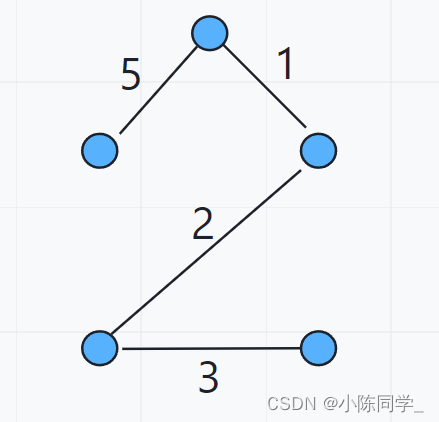
在了解了什么是最小生成树之后，我们来看克鲁斯卡尔算法是如何求最小生成树的。
思路：

1. 先按边权从小到达排序。
2. 从小到大依次看每条边，如果中途发现某一条边的所依附的点已经连通了，就直接跳过，直到n个点连通。

让我们对上面的图稍作修改作为新图模拟一遍克鲁斯卡尔算法：
（1）修改后图（此图为新图）

（2）
开始克鲁斯卡尔算法来找到第一条边

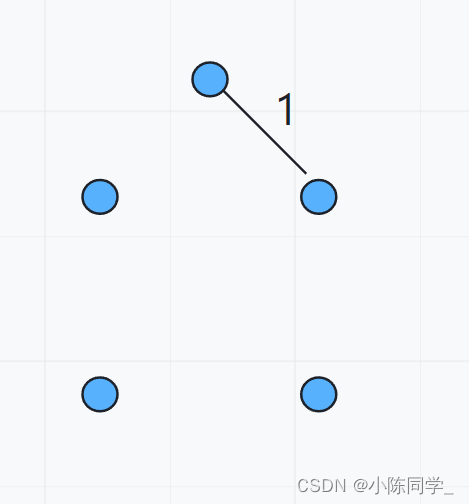
（3）
找到第二条边

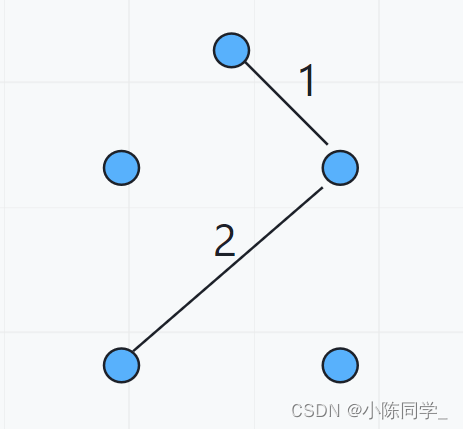
（4）
找到第三条边

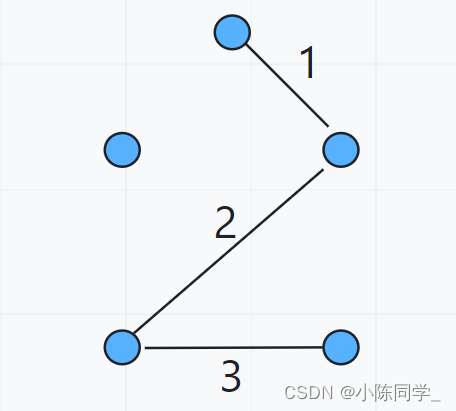
（5）
当找到第四条边时，我们发现第四条边两边所依附的点已经是连通的了，根据克鲁斯卡尔算法的思路，我们是要去掉这条边的。为什么要去掉这条边呢？ 既然这两个点已经连通了，那我们肯定是可以不选这条边的，不选这条边必然不会让结果变得更差，所以我们直接跳过这条边。

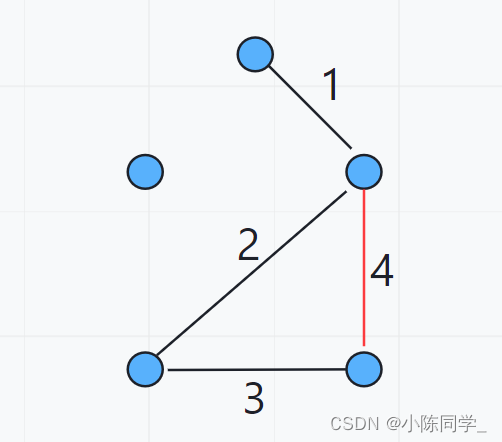
（6）
找到第五条边，找完五条边可以发现此时此刻所有的点已经连通了，最小生成树已经找到！
最小生成树的权值：$1+2+3+5=11$

核心代码（C++）

在克鲁斯卡尔算法中，习惯开一个结构体来存每条边和两边的点。

struct Edge{int a,b,w;  //a结点和b结点有一条边权为w的边bool operator<(const Edge &W)const{   //重载小于号,按w排序return w<W.w;}
}edges[N];

判断连通可以用并查集来判断，如果在同一个集合内说明已经连通。

//并查集
int find(int x){if(x!=p[x]) p[x]=find(p[x]);return p[x];
}

题目：

给定一个 $n$ 个点 $m$ 条边的无向图，图中可能存在重边和自环，边权可能为负数。

求最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible

给定一张边带权的无向图 $G=(V,E)$，其中 V 表示图中点的集合，E 表示图中边的集合，$n=|V|$，$m=|E|$。

由 $V$ 中的全部 $n$ 个顶点和 $E$ 中 $n-1$ 条边构成的无向连通子图被称为 $G$ 的一棵生成树，其中边的权值之和最小的生成树被称为无向图 $G$ 的最小生成树。

输入格式
第一行包含两个整数 $n$ 和 $m$。

接下来 m 行，每行包含三个整数 $u$,$v$,$w$，表示点 $u$ 和点 $v$ 之间存在一条权值为 $w$ 的边。

输出格式
共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

数据范围
$1\le n\le 10^5$
$1\le m\le 2\ast 10^5$
图中涉及边的边权的绝对值均不超过 1000。

输入样例：

4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4

输出样例：

6

AC代码（C++）

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;const int N=2e5+10,INF=0x3f3f3f3f;
int p[N];
int n,m;
int res;//按边排序
struct Edge{int a,b,w;bool operator<(const Edge &W)const{return w<W.w;}
}edges[N];//并查集
int find(int x){if(x!=p[x]) p[x]=find(p[x]);return p[x];
}bool kruskal(){sort(edges,edges+m);int cnt=0;  //边数for(int i=1;i<=n;i++) p[i]=i;for(int i=0;i<m;i++){int a=edges[i].a,b=edges[i].b,w=edges[i].w;a=find(a),b=find(b);if(a!=b){  //判断是否在一个集合p[a]=b;cnt++;res+=w;}}return cnt==n-1;
}int main(){int a,b,w;scanf("%d%d",&n,&m);for(int i=0;i<m;i++){scanf("%d%d%d",&a,&b,&w);edges[i]={a,b,w};}int t=kruskal();if(!t) puts("impossible");else printf("%d",res);return 0;
}