克鲁斯卡尔思路以及代码分析

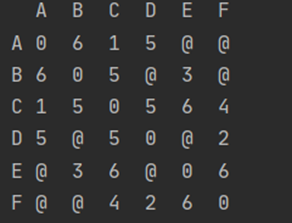
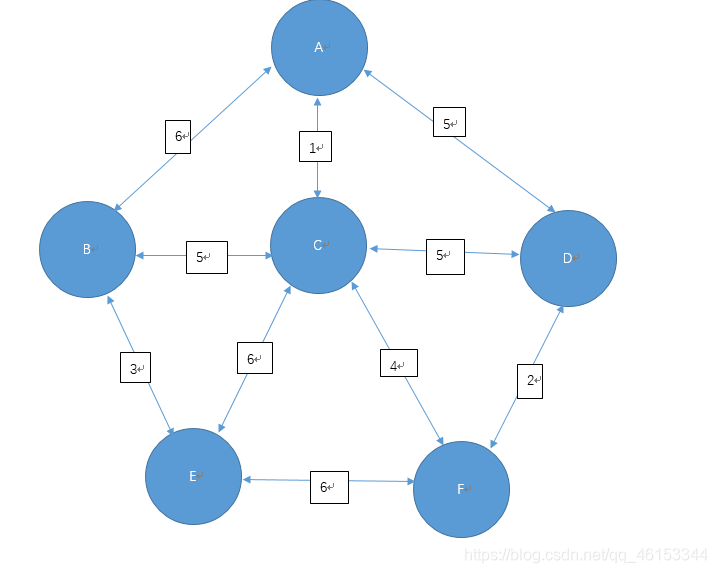
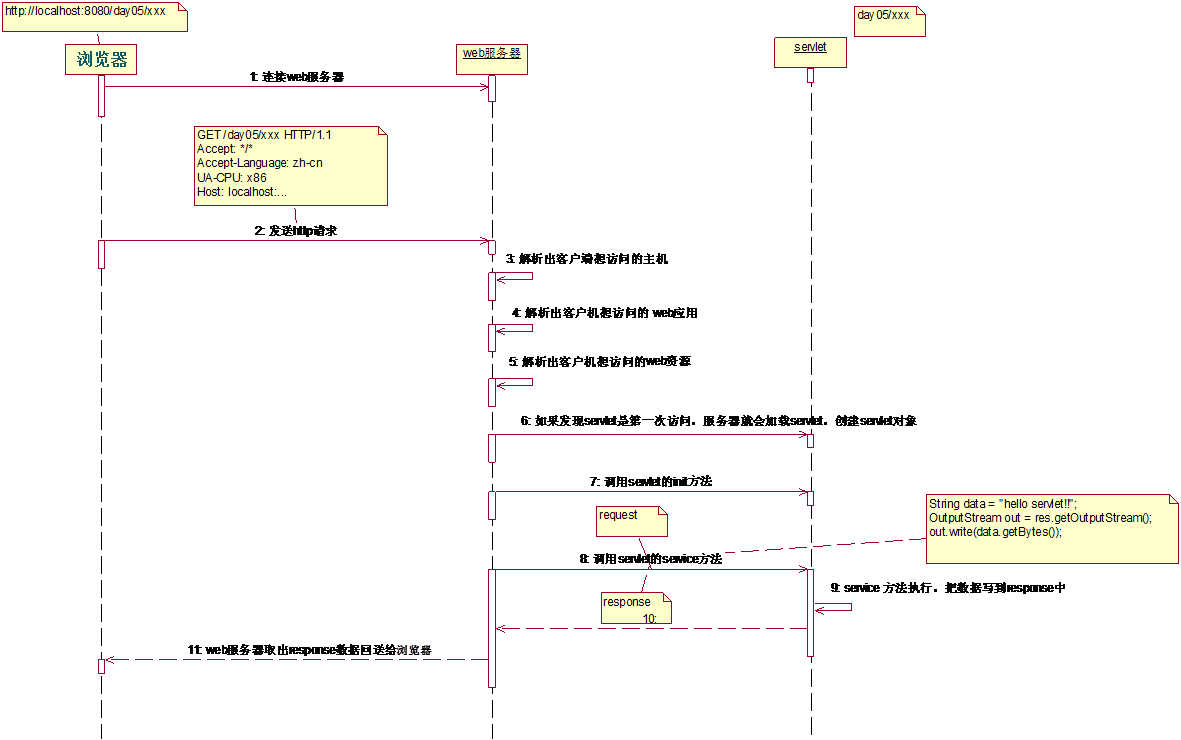
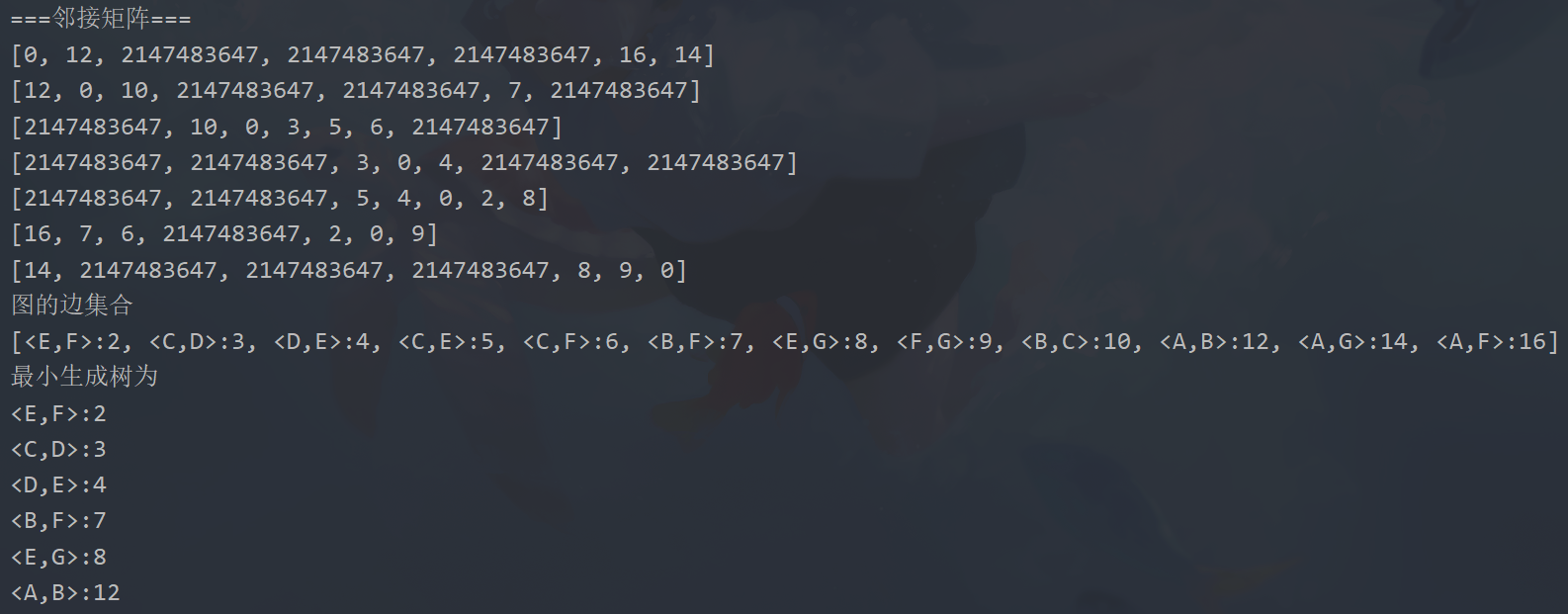
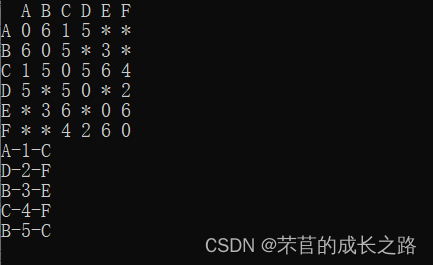
我们用邻接矩阵来表示该图，克鲁斯卡尔算法思想及找到最小边，查看是否形成回路，若形成回路则这条边不形成，若不形成回路则构成最小路径，以此类推。（思路和代码都在下方）

• 第一步edge{(0,2,1)}

• 

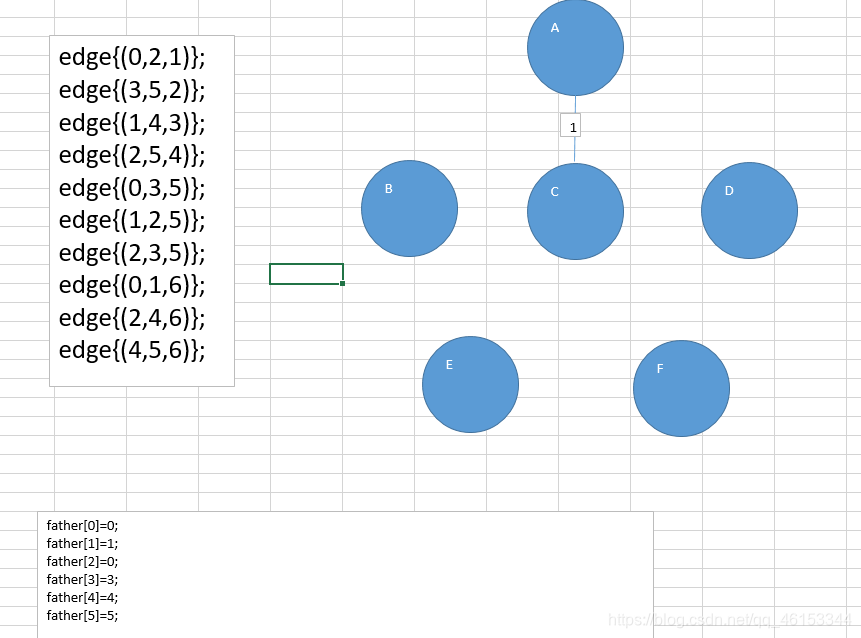
• [ ]第二步 edge{(3,5,2)}

• 

• 第三步edge{(1,4,3)}

• 

• 第四步edge{(2,5,4)}
  

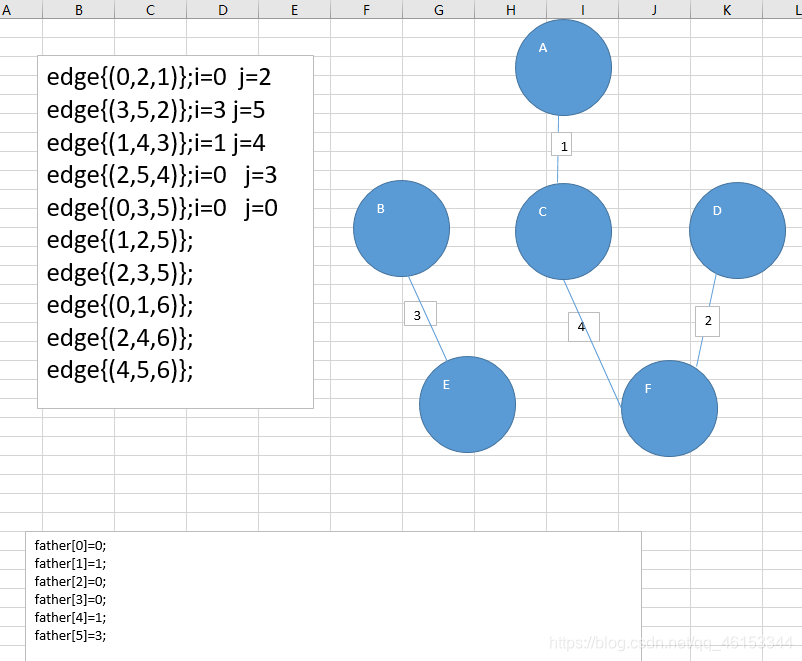
• 第五步edge{(0,3,5)}
  i==j 不添加
  

• 第六步edge{(1,2,5)}
  
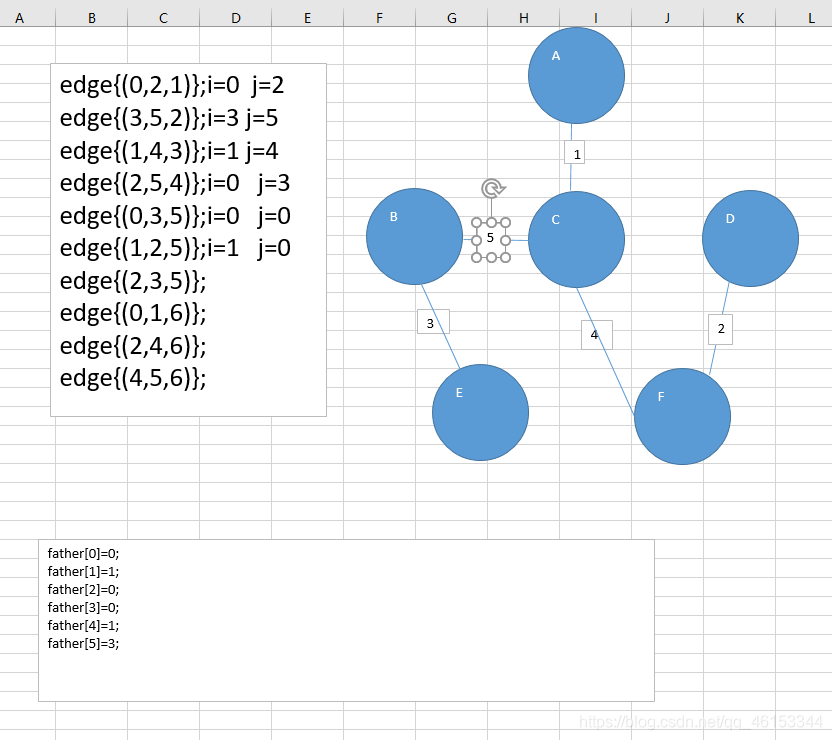
  最短路径形成，后面的思路以此类推但是都形成回路。不添加。
  

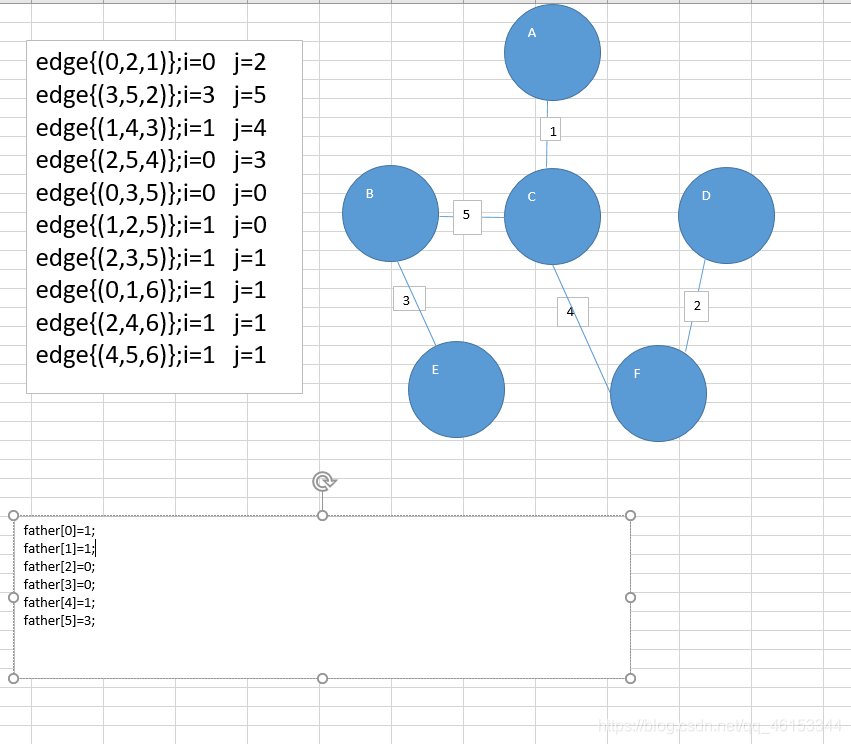
1. 创建一个Edge数组，存放邻接矩阵的有用数据

typedef struct Edge{int x;int y;int cost;//路径大小
}
int n = g->NumVertices;Edge *edge = (Edge *)malloc(sizeof(Edge) * (n*(n-1)/2));assert(edge != NULL);int k = 0;//初始化edgefor(int i=0; i<n; ++i){for(int j=i; j<n; ++j){if(g->Edge[i][j]!=0 && g->Edge[i][j]!=MAX_COST){edge[k].x = i;edge[k].y = j;edge[k].cost = g->Edge[i][j];k++;}}}

2. 对Edge中的cost排序（对图的边进行从小到大进行排序）
   排序我们直接用stdlib.h中的qsort快速排序方法

int cmp(const void*a, const void *b)
{return (*(Edge*)a).cost - (*(Edge*)b).cost;
}
qsort(edge,k,sizeof(Edge),cmp);

3.创建father数组用来存放父节点
father数组用来存放各个节点的父节点，如果两个节点的father节点相同则不形成路径。（避免形成回路）

int *father = (int*)malloc(sizeof(int) * n);
assert(father != NULL);
for(i=0; i<n; ++i)
{father[i] = i;
}

4.克鲁斯卡尔算法核心

for(i=0; i<n; ++i){//如果父亲节点不同则变为最小路径并打印if(!Is_same(father,edge[i].x,edge[i].y)){v1 = edge[i].x;v2 = edge[i].y;printf("%c-->%c : %d\n",g->VerticesList[v1],g->VerticesList[v2],edge[i].cost);//改变父亲节点Mark_same(father,edge[i].x,edge[i].y);}}
}

5. Is_same方法解释

bool Is_same(int *father, int i, int j)
{
//寻找i的父节点while(father[i] != i){i = father[i];}//寻找j的父节点while(father[j] != j){j = father[j];}//判断i，j是否相等return i==j;
}

6. Mark_same方法解释

void Mark_same(int *father, int i, int j)
{
//寻找i的父节点while(father[i] != i){i = father[i];}//寻找j的父节点while(father[j] != j){j = father[j];}//将j的父节点转化为ifather[j] = i;
}