了解克鲁斯卡尔算法

article/2025/11/10 18:55:50

文章目录

- - - - Kruskal算法如何工作
      - Kruskal算法的示例
      - Kruskal算法伪代码
      - C示例
      - Kruskal算法 vs Prim算法
      - Kruskal算法的复杂度
      - Kruskal算法的应用
      - 参考文档

在本教程中，您将学习Kruskal算法如何工作。此外，您还将找到C语言的示例。
Kruskal算法是一种最小生成树算法，该算法将一个图作为输入并找到该图的边的子集，该子集

形成一棵包含每个顶点的树
在所有可以从图中形成的树中具有最小的权重之和

Kruskal算法如何工作

它属于一类称为贪心算法的算法，这种算法通过寻找局部最优，希望找到全局最优。
我们从权重最低的边开始，不断添加边，直到达到目的。
实现Kruskal算法的步骤如下：

将所有边按权重从低到高排序
取权重最小的边并将其添加到生成树中。如果添加边造成了循环，则不使用此边。
继续添加边，直到到达所有顶点。

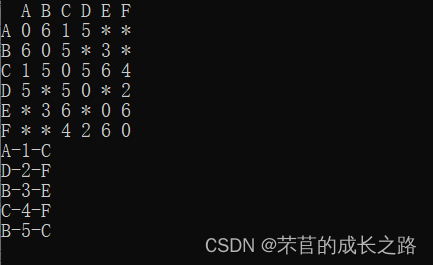
Kruskal算法的示例

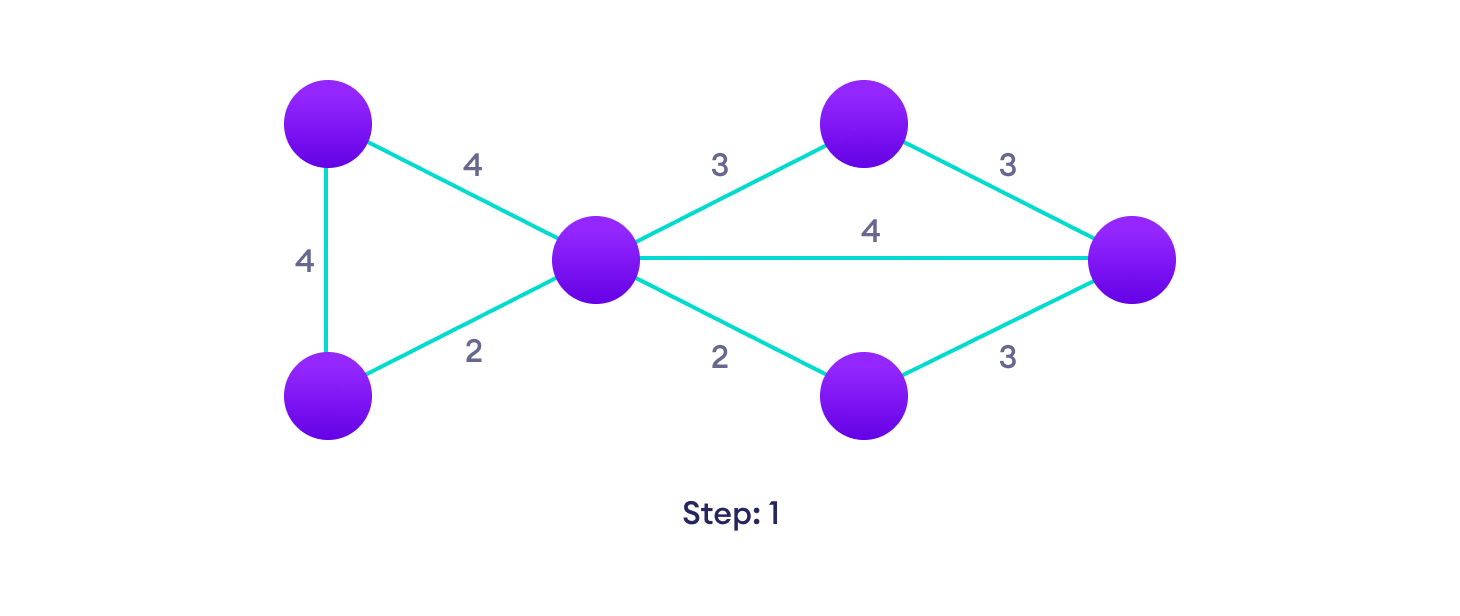
在这里插入图片描述
从加权图开始

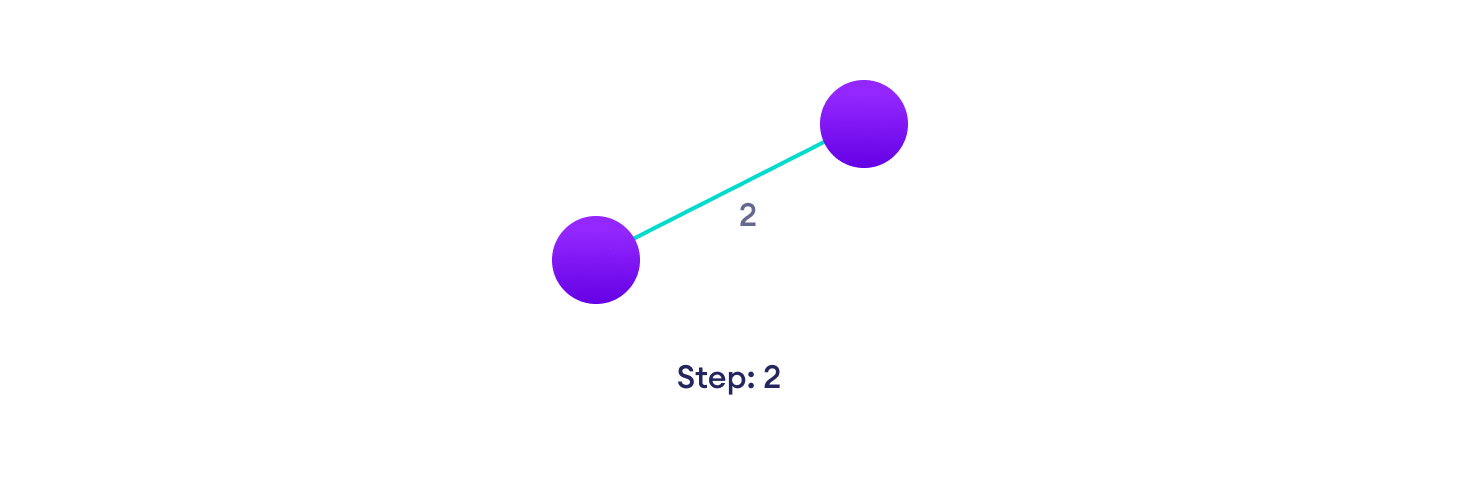
选择权重最小的边，如果有多个边，则任意选择一边

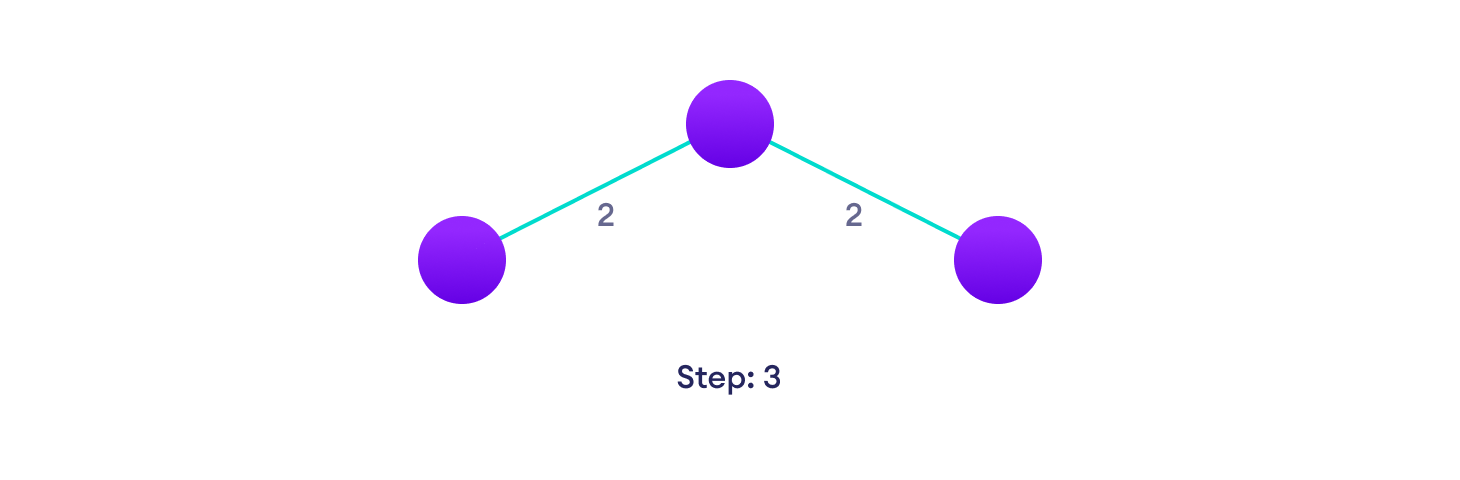
选择下一条最短边并添加

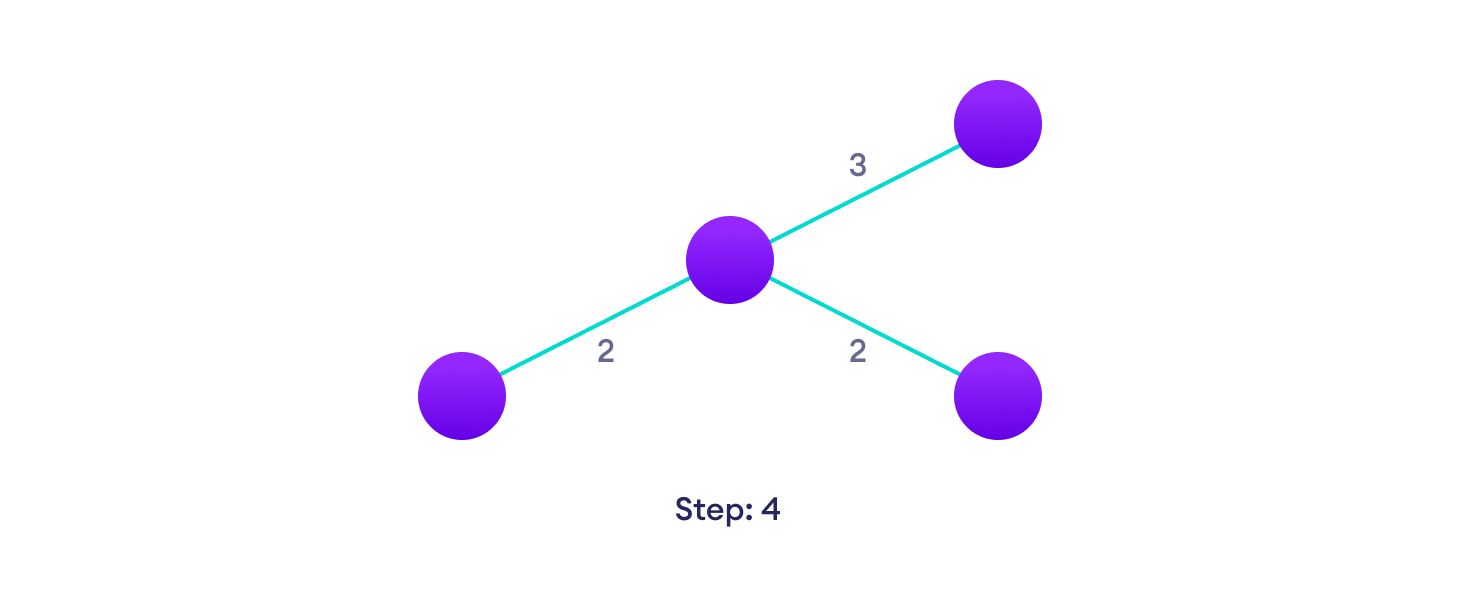
选择下一条不创建循环的最短边并将其添加

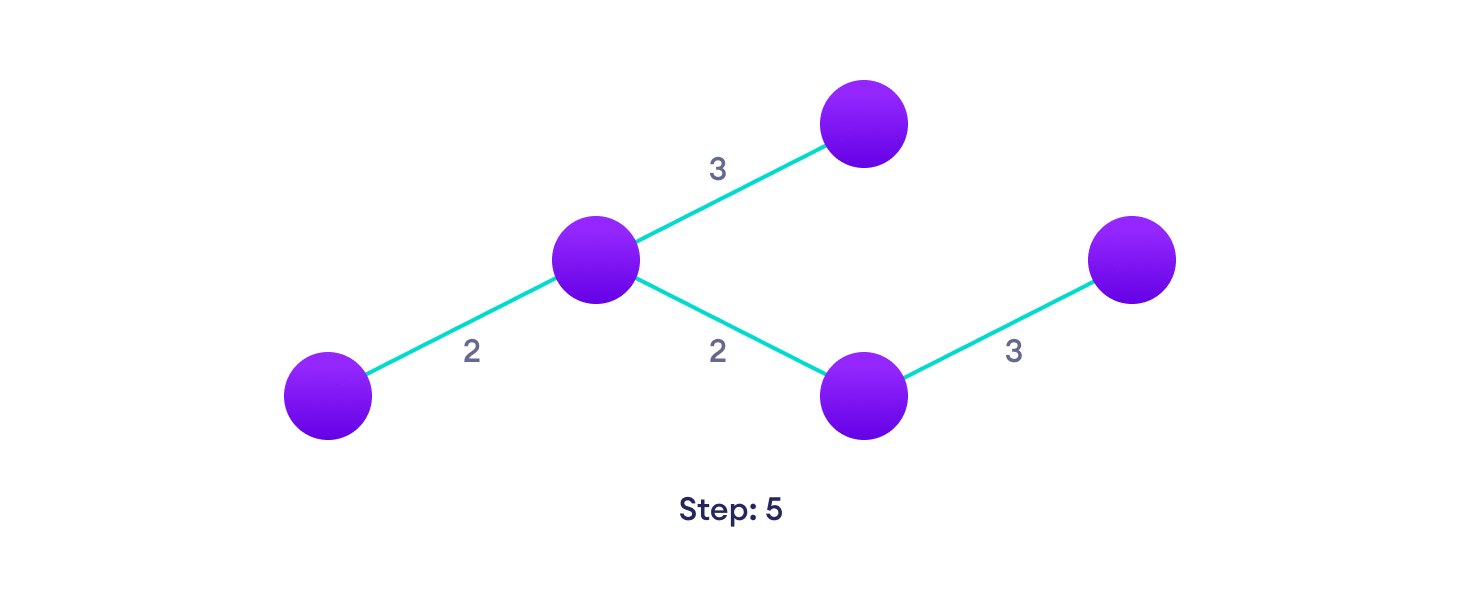
选择不创建循环的下一条最短边并添加它
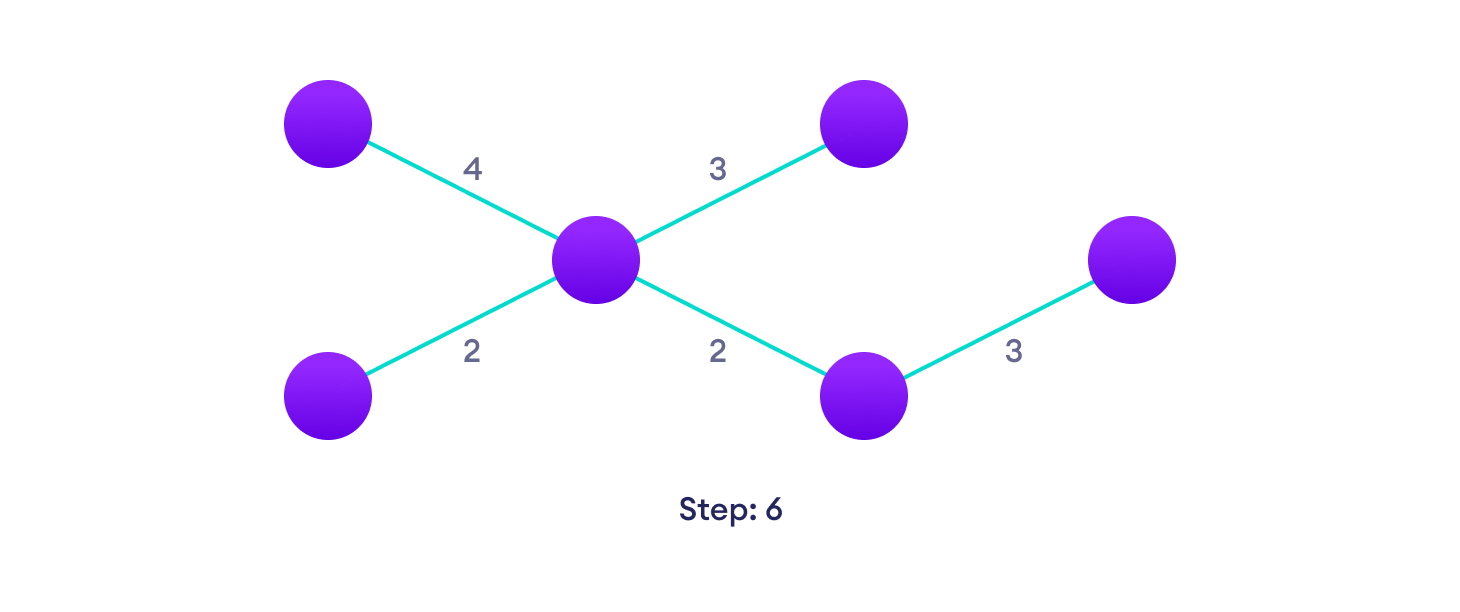
在这里插入图片描述
重复上述步骤，直到生成一棵生成树

Kruskal算法伪代码

任何最小生成树算法都围绕添加边是否创建循环来进行。
最常见的方法是一种称为联合查找（Union-Find）的算法。Union-Find算法将顶点划分为簇，并检查两个顶点是否属于同一簇，从而判断添加边是否创建循环。

KRUSKAL(G):
A = ∅
For each vertex v ∈ G.V:MAKE-SET(v)
For each edge (u, v) ∈ G.E ordered by increasing order by weight(u, v):if FIND-SET(u) ≠ FIND-SET(v):       A = A ∪ {(u, v)}UNION(u, v)
return A

C示例

// Kruskal's algorithm in C#include <stdio.h>#define MAX 30typedef struct edge {int u, v, w;
} edge;typedef struct edge_list {edge data[MAX];int n;
} edge_list;edge_list elist;int Graph[MAX][MAX], n;
edge_list spanlist;void kruskalAlgo();
int find(int belongs[], int vertexno);
void applyUnion(int belongs[], int c1, int c2);
void sort();
void print();// Applying Krushkal Algo
void kruskalAlgo() {int belongs[MAX], i, j, cno1, cno2;elist.n = 0;for (i = 1; i < n; i++)for (j = 0; j < i; j++) {if (Graph[i][j] != 0) {elist.data[elist.n].u = i;elist.data[elist.n].v = j;elist.data[elist.n].w = Graph[i][j];elist.n++;}}sort();for (i = 0; i < n; i++)belongs[i] = i;spanlist.n = 0;for (i = 0; i < elist.n; i++) {cno1 = find(belongs, elist.data[i].u);cno2 = find(belongs, elist.data[i].v);if (cno1 != cno2) {spanlist.data[spanlist.n] = elist.data[i];spanlist.n = spanlist.n + 1;applyUnion(belongs, cno1, cno2);}}
}int find(int belongs[], int vertexno) {return (belongs[vertexno]);
}void applyUnion(int belongs[], int c1, int c2) {int i;for (i = 0; i < n; i++)if (belongs[i] == c2)belongs[i] = c1;
}// Sorting algo
void sort() {int i, j;edge temp;for (i = 1; i < elist.n; i++)for (j = 0; j < elist.n - 1; j++)if (elist.data[j].w > elist.data[j + 1].w) {temp = elist.data[j];elist.data[j] = elist.data[j + 1];elist.data[j + 1] = temp;}
}// Printing the result
void print() {int i, cost = 0;for (i = 0; i < spanlist.n; i++) {printf("\n%d - %d : %d", spanlist.data[i].u, spanlist.data[i].v, spanlist.data[i].w);cost = cost + spanlist.data[i].w;}printf("\nSpanning tree cost: %d", cost);
}int main() {int i, j, total_cost;n = 6;Graph[0][0] = 0;Graph[0][1] = 4;Graph[0][2] = 4;Graph[0][3] = 0;Graph[0][4] = 0;Graph[0][5] = 0;Graph[0][6] = 0;Graph[1][0] = 4;Graph[1][1] = 0;Graph[1][2] = 2;Graph[1][3] = 0;Graph[1][4] = 0;Graph[1][5] = 0;Graph[1][6] = 0;Graph[2][0] = 4;Graph[2][1] = 2;Graph[2][2] = 0;Graph[2][3] = 3;Graph[2][4] = 4;Graph[2][5] = 0;Graph[2][6] = 0;Graph[3][0] = 0;Graph[3][1] = 0;Graph[3][2] = 3;Graph[3][3] = 0;Graph[3][4] = 3;Graph[3][5] = 0;Graph[3][6] = 0;Graph[4][0] = 0;Graph[4][1] = 0;Graph[4][2] = 4;Graph[4][3] = 3;Graph[4][4] = 0;Graph[4][5] = 0;Graph[4][6] = 0;Graph[5][0] = 0;Graph[5][1] = 0;Graph[5][2] = 2;Graph[5][3] = 0;Graph[5][4] = 3;Graph[5][5] = 0;Graph[5][6] = 0;kruskalAlgo();print();
}