数据结构——克鲁斯卡尔（Kruskal）算法

克鲁斯卡尔算法是求连通网的最小生成树的另一种方法。与普里姆算法不同，它的时间复杂度为O（eloge）（e为边数），适合于求边稀疏的网的最小生成树。克鲁斯卡尔算法从另一途径求网的最小生成树。其基本思想是：假设连通网G，令最小生成树的初始状态为只有n个顶点而无边的非连通图T，概述图中每个顶点自成一个连通分量。在E中选择代价最小的边，若该边依附的顶点分别在T中不同的连通分量上，则将此边加入到T中；否则，舍去此边而选择下一条代价最小的边。说白了，优先先选出全体边里最短的那几条，然后如果各分量还没连起来，就继续选择剩余没被选择的边里最短的，直到全部节点都连接在一起。
以下是数据结构中关于克鲁斯卡尔算法的操作（编程风格参考严蔚敏版数据结构）。

宏定义及头文件

#include<iostream>
#include<stdio.h>
using namespace std; 
typedef char VerTexType; 
typedef int ArcType; 
#define MaxInt 32767 
#define MVNum 100
#define ArcNum 100
#define OK 1
#define ERROR -1
int Vexset[MVNum];//辅助数组表示连通分量 
typedef int status;

图和边集合的声明

typedef struct{VerTexType vexs[MVNum] {'A','B','C','D','E','F'};ArcType arcs[MVNum][MVNum];int vexnum = 6,arcnum = 10;
}AMGraph; typedef struct{VerTexType Head;//起点 VerTexType Tail;//终点ArcType lowcast; 
}Edge[ArcNum];

说明：为了测试方便就提前写好了图里节点和边的数据。
edge是记录原始的图里全部边数据（包括起点、终点以及权值）

Kruskal辅助数组Vexset

int Vexset[MVNum];//辅助数组表示连通分量

这里一定要理解好Vexset数组的作用和意义。如果这个理解不好，就像prim算法不理解close数组一样，核心算法就理解不了了。
Vexset是以下标i表示节点，以数组的值表示该点的连通量。
如：Vexset[1] = 0，Vexset[0] = 0.表示B节点和A节点是同一个连通量（B的下标为1，A的下标为0）。

Kruskal核心算法：

void Kruskal(AMGraph &G){Edge edge;InitailEdge(G,edge);sort(G,edge);
//	ShowEdge(G,edge);for(int i=0;i<G.vexnum;i++){Vexset[i] = i;//每个节点自成一个分量 }int headi,taili;//边起点的下标、边终点的下标 int headt,tailt;//操作连通分量时的中间量 for(int i=0;i<G.arcnum;i++){headi = LocateVex(G,edge[i].Head); taili = LocateVex(G,edge[i].Tail); headt = Vexset[headi];tailt = Vexset[taili];if(headt!=tailt){//如果两个点不是同一个连通分量cout<<edge[i].Head<<"-"<<edge[i].lowcast<<"-"<<edge[i].Tail<<endl;for(int j=0;j<G.vexnum;j++){if(Vexset[j]==headt){//合并选出来的两个节点，使其处于同一个连通分量Vexset[j] = tailt;}}}} 
}

代码执行过程：
1、初始化边集合：把图里全部边加入边集合（集合里边的数量就是图里边的数量）。
2、初始化辅助数组Vexset：每个节点自己属于一个连通量（毕竟刚开始谁都没连接谁是吧）。
3、将边集合按照边权值从小到大排序，让循环操作从小边到大边的顺序进行选择。
4、循环获取每一条边的起点和终点。
5、如果起点和终点不是同一个连通分量，就把两个点连起来（合并连通量）。
6、全部点同属一个连通分量，循环结束。

举例子手推算法过程：

此次选的例子还是书上的例子：
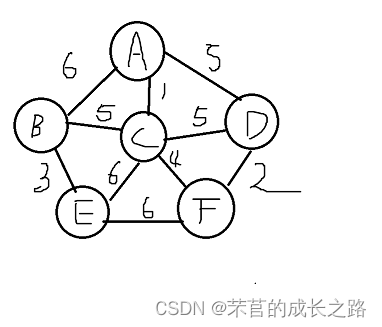
在这里插入图片描述
老样子先弄出邻接矩阵：

第一步：初始化边集合

第二步：初始化Vexset集合（每个节点分别代表一个连通分量），ABCDEF下标分别对应012345，所以ABCDEF的连通量分别是012345。

第三步（第二第三步可互换）：边集合按边权值从小到大排序

第四步：大循环获取每一条边，看其两个端点是否是同一个连通量（因为边集合排过序了，每一次选择的肯定是未被选择的边集合里最短的边）。下面是大循环的执行过程：
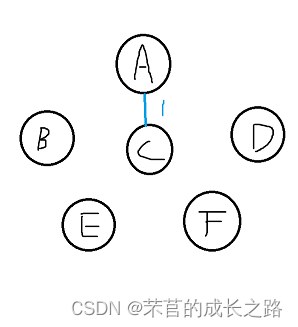
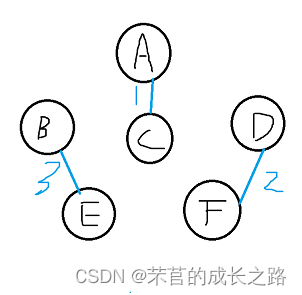
1)、选出AC（权值为1），此时A和C的连通分量不一样（A是0，C是2），将AC的连通量合并（此处的操作是将A的连通量修改成和C一致），此时A和C连通量都是2；小循环未发现和C变化前连通量相同（0）的其它节点（这一步的目的是找出原来的起点，一起并入边集合中），故无实际操作；
此时的Vexset为｛2，1，2，3，4，5｝。

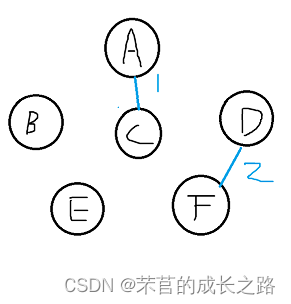
2)、选出DF（权值为2），此时D和F的连通分量不一样（D是3，F是5），将DF的连通量合并，此时D和F连通量都是5；小循环未发现和D变化前连通量相同（3）的其它节点，故无实际操作；
此时的Vexset为｛2，1，2，5，4，5｝。

3)、选出BE（权值为3），此时BE连通分量不一样（B是1，E是4），将BE连通量合并，此时B和E连通量都是4。小循环未发现和B变化前连通量相同（1）的其它节点，故无实际操作；
此时的Vexset为｛2，4，2，5，4，5｝。

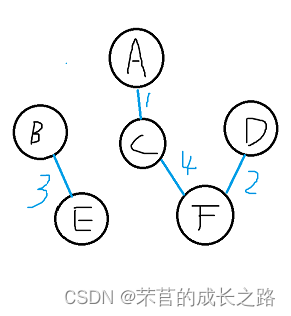
4)、选出CF（权值为4），此时CF的连通量不一样（C是2，F是5），将CF连通量合并，此时C和F连通量都是5。小循环发现和C变化前连通量相同（2）的其它节点A，故将A的连通量也修改成F的连通量（5）；
此时的Vexset为｛5，4，5，5，4，5｝。

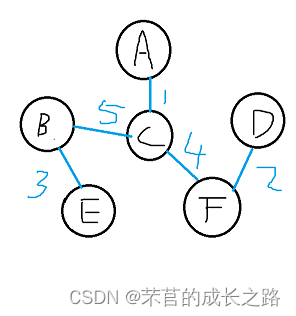
5)、选出AD（权值为5），此时AD连通量一样（A是5，D是5），无操作。
6)、选出BC，此时BC连通分量不一样（B是4，C是5），将BC连通量合并，此时B和C连通量都是5。小循环发现和B变化前连通量相同（4）的其它节点E，故将E的连通量也修改成C的连通量（5）；
此时的Vexset为｛5，5，5，5，5，5｝。

往后循环，每个点的连通分量都一致，故均无实际操作，直至循环结束。

运行结果

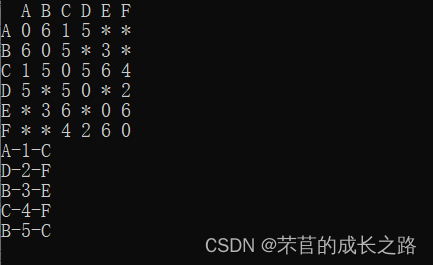
在这里插入图片描述

源代码

#include<iostream>
#include<stdio.h>
using namespace std; 
typedef char VerTexType; 
typedef int ArcType; 
#define MaxInt 32767 
#define MVNum 100
#define ArcNum 100
#define OK 1
#define ERROR -1
int Vexset[MVNum];//辅助数组表示连通分量 
typedef int status;
typedef struct{VerTexType vexs[MVNum] {'A','B','C','D','E','F'};ArcType arcs[MVNum][MVNum];int vexnum = 6,arcnum = 10;
}AMGraph; typedef struct{VerTexType Head;//起点 VerTexType Tail;//终点ArcType lowcast; 
}Edge[ArcNum];status CreateUDN(AMGraph &G){//创建无向图 	for(int i=0;i<G.vexnum;i++){for(int j=0;j<G.vexnum;j++){if(i==j){G.arcs[i][j] = 0;}elseG.arcs[i][j] = MaxInt;//初始状态全部节点之间相互不可达}}G.arcs[0][1]=6;G.arcs[0][2]=1;G.arcs[0][3]=5;G.arcs[1][2]=5;G.arcs[1][4]=3;G.arcs[2][3]=5;G.arcs[2][4]=6;G.arcs[2][5]=4;G.arcs[3][5]=2;G.arcs[4][5]=6;for(int i=0;i<G.vexnum;i++){for(int j=i+1;j<G.vexnum;j++){if(G.arcs[i][j]!=MaxInt){G.arcs[j][i] = G.arcs[i][j];} }}//矩阵对称 return OK; 
}void ShowGraph(AMGraph G){cout<<" ";for(int i=0;i<G.vexnum;i++){cout<<" "<<G.vexs[i];}cout<<endl;for(int i=0;i<G.vexnum;i++){cout<<G.vexs[i]<<" ";for(int j=0;j<G.vexnum;j++){if(G.arcs[i][j]==MaxInt){cout<<"* ";}else{cout<<G.arcs[i][j]<<" ";}}cout<<endl;}
}int LocateVex(AMGraph G, VerTexType v){int i;for(i=0;i<G.vexnum;i++){if(G.vexs[i]==v){return i;}} return ERROR;
}VerTexType Transform(AMGraph G, int vn){return G.vexs[vn]; 
}void InitailEdge(AMGraph G,Edge &edge){//初始化边表 int arcnum = 0;for(int i=0;i<G.vexnum;i++){//纵列为起点 for(int j=i+1;j<G.vexnum;j++){//横行为终点 if(G.arcs[i][j]!=MaxInt&&G.arcs[i][j]!=0){edge[arcnum].Head = Transform(G,i);edge[arcnum].Tail = Transform(G,j);edge[arcnum].lowcast = G.arcs[i][j];arcnum++;}}} 
}void sort(AMGraph G,Edge &edge){VerTexType tv;ArcType tl;for(int i=0;i<G.arcnum;i++){for(int j=0;j<G.arcnum-i-1;j++){if(edge[j].lowcast>edge[j+1].lowcast){//直接写对象互换报错，忘记咋互换对象了，这样写有点麻烦，先将就着用吧 ，这个操作不是重点 tv = edge[j].Head;edge[j].Head = edge[j+1].Head;edge[j+1].Head = tv;tv = edge[j].Tail;edge[j].Tail = edge[j+1].Tail;edge[j+1].Tail = tv;tl = edge[j].lowcast;edge[j].lowcast = edge[j+1].lowcast;edge[j+1].lowcast = tl;}}}
}void ShowEdge(AMGraph G,Edge edge){for(int i=0;i<G.arcnum;i++){cout<<edge[i].Head<<"-"<<edge[i].lowcast<<"-"<<edge[i].Tail<<endl;}
}void ShowVexset(AMGraph G){for(int i=0;i<G.vexnum;i++){cout<<Vexset[i]<<" ";} cout<<endl;
}void Kruskal(AMGraph &G){Edge edge;InitailEdge(G,edge); 
//	ShowEdge(G,edge);sort(G,edge);
//	ShowEdge(G,edge);for(int i=0;i<G.vexnum;i++){Vexset[i] = i;//每个节点自成一个分量 }int headi,taili;//边起点的下标、边终点的下标 int headt,tailt;//操作连通分量时的中间量 for(int i=0;i<G.arcnum;i++){headi = LocateVex(G,edge[i].Head); //起点下标 taili = LocateVex(G,edge[i].Tail); //终点下标 headt = Vexset[headi];//获取起点的连通分量 tailt = Vexset[taili];//获取终点的连通分量 if(headt!=tailt){//如果两个点不是同一个连通分量cout<<edge[i].Head<<"-"<<edge[i].lowcast<<"-"<<edge[i].Tail<<endl;for(int j=0;j<G.vexnum;j++){if(Vexset[j]==headt){//更新Vexset数组，把改起点的连通分量改成和终点连通分量一致（其实就是合并连通分量） Vexset[j] = tailt;
//					ShowVexset(G);}}}} 	
}int main(){AMGraph G;CreateUDN(G);ShowGraph(G);Kruskal(G); return 0;
}