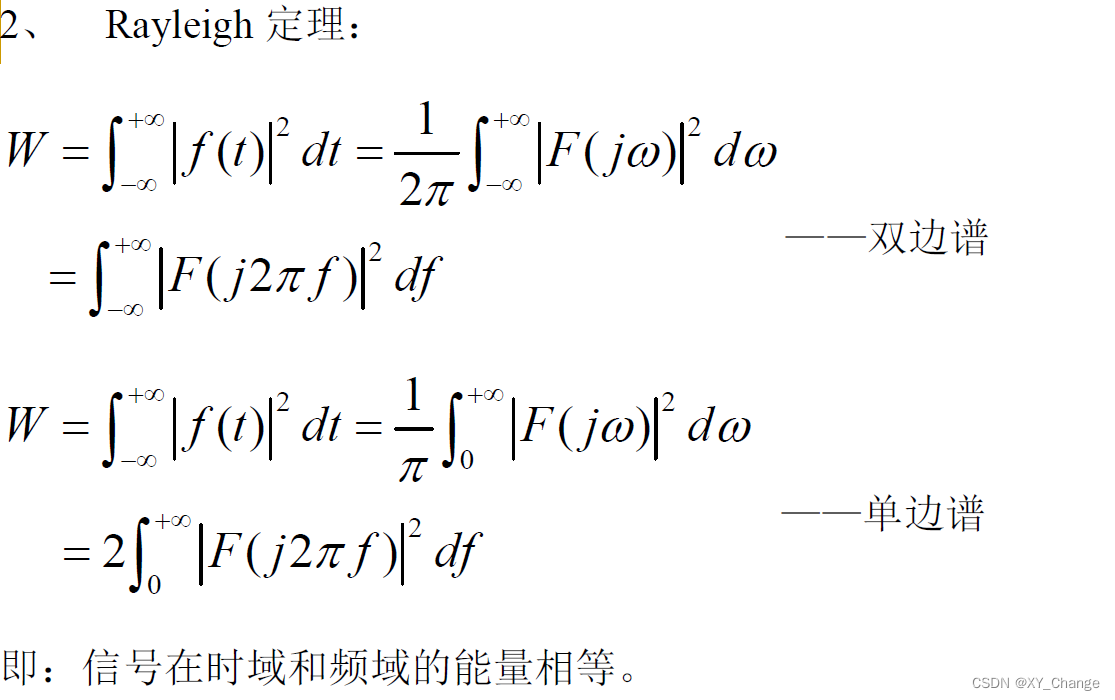1、线性特性

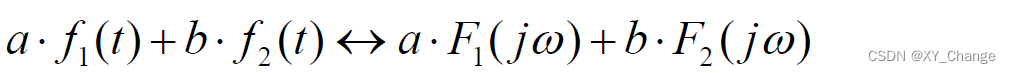
2、延时特性

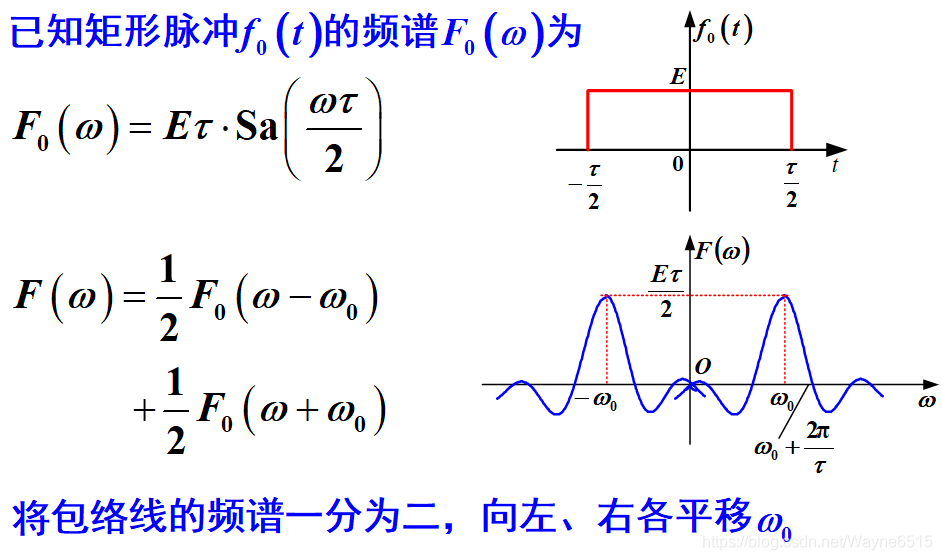
3、频移特性

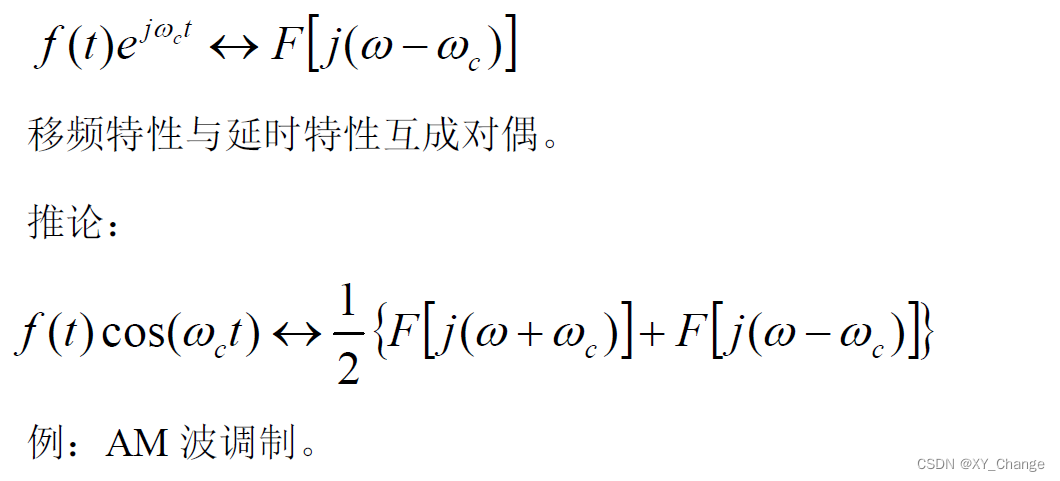
4、尺度变换

5、奇偶虚实性

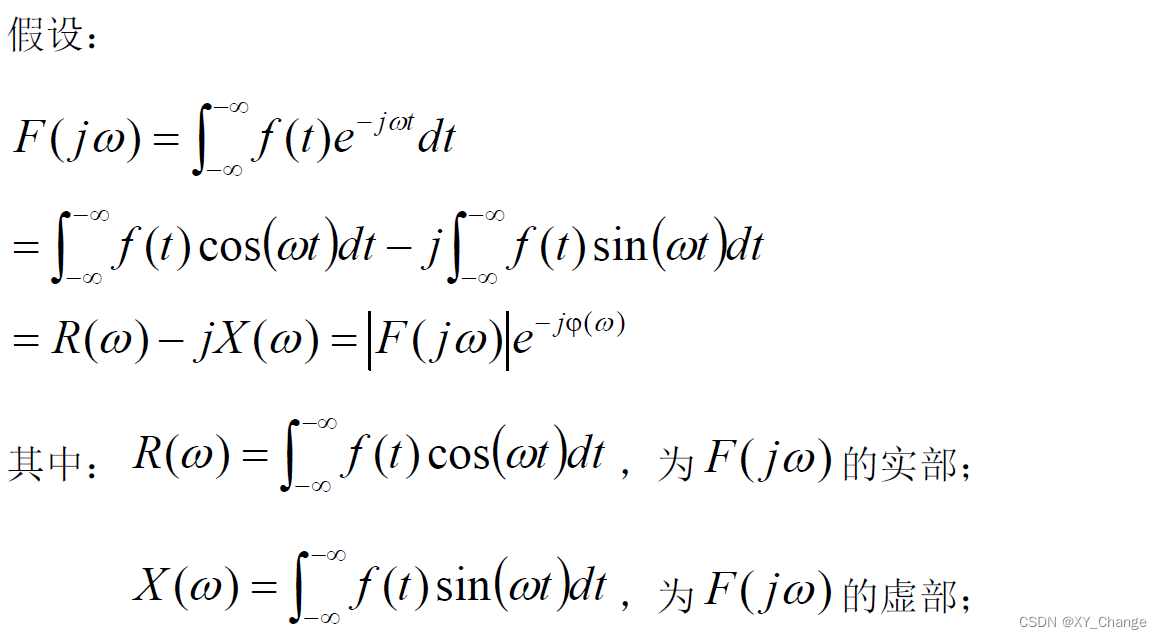
6、对称特性

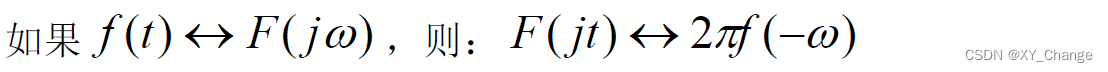
当f函数是偶函数，f(-w)=f(w).

7、微分特性

8、积分特性

在工程应用中，多次做积分比较少，多次做微分很多。

9、频域微积分特性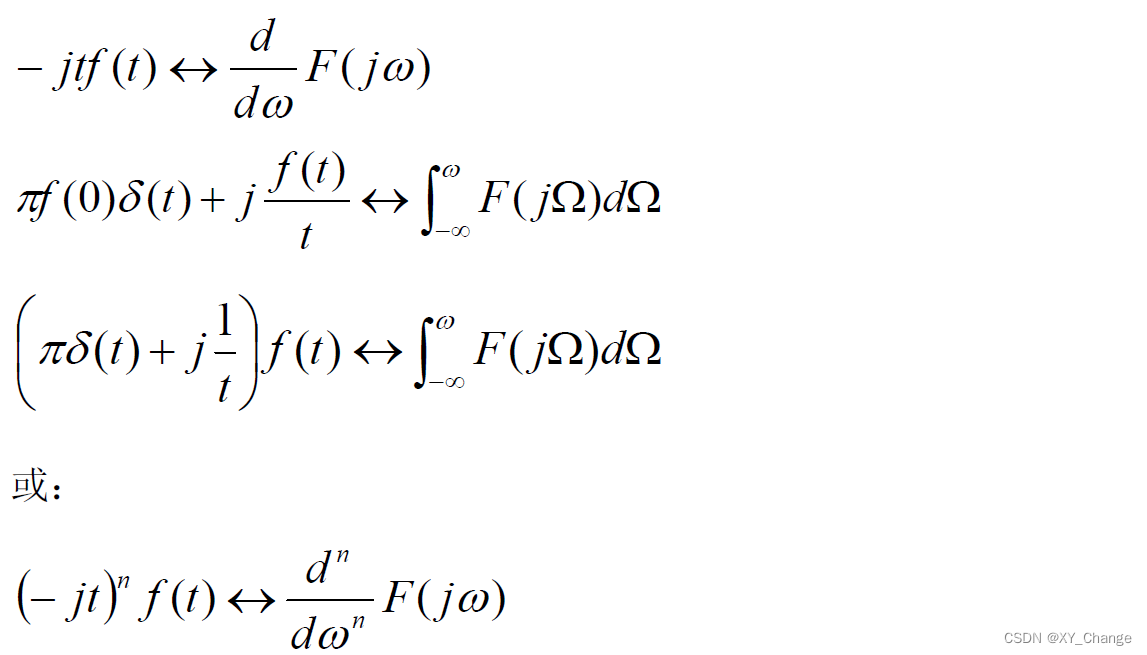

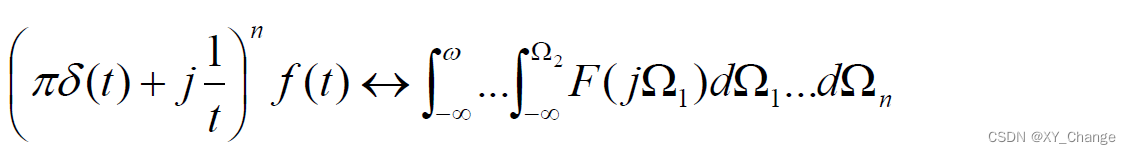
工程中，一般实数函数乘j没有实际意义，这个用得少。不过在可以进行俩边同时乘以j.

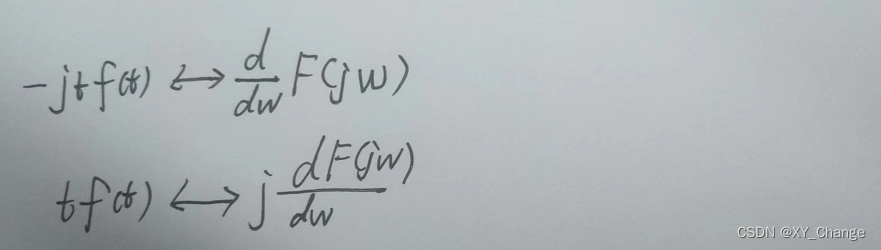
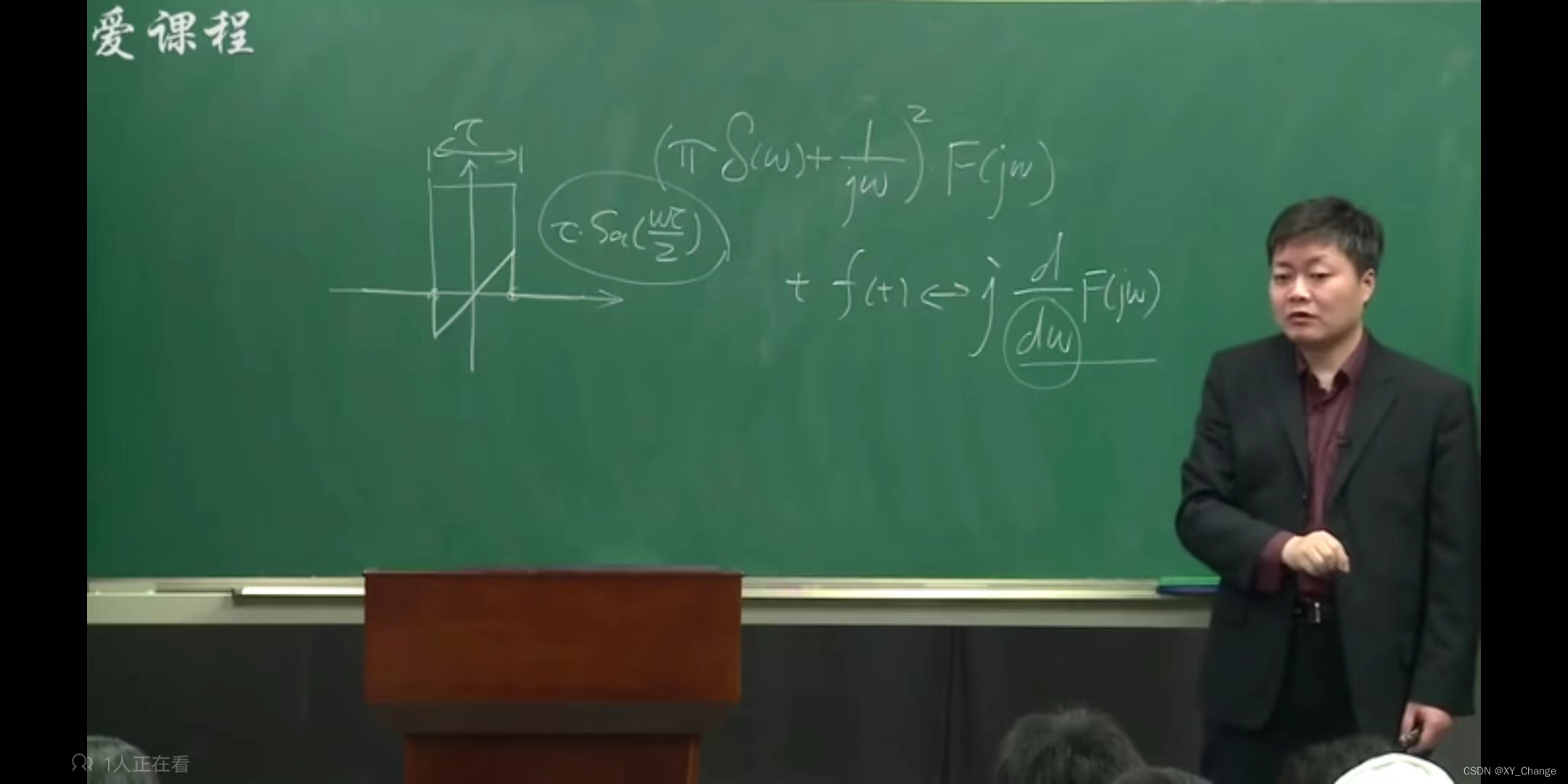
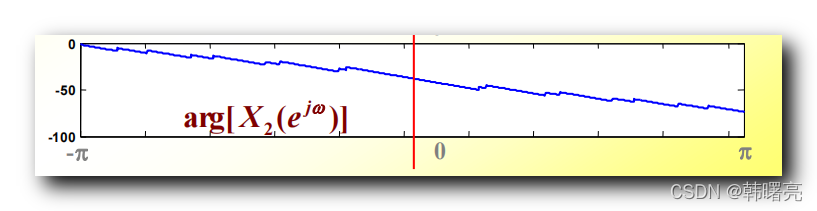
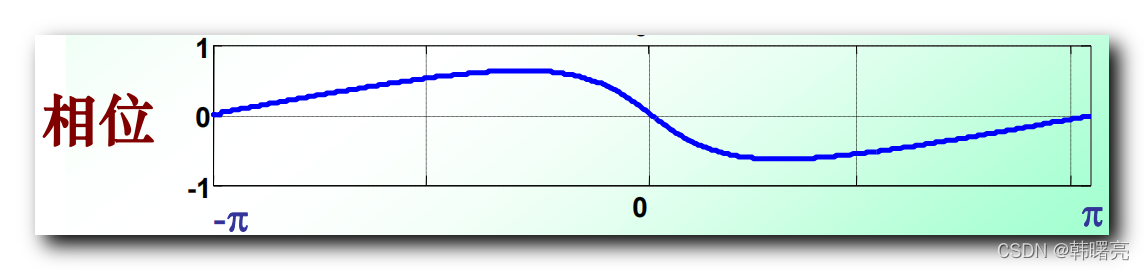
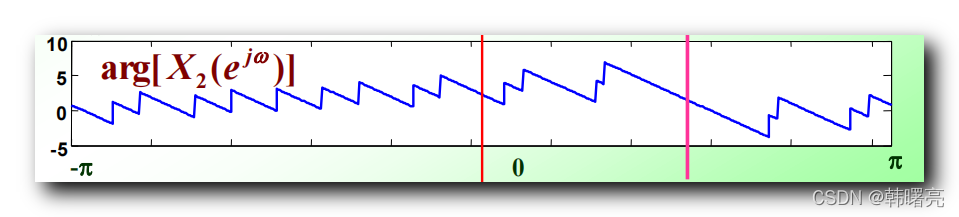
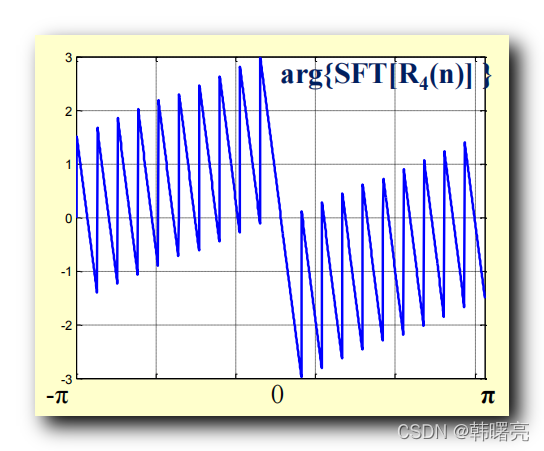
注意下图，红色信号和白色信号不一样，若是用图中求法好像一样了，是典型的错误，错误在于w=0时没有排除在外，微分与积分不是完全可逆的。

那么白色信号的正确傅里叶变换在w=0时考虑进来是

那么红色信号的傅里叶变换，只要把时域里红色信号距离白色信号的常数C的傅里叶变换加上白色信号的傅里叶变换就是红色信号的傅里叶变换。

10、卷积定理

第二章里，任何一个系统的零状态响应，可以等于两个信号的卷积，一个是输入的激励信号，还有一个是系统的冲激响应。如果两个信号相卷积，那么频域里是什么样表现形式？

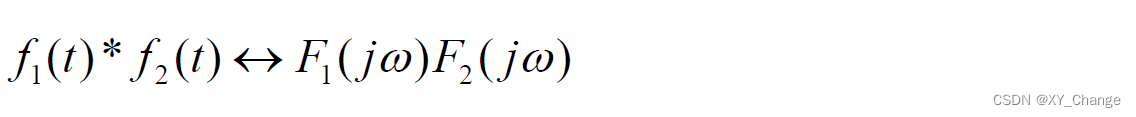
根据堆成特性，那么时域相乘积，频域肯定相卷积

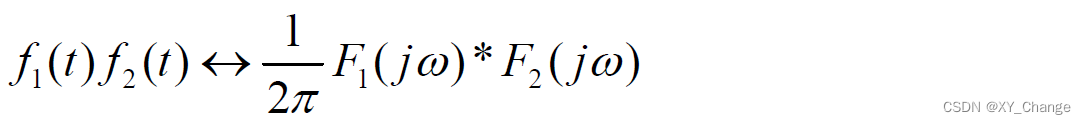
灵活应用上面十大性质，就可以比较方便的来求信号的傅里叶变换
比如，求解三角波信号的傅里叶变换，可以是俩简便方法，其中求卷积最简单

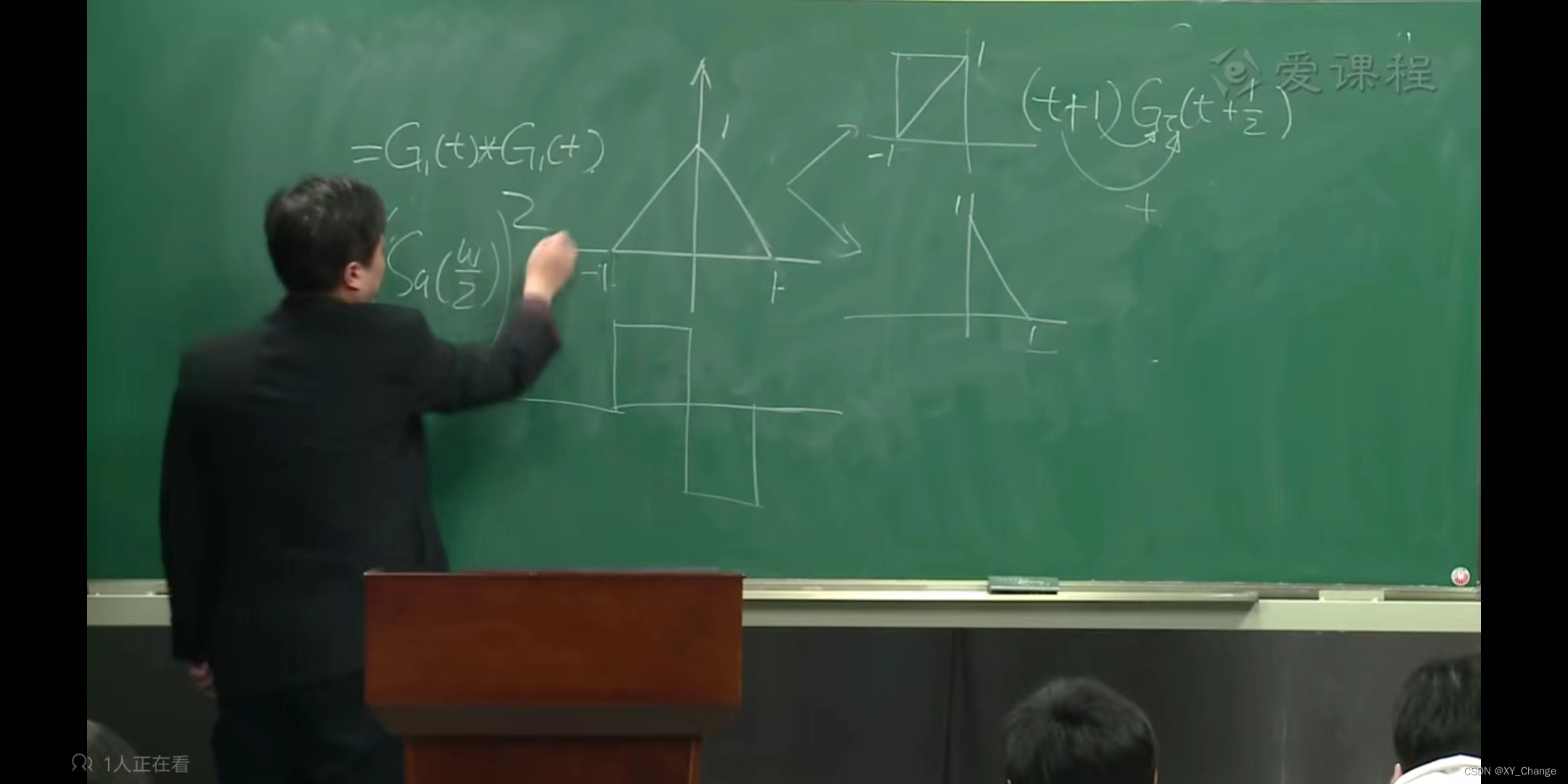
下面再举一例，此例子告诉我们要慎用性质。对于t乘以阶跃函数的傅里叶变换，你用三条性质就出来了三个答案，那么现在问你，着三个答案相等吗？
孟桥认为这三个结论都是不对的。我们所有的证明过程技巧都是在调换次序，比如先做A积分再做B积分，但是我们也可以先做B积分，再做A积分，可以先做求和再做积分，也可以先做积分再做求和，可以做任意的调换，但是调换成立的条件是什么？条件是调换前后的结果都存在且有限的话，两者都相等，否则就不行。
所以对于t乘以阶跃函数的傅里叶变换不满足狄利克雷条件，（直流和阶跃函数不满足条件，但是其结果是在冲激函数的帮助下求出来的，而这种t乘以阶跃函数变化要大，所以孟认为其实这样的东西傅里叶变换不存在，即使拿冲激函数也写不出来，所以基于冲激函数算出来的，可能三个之间没有一个是正确的）。另外，在实际工程当中，没有这样的信号，哪里去找一个无穷远的时候趋向于无穷大的电压或电流信号吗？所以这样的函数信号我们是不关心的。

其实有人说不只十大性质，有第十一大性质，因为涉及太大，所以特意单独领出来，即

能量频谱和功率频谱

对于上面的的公式，当然，其实大多数都是实数信号，如果是复数，那么前边就要成f(t)绝对值的平方

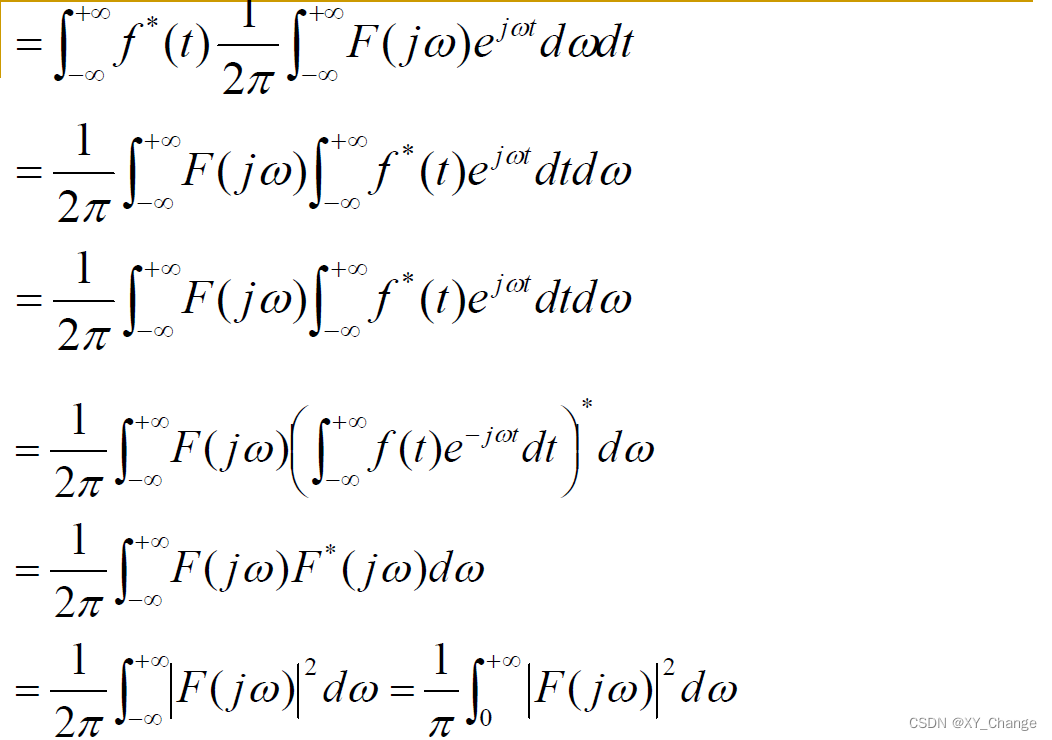
积分变换的能量不变性：这个性质意义是工程上，哪个好算用哪一个，比如现在让你算Sa(t)信号的能量，但是可以根据在频域里算门信号的面积来等换。