文章目录
- 一、序列傅里叶变换共轭对称性质示例
- 1、序列傅里叶变换共轭对称性质
- 1、序列实部傅里叶变换
- 2、序列虚部傅里叶变换
- 3、共轭对称序列傅里叶变换
- 4、共轭反对称序列傅里叶变换
- 2、求 a^n u(n) 的傅里叶变换
- 3、序列分析
一、序列傅里叶变换共轭对称性质示例
x ( n ) = a n u ( n ) x(n) = a^n u(n) x(n)=anu(n) , 且 ∣ a ∣ < 1 |a|<1 ∣a∣<1
1、序列傅里叶变换共轭对称性质
1、序列实部傅里叶变换
x ( n ) x(n) x(n) 序列的 实部 x R ( n ) x_R(n) xR(n) 的 傅里叶变换 , 就是 x ( n ) x(n) x(n) 的 傅里叶变换 X ( e j ω ) X(e^{j \omega}) X(ejω) 的 共轭对称序列 X e ( e j ω ) X_e(e^{j \omega}) Xe(ejω);
x R ( n ) x_R(n) xR(n) 的 傅里叶变换 X e ( e j ω ) X_e(e^{j \omega}) Xe(ejω) 具备 共轭对称性 ;
x R ( n ) ⟷ S F T X e ( e j ω ) x_R(n) \overset{SFT} \longleftrightarrow X_e(e^{j \omega}) xR(n)⟷SFTXe(ejω)
2、序列虚部傅里叶变换
x ( n ) x(n) x(n) 序列的 虚部 x I ( n ) x_I(n) xI(n) 的 傅里叶变换 , 就是 x ( n ) x(n) x(n) 的 傅里叶变换 X ( e j ω ) X(e^{j \omega}) X(ejω) 的 共轭反对称序列 X o ( e j ω ) X_o(e^{j \omega}) Xo(ejω);
j x I ( n ) jx_I(n) jxI(n) 的 傅里叶变换 X o ( e j ω ) X_o(e^{j \omega}) Xo(ejω) 具备 共轭反对称性 :
j x I ( n ) ⟷ S F T X o ( e j ω ) jx_I(n) \overset{SFT} \longleftrightarrow X_o(e^{j \omega}) jxI(n)⟷SFTXo(ejω)
3、共轭对称序列傅里叶变换
x ( n ) x(n) x(n) 的 共轭对称序列 x e ( n ) x_e(n) xe(n) 的 傅里叶变换 , 一定是一个 实序列 X R ( e j ω ) X_R(e^{j \omega}) XR(ejω)
x e ( n ) ⟷ S F T X R ( e j ω ) x_e(n) \overset{SFT} \longleftrightarrow X_R(e^{j \omega}) xe(n)⟷SFTXR(ejω)
4、共轭反对称序列傅里叶变换
x ( n ) x(n) x(n) 的 共轭反对称序列 x o ( n ) x_o(n) xo(n) 的 傅里叶变换 , 一定是一个 纯虚序列 X R ( e j ω ) X_R(e^{j \omega}) XR(ejω)
x o ( n ) ⟷ S F T j X I ( e j ω ) x_o(n) \overset{SFT} \longleftrightarrow jX_I(e^{j \omega}) xo(n)⟷SFTjXI(ejω)
2、求 a^n u(n) 的傅里叶变换
根据 傅里叶变换公式 计算 x ( n ) x(n) x(n) 的傅里叶变换 , 公式如下 :
X ( e j ω ) = ∑ n = − ∞ + ∞ x ( n ) e − j ω n X(e^{j\omega}) = \sum_{n=-\infty}^{+\infty} x(n) e^{-j \omega n} X(ejω)=n=−∞∑+∞x(n)e−jωn
将
a n u ( n ) a^nu(n) anu(n)
序列 , 直接带入到
X ( e j ω ) = ∑ n = − ∞ + ∞ x ( n ) e − j ω n X(e^{j\omega}) = \sum_{n=-\infty}^{+\infty} x(n) e^{-j \omega n} X(ejω)=n=−∞∑+∞x(n)e−jωn
傅里叶变换公式中 , 可得到 :
X ( e j ω ) = ∑ n = 0 + ∞ a n e − j ω n X(e^{j\omega}) = \sum_{n=0}^{+\infty} a^n e^{-j \omega n} X(ejω)=n=0∑+∞ane−jωn
根据 " 等比级数求和 " 公式 , 可以得到
X ( e j ω ) = 1 1 − a e − j ω X(e^{j\omega}) = \cfrac{1}{1-ae^{-j \omega}} X(ejω)=1−ae−jω1
3、序列分析
该信号 x ( n ) x(n) x(n) 是实信号 , 该信号既不是偶对称的 , 也不是奇对称的 ;
-
只有序列是偶对称时 , 才有 x e ( n ) ⟷ S F T X R ( e j ω ) x_e(n) \overset{SFT} \longleftrightarrow X_R(e^{j \omega}) xe(n)⟷SFTXR(ejω) 性质 ,
-
只有序列是奇对称时 , 才有 x o ( n ) ⟷ S F T j X I ( e j ω ) x_o(n) \overset{SFT} \longleftrightarrow jX_I(e^{j \omega}) xo(n)⟷SFTjXI(ejω) 性质 ;
因此 , 这里 x ( n ) x(n) x(n) 的傅里叶变换 , 既不是实数 , 也不是虚数 , 那么就一定是复数 ;
分析 x ( n ) x(n) x(n) 的傅里叶变换 复数序列的 实部 和 虚部 :
由于 x ( n ) = a n u ( n ) x(n) = a^n u(n) x(n)=anu(n) 序列是实数 ,
其 傅里叶变换
S F T [ x ( n ) ] = X ( e j ω ) = 1 1 − a e − j ω SFT[x(n)] =X(e^{j\omega}) = \cfrac{1}{1-ae^{-j \omega}} SFT[x(n)]=X(ejω)=1−ae−jω1
一定是共轭对称的 ;
分解 S F T [ x ( n ) ] SFT[x(n)] SFT[x(n)] 的实部和虚部 :
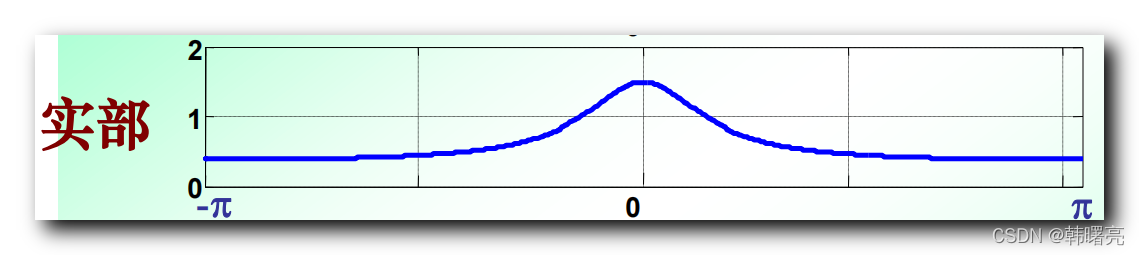
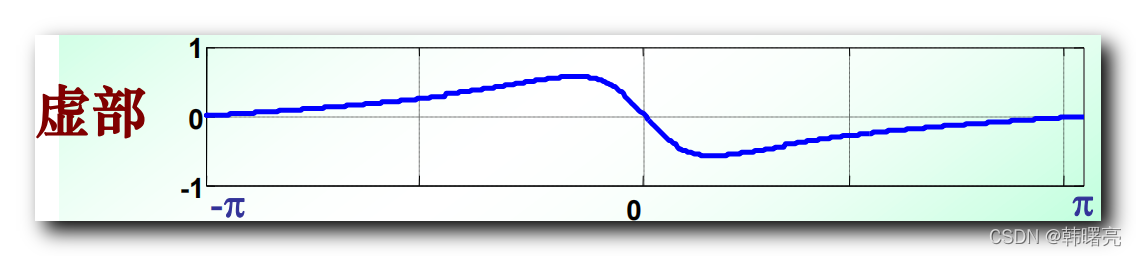
X ( e j ω ) = 1 − a cos ω 1 + a 2 − 2 a cos ω − j a sin ω 1 + a 2 − 2 a cos ω X(e^{j\omega}) = \cfrac{1 - a\cos \omega}{1 + a^2 - 2a\cos \omega } - j\cfrac{a\sin \omega}{1 + a^2 - 2a\cos \omega } X(ejω)=1+a2−2acosω1−acosω−j1+a2−2acosωasinω
共轭对称 的 傅里叶变换 , 实部是 偶对称的 , 虚部是 奇对称 的 ;
傅里叶变换的 模 , 即 傅里叶变换 取绝对值 ∣ X ( e j ω ) ∣ |X(e^{j\omega})| ∣X(ejω)∣ , 是偶对称的 ;
∣ X ( e j ω ) ∣ = 1 ( 1 + a 2 − 2 a cos ω ) 1 2 |X(e^{j\omega})| = \cfrac{1}{ ( 1 + a^2 - 2a\cos \omega )^{\frac{1}{2}} } ∣X(ejω)∣=(1+a2−2acosω)211
根据如下定理 : x ( n ) x(n) x(n) 的 共轭对称序列 x e ( n ) x_e(n) xe(n) 的 傅里叶变换 , 一定是一个 实序列 X R ( e j ω ) X_R(e^{j \omega}) XR(ejω)
x e ( n ) ⟷ S F T X R ( e j ω ) x_e(n) \overset{SFT} \longleftrightarrow X_R(e^{j \omega}) xe(n)⟷SFTXR(ejω)
可得 : 傅里叶变换的 实部 1 − a cos ω 1 + a 2 − 2 a cos ω \cfrac{1 - a\cos \omega}{1 + a^2 - 2a\cos \omega } 1+a2−2acosω1−acosω 的 傅里叶反变换 , 对应的是 x ( n ) x(n) x(n) 的共轭对称分量 ;
傅里叶变换的 虚部 − j a sin ω 1 + a 2 − 2 a cos ω - j\cfrac{a\sin \omega}{1 + a^2 - 2a\cos \omega } −j1+a2−2acosωasinω 的 傅里叶反变换 , 对应的是 x ( n ) x(n) x(n) 的共轭反对称分量 ;
在 【数字信号处理】傅里叶变换性质 ( 序列对称分解定理示例 | 共轭对称序列与原序列之间的关系 | 共轭反对称序列与原序列之间的关系 ) 博客中 , 推导了 共轭对称序列 与原序列的关系 , 这里当做一个先决的条件 , 之后需要使用 ;
实因果序列的对称序列与原序列关系 : 先将结果放在这里 , 之后需要使用 ;
h e ( n ) h_e(n) he(n) 与 h ( n ) h(n) h(n) 关系 :
h e ( n ) = { h ( 0 ) n = 0 h ( n ) 2 n > 0 h ( − n ) 2 n < 0 h_e(n) =\begin{cases} h(0) & n = 0 \\\\ \cfrac{h(n)}{2} & n > 0 \\\\ \cfrac{h(-n)}{2} & n < 0 \end{cases} he(n)=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧h(0)2h(n)2h(−n)n=0n>0n<0
h o ( n ) h_o(n) ho(n) 与 h ( n ) h(n) h(n) 关系 :
h o ( n ) = { 0 n = 0 h ( n ) 2 n > 0 − h ( − n ) 2 n < 0 h_o(n) =\begin{cases} 0 & n = 0 \\\\ \cfrac{h(n)}{2} & n > 0 \\\\ \cfrac{-h(-n)}{2} & n < 0 \end{cases} ho(n)=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧02h(n)2−h(−n)n=0n>0n<0
下面继续分析上述序列 :
下面的序列 x e ( n ) x_e(n) xe(n) 为实偶 ,
x e ( n ) = { 1 n = 0 a n 2 n > 0 a − n 2 n < 0 x_e(n) =\begin{cases} 1 & n = 0 \\\\ \cfrac{a^n}{2} & n > 0 \\\\ \cfrac{a^{-n}}{2} & n < 0 \end{cases} xe(n)=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧12an2a−nn=0n>0n<0
根据如下定理 :
如果 x ( n ) x(n) x(n) 序列 是 " 实序列 " , " 偶对称的 " , 则其傅里叶变换 X ( e j ω ) X(e^{j \omega}) X(ejω) 也是 " 实序列 " , " 偶对称的 " ;
则 x e ( n ) x_e(n) xe(n) 的 傅里叶变换 X R ( e j ω ) X_R(e^{j \omega}) XR(ejω) 也是 实偶 的 ;
下面的序列 x o ( n ) x_o(n) xo(n) 为实奇 ,
x o ( n ) = { 0 n = 0 a n 2 n > 0 − a − n 2 n < 0 x_o(n) =\begin{cases} 0 & n = 0 \\\\ \cfrac{a^n}{2} & n > 0 \\\\ -\cfrac{a^{-n}}{2} & n < 0 \end{cases} xo(n)=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧02an−2a−nn=0n>0n<0
根据如下定理 :
如果 x ( n ) x(n) x(n) 序列 是 " 实序列 " , " 奇对称的 " , 则其傅里叶变换 X ( e j ω ) X(e^{j \omega}) X(ejω) 也是 " 虚序列 " , " 奇对称的 " ;
则 x o ( n ) x_o(n) xo(n) 的 傅里叶变换 j X I ( e j ω ) jX_I(e^{j \omega}) jXI(ejω) 也是 虚奇 的 ;
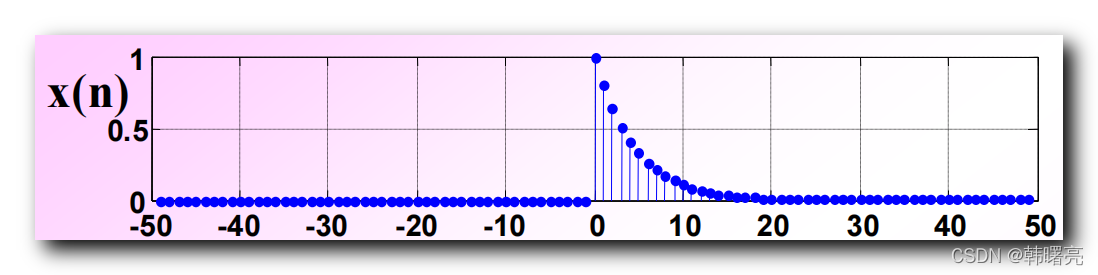
原序列 x ( n ) x(n) x(n) 图像如下 :
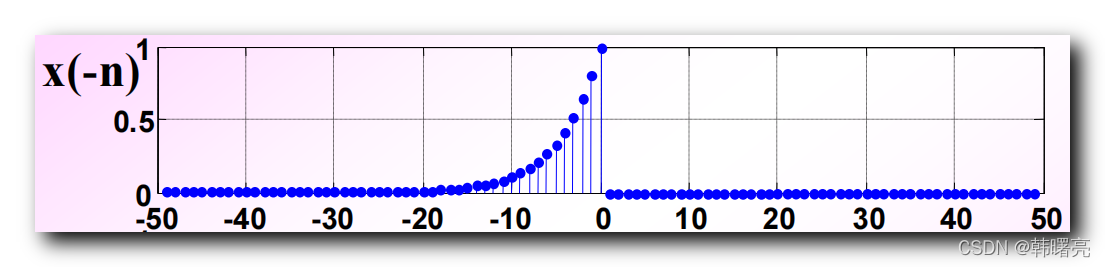
x ( − n ) x(-n) x(−n) 图像 , 就是将 x ( n ) x(n) x(n) 图像 , 以 y y y 轴为中心进行镜像 :
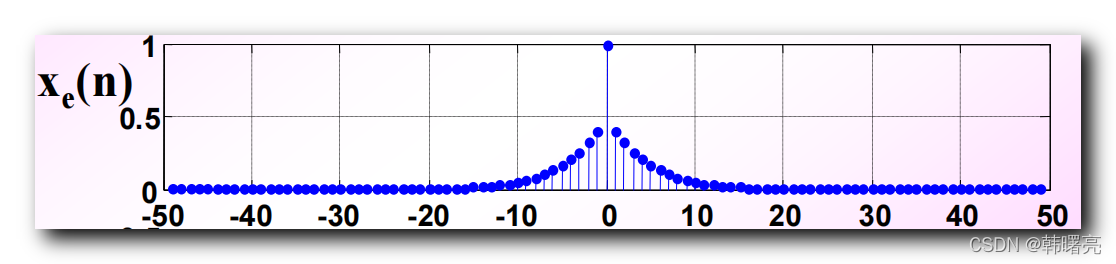
x ( n ) x(n) x(n) 序列的 共轭对称分量 x e ( n ) x_e(n) xe(n) 就是 x ( n ) x(n) x(n) 与 x ( − n ) x(-n) x(−n) 相加 , 除以 2 2 2 :
x e ( n ) = x ( n ) + x ( − n ) 2 x_e(n) = \cfrac{x(n) + x(-n)}{2} xe(n)=2x(n)+x(−n)
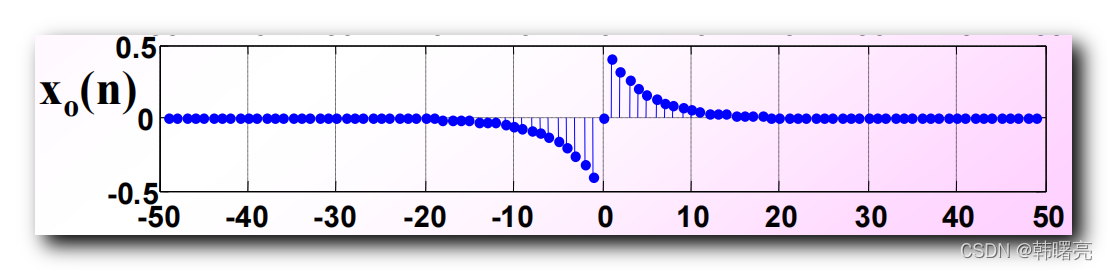
x ( n ) x(n) x(n) 序列的 共轭反对称分量 x o ( n ) x_o(n) xo(n) 就是 x ( n ) x(n) x(n) 与 x ( − n ) x(-n) x(−n) 相减 , 除以 2 2 2 :
x o ( n ) = x ( n ) − x ( − n ) 2 x_o(n) = \cfrac{x(n) - x(-n)}{2} xo(n)=2x(n)−x(−n)
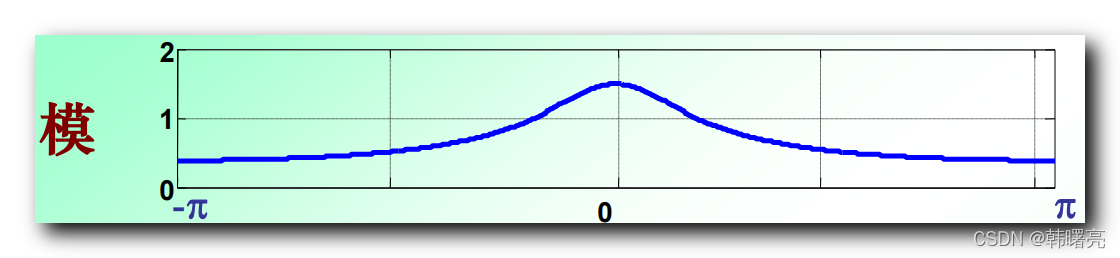
x ( n ) x(n) x(n) 的模 图像如下 , 是偶对称的 ;
x ( n ) x(n) x(n) 的 实部 图像如下 , 是偶对称的 ;
x ( n ) x(n) x(n) 的 虚部 图像如下 , 是奇对称的 ;
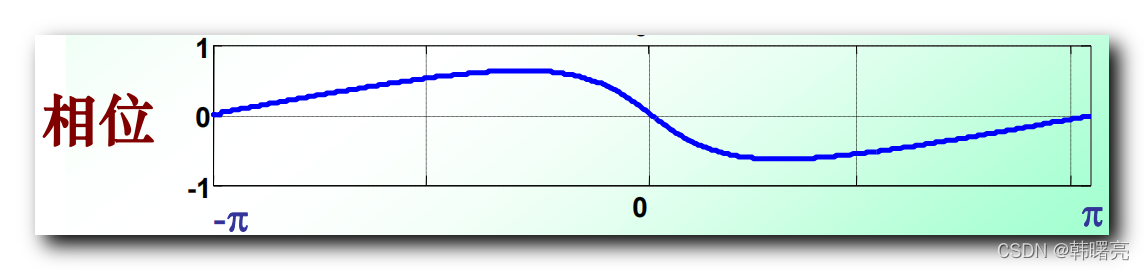
x ( n ) x(n) x(n) 的 相位 图像如下 , 是奇对称的 ;