介绍谱聚类（spectral clustering）

文章目录

- 1、谱聚类概览
- 2、谱聚类构图
- 3、拉普拉斯矩阵
- 4、切图聚类
- 4.1RatioCut
- 4.2Ncut
- 5、总结流程

1、谱聚类概览

谱聚类演化于图论，后由于其表现出优秀的性能被广泛应用于聚类中，对比其他无监督聚类（如kmeans），spectral clustering的优点主要有以下：

1.过程对数据结构并没有太多的假设要求，如kmeans则要求数据为凸集。
2.可以通过构造稀疏similarity graph，使得对于更大的数据集表现出明显优于其他算法的计算速度。
3.由于spectral clustering是对图切割处理，不会存在像kmesns聚类时将离散的小簇聚合在一起的情况。
4.无需像GMM一样对数据的概率分布做假设。

同样，spectral clustering也有自己的缺点，主要存在于构图步骤，有如下：

1.对于选择不同的similarity graph比较敏感（如 epsilon-neighborhood， k-nearest neighborhood，fully connected等）。
2.对于参数的选择也比较敏感（如 epsilon-neighborhood的epsilon，k-nearest neighborhood的k，fully connected的 ）。

谱聚类过程主要有两步，第一步是构图，将采样点数据构造成一张网图，表示为G(V,E)，V表示图中的点，E表示点与点之间的边，如下图：
图1 谱聚类构图(来源wiki)

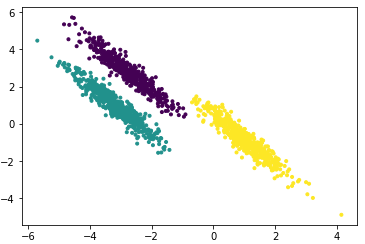
第二步是切图，即将第一步构造出来的按照一定的切边准则，切分成不同的图，而不同的子图，即我们对应的聚类结果，举例如下：
在这里插入图片描述图2 谱聚类切图
总的来说它的主要思想是把所有的数据看做空间中的点，这些点之间可以用边连接起来。距离较远的两个点之间的边权重值较低，而距离较近的两个点之间的边权重值较高，通过对所有数据点组成的图进行切图，让切图后不同的子图间边权重和尽可能的低，而子图内的边权重和尽可能的高，从而达到聚类的目的。

2、谱聚类构图

在构图中，一般有三种构图方式：
1. -neighborhood
2. k-nearest neighborhood
3. fully connected
前两种可以构造出稀疏矩阵，适合大样本的项目，第三种则相反，在大样本中其迭代速度会受到影响制约，在讲解三种构图方式前，需要引入similarity function，即计算两个样本点的距离，一般用欧氏距离：, 表示样本点与的距离，或者使用高斯距离，其中的选取也是对结果有一定影响，其表示为数据分布的分散程度，通过上述两种方式之一即可初步构造矩阵，一般称为Similarity matrix(相似矩阵)。
对于第一种构图 -neighborhood，顾名思义是取的点，则相似矩阵可以进一步重构为邻接矩阵(adjacency matrix) :
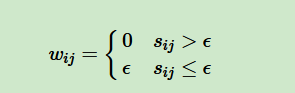
在这里插入图片描述
可以看出，在 ε-neighborhood重构下，样本点之间的权重没有包含更多的信息了。
对于第二种构图k-nearest neighborhood，其利用KNN算法，遍历所有的样本点，取每个样本最近的k个点作为近邻，但是这种方法会造成重构之后的邻接矩阵 W非对称，为克服这种问题，一般采取下面两种方法之一：
一是只要点xi在 xj的K个近邻中或者 xj在 xi的K个近邻中，则保留 $s_{i,j}$ 并对其做进一步处理 W，此时为：

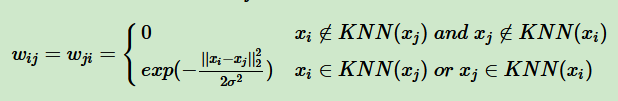
二是必须满足点在的K个近邻中且在的K个近邻中，才会保留 $s_{i,j}$ 并做进一步变换，此时 W为：
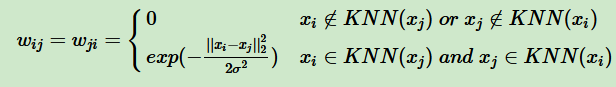在这里插入图片描述对于第三种构图fully connected，一般使用高斯距离： $s_{i,j}=e^{\frac{-\left \| x_{i}-x_{j} \right \|^{2}}{2\sigma ^{2}}}$ ，则重构之后的矩阵 W与之前的相似矩阵S相同，为： $W_{i,j}= S_{i,j}=[s]_{i,j}$ 。
在了解三种构图方式后，还需要注意一些细节，对于第一二中构图，一般是重构基于欧氏距离的，而第三种构图方式，则是基于高斯距离的，注意到高斯距离的计算蕴含了这样一个情况：对于 $\left \| x_{i}-x_{j} \right \|^{2}$ 比较大的样本点，其得到的高斯距离反而值是比较小的，而这也正是 S可以直接作为W的原因，主要是为了将距离近的点的边赋予高权重。
得到邻接矩阵 W后，需要做进一步的处理：
(1).计算阶矩(degree matrix)D：
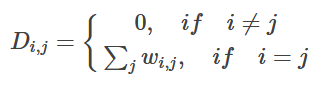
在这里插入图片描述
其中其中 $w_{i,j}$ 为邻接矩阵 W元素， $\sum_{j}w_{i,j}$ 表示将图中某点所连接的其他点的边的权重之和，可以看出， D为对角矩阵.
(2).计算拉普拉斯矩阵(Laplacians matrix)L： L=D−W
如此，在构图阶段基本就完成了，至于为什么要计算出拉普拉斯矩阵 L，可以说L=D−W这种形式对于后面极大化问题是非常有利的。
$W_{i,j}=\left\{\begin{matrix} 0,\quad if \quad s_{i,j}>\varepsilon\\ \varepsilon,\quad if \quad s_{i,j}\leq \varepsilon \end{matrix}\right.$
在实际的应用中，使用第三种全连接法来建立邻接矩阵是最普遍的，而在全连接法中使用高斯径向核RBF是最普遍的。

3、拉普拉斯矩阵

单独把拉普拉斯矩阵(Graph Laplacians)拿出来介绍是因为后面的算法和这个矩阵的性质息息相关。它的定义很简单，拉普拉斯矩阵L=D−W。D即为度矩阵，它是一个对角矩阵。而W拉普拉斯矩阵有一些很好的性质如下：

1）拉普拉斯矩阵是对称矩阵，这可以由D
和W

都是对称矩阵而得。

2）由于拉普拉斯矩阵是对称矩阵，则它的所有的特征值都是实数。

3）对于任意的向量f,我们有
　　　　 $f^TLf = \frac{1}{2}\sum\limits_{i,j=1}^{n}w_{ij}(f_i-f_j)^2$

4、切图聚类

为了避免最小切图导致的切图效果不佳，我们需要对每个子图的规模做出限定，一般来说，有两种切图方式，第一种是RatioCut，第二种是Ncut。下面我们分别加以介绍。
$Ratiocut(A_{1},A_{2},\cdots,A_{k})=\frac{1}{2}\sum_{i}^{k}\frac{W(A_{i},\bar{A_{i}})}{\left | A_{i} \right |}$ $Ncut(A_{1},A_{2},\cdots,A_{k})=\frac{1}{2}\sum_{i}^{k}\frac{W(A_{i},\bar{A_{i}})}{vol(A_{i})}$