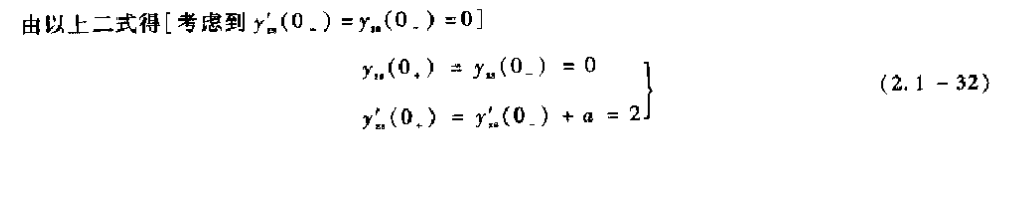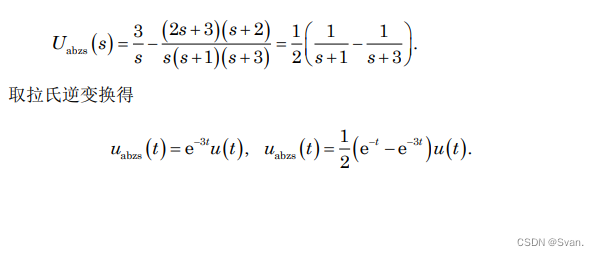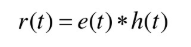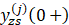(一)零状态响应的定义
零状态响应是系统在初始状态为零时,仅有输入信号 f ( t ) f(t) f(t)引起的响应。用 y z s ( t ) y_{zs}(t) yzs(t)表示
(二)解题步骤
(1)当微分方程右端不含冲击函数 δ ( t ) \delta(t) δ(t)时
- 由于微分方程右端不含冲击函数 δ ( t ) \delta(t) δ(t),所以零状态响应在 t = 0 t=0 t=0时不会发生突变。故 0 − 0_- 0−和 0 + 0_+ 0+时的响应相等。即 y z s ( 0 − ) = y z s ( 0 + ) = 0 y_{zs}(0_-)=y_{zs}(0_+)=0 yzs(0−)=yzs(0+)=0, y z s ′ ( 0 − ) = y z s ′ ( 0 + ) = 0 y'_{zs}(0_-)=y'_{zs}(0_+)=0 yzs′(0−)=yzs′(0+)=0。
- 解微分方程,先求其通解,再求特解,得出 y z s ( t ) y_{zs}(t) yzs(t)的表达式
- 将 f ( 0 + ) f(0_+) f(0+)和 f ′ ( 0 + ) f'(0_+) f′(0+)的值代入 y z s ( t ) y_{zs}(t) yzs(t)的表达式并解出 C C C
- 解出零状态输入响应
(1)当微分方程右端含有冲击函数 δ ( t ) \delta(t) δ(t)时
1.将激励 f ( t ) f(t) f(t)的值代入微分方程中。
2.按照以前的博客——LTI连续系统微分方程解法1——y(0 +)的求法,求出 y z s ( n ) ( 0 + ) y^{(n)}_{zs}(0_+) yzs(n)(0+)d
的值
3.解微分方程,先求其通解,再求特解,得出 y z s ( t ) y_{zs}(t) yzs(t)的表达式
4.将 f ( 0 + ) f(0_+) f(0+)和 f ′ ( 0 + ) f'(0_+) f′(0+)的值代入 y z s ( t ) y_{zs}(t) yzs(t)的表达式并解出 C C C
5. 解出零状态输入响应
微分方程不同激励对应的特解

(三)例题

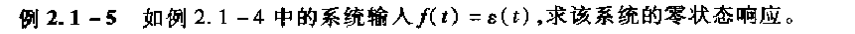
解