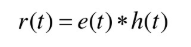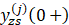题目:
已知系统的微分方程为:
d 2 y ( t ) d t 2 + 2 d y ( t ) d t + 100 y ( t ) = f ( t ) \dfrac{d^2y(t)}{dt^2}+2\dfrac{dy(t)}{dt}+100y(t)=f(t) dt2d2y(t)+2dtdy(t)+100y(t)=f(t)
系统的输入信号为: f ( t ) = 10 s i n ( 2 π t ) f(t)=10sin(2πt) f(t)=10sin(2πt), 求其零状态响应。
这里主要介绍的是lsim函数,在 MATLAB 中使用 lsim 函数时,它会执行一个线性系统的仿真,该系统由一个连续时间系统的传递函数表示。该函数可以用于计算系统对于一个给定的输入信号的响应。其中b和a分别是差分方程(系统函数)的分子和分母,f是系统的输入,t是时间变量。
lsim(b,a,f,t)
完整代码:
t=0:0.001:6;
b=[1];
a=[1,2,100];
f=10*sin(2*pi*t);y=lsim(b,a,f,t);
plot(t,y)
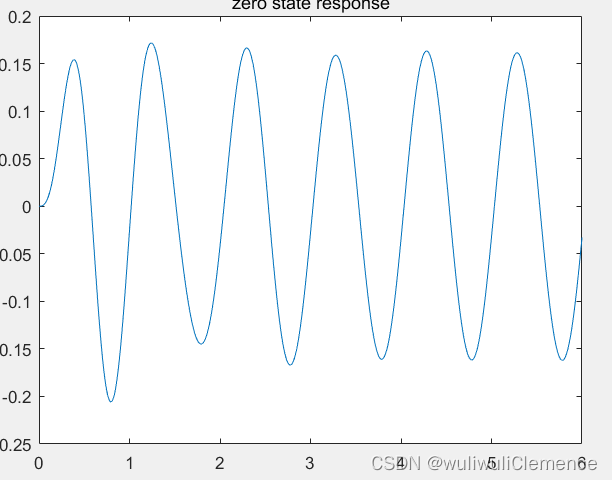
title('zero state response')
运行结果: