一、引子

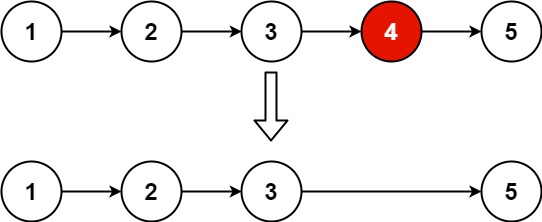
剪枝，就是减小搜索树规模、尽早排除搜索树中不必要的分支的一种手段。

形象地看，就好像剪掉了搜索树的枝条，故被称为剪枝。

二、常见剪枝方法

1.优化搜索顺序

在一些问题中，搜索树的各个分支之间的顺序是不固定的

不同的搜索顺序会产生不同的搜索形态，规模也相差甚远

2.排除等效分支

在搜索过程中，如果我们能够得知搜索树的当前节点沿着

某几条不同分支到达的子树是等效的，那么只需要对其中

一条路径进行搜索

3.是否可行剪枝

在搜索过程中，每次对当前状态进行检查，如果发现不可

能到达递归边界，就执行回溯

4.最优性剪枝

在求解最优解的过程中，如果当前解已经没有当前最优解

优秀，此时可以执行回溯语句

5.记忆化剪枝

记录每个状态的搜索结果，在重复遍历一个状态时返回

三、例题

（一）生日蛋糕 POJ1190

题目描述

Mr.W 要制作一个体积为Nπ 的 M层生日蛋糕，每层都是一个圆柱体。设从下往上数第 i蛋糕是半径为 Ri，高度为 Hi 的圆柱。当 i<Mi<M 时，要求Ri>Ri+1且Hi>Hi+1。由于要在蛋糕上抹奶油，为尽可能节约经费，我们希望蛋糕外表面（最下一层的下底面除外）的面积 Q最小。 令 Q=Sπ ，请编程对给出的 N和M ，找出蛋糕的制作方案（适当的 Ri 和Hi 的值），使 S最小。（除 QQ 外，以上所有数据皆为正整数）

输入

第一行为 N ，表示待制作的蛋糕的体积为Nπ； 

第二行为 M ，表示蛋糕的层数为 M 。 

输出

输出仅一行，一个整数 S（若无解则 S=0 ）。

样例输入

100
2

样例输出

68

提示

附：圆柱相关公式：体积 V=πR2H；侧面积 S’=2πRH；底面积 S=SπR2。

数据范围与提示

对于全部数据，1≤N≤104,1≤M≤20。 

题解：

搜索框架：从下往上搜索，枚举每层的半径和高度作为分支

搜索状态：第dep层，当前外表面积s,当前体积v,dep+1层的高度和半径

整个蛋糕的底面积=最底层的圆面积，这样在m-1层搜索时，只需要计算侧面积

剪枝：

1.是否可行剪枝

首先枚举

其次枚举

2.优化搜索顺序

倒序搜索枚举

3.可行性剪枝

预处理最小体积和侧面积，然后剪枝

#include <bits/stdc++.h>
using namespace std;
int n,m;
int ans=2e9;
void dfs(int dep,int s,int v,int past_r,int past_h)
{if(s >= ans) return;if(dep == m+1 && v == n){ans = min(ans,s);return;}if(v >= n) return;int rest_dep = m - dep + 1;if(rest_dep * past_r * past_r * past_h + v < n) return;if(dep == 1){for(int r = past_r; r >= m; --r)for(int h = m; h <= past_h; ++h)dfs(dep + 1,s + r * r + 2 * r * h,v + r * r * h,r,h);}else{for(int r=past_r-1; r>=m-dep+1; --r)for(int h=m-dep+1; h<past_h; ++h)dfs(dep + 1,s + 2 * r * h,v + r * r * h,r,h);}
}
int main()
{scanf("%d%d",&n,&m);dfs(1,0,0,28,28);if(ans == 2e9) printf("0\n");else printf("%d\n",ans);
}

（二）Sticks POJ1011

题目描述

乔治有一些同样长的小木棍，他把这些木棍随意砍成几段，直到每段的长都不超过 50。现在，他想把小木棍拼接成原来的样子，但是却忘记了自己开始时有多少根木棍和它们的长度。给出每段小木棍的长度，编程帮他找出原始木棍的最小可能长度。 

输入

第一行为一个单独的整数N表示砍过以后的小木棍的总数。 第二行为 N个用空格隔开的正整数，表示N根小木棍的长度。

输出

输出仅一行，表示要求的原始木棍的最小可能长度。

样例输入

9
5 2 1 5 2 1 5 2 1

样例输出

6

提示

数据范围与提示

1≤N≤60

题解：

我们可以从大到小枚举原始木棒的长度len.而len应该是sum的约数

原始木棒的根数cnt=sum/len

对于枚举的每个len,我们可以依次搜索每根原始木棒由哪些木棍组成

搜索顺序：从大到小

搜索状态：正在拼的木棍序号、木棒长度、现在拼好的长度、现在拼好的木棒根数

剪枝

1.优化搜索顺序

从大到小排序，优先尝试长的木棍

2.排除等效分支

(1).因为先拼一根a长度的，再拼一根b长度的等于

先拼一根b长度的，再拼一根a长度,只要搜索其中一种

(2).记录最近一次尝试拼接的木棍长度，如果搜索失败则不尝试

同种长度的木棍

(3).当尝试拼入的第一根木棍就返回失败，则直接回溯

(4).如果当前木棍拼入后，一节木棒被填充完整，而另一根木棍

失败了，则直接回溯

代码：

#include<bits/stdc++.h>
#define MAXN 100005
using namespace std;
int n,sum=0,a[MAXN];
bool vis[MAXN]; 
int cmp(int a,int b)
{return a>b;
}
bool dfs(int num,int len,int now_len,int number)
{if(number==sum/len)return 1;if(now_len==len){if(dfs(1,len,0,number+1))return 1;}for(int i=num; i<=n; i++){if(!vis[i]&&now_len+a[i]<=len){vis[i]=true;if(dfs(i+1,len,now_len+a[i],number))return 1;vis[i]=false;if(a[i]==len-now_len||now_len==0)break;while(a[i]==a[i+1])i++; }}return 0;
}
int main()
{memset(vis,false,sizeof(vis));scanf("%d",&n);for(int i=1; i<=n; i++){scanf("%d",&a[i]);sum+=a[i];}sort(a+1,a+1+n,cmp);for(int i=a[1]; i<=sum; i++){if(sum%i!=0)continue;if(dfs(1,i,0,0)){cout<<i<<endl;break;}}
}