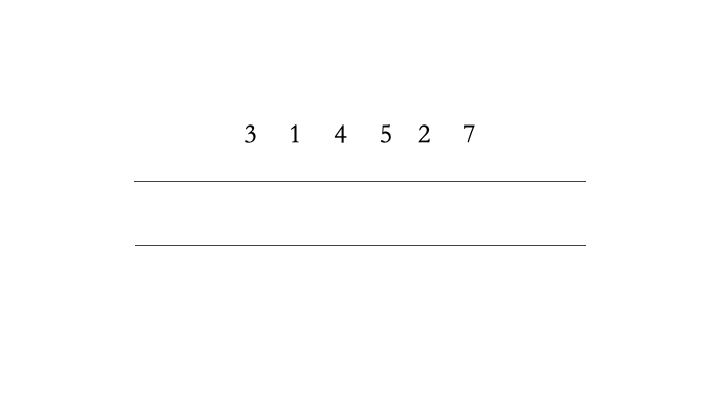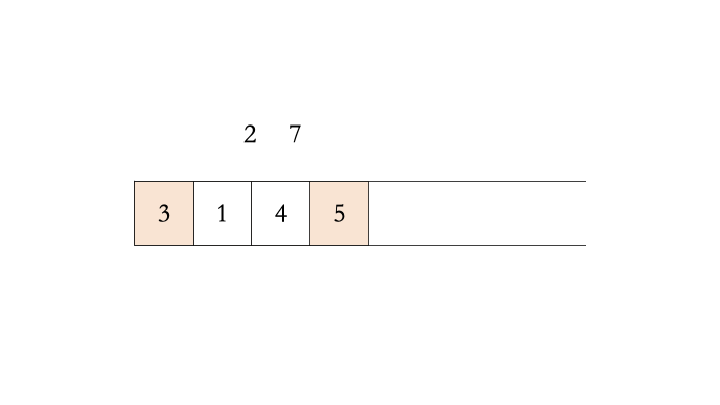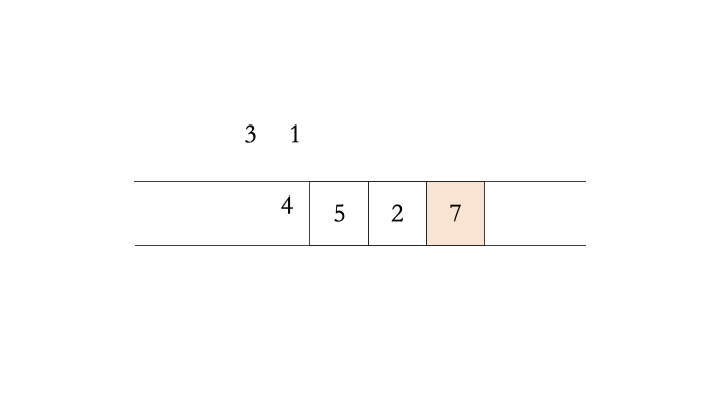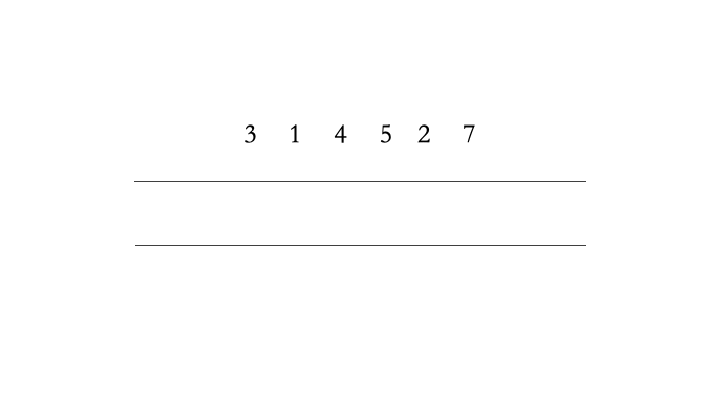优先队列简介
优先队列(priority queue)可以在 O(1) 时间内获得最大值,并且可以在 O(log n) 时间内取出最大值或插入任意值。
优先队列常常用堆(heap)来实现。堆是一个完全二叉树,其每个节点的值总是大于等于子节点的值。实际实现堆时,我们通常用一个数组而不是用指针建立一个树。这是因为堆是完全二叉树,所以用数组表示时,位置 i 的节点的父节点位置一定为 i/2,而它的两个子节点的位置又一定分别为 2i 和 2i+1。
以下是堆的实现方法,其中最核心的两个操作是上浮和下沉:如果一个节点比父节点大,那么需要交换这个两个节点;交换后还可能比它新的父节点大,因此需要不断地进行比较和交换操作,我们称之为上浮;类似地,如果一个节点比父节小,也需要不断地向下进行比较和交换操作,我们称之为下沉。如果一个节点有两个子节点,我们总是交换最大的子节点。
vector<int> heap;
// 获得最大值
void top() {return heap[0];
}
// 插入任意值:把新的数字放在最后一位,然后上浮
void push(int k) {heap.push_back(k);swim(heap.size() - 1);
}
// 删除最大值:把最后一个数字挪到开头,然后下沉
void pop() {heap[0] = heap.back();heap.pop_back();sink(0);
}
// 上浮
void swim(int pos) {while (pos > 1 && heap[pos/2] < heap[pos])) {swap(heap[pos/2], heap[pos]);pos /= 2;}
}
// 下沉
void sink(int pos) {while (2 * pos <= N) {int i = 2 * pos;if (i < N && heap[i] < heap[i+1]){++i;}if (heap[pos] >= heap[i]){break;} swap(heap[pos], heap[i]);pos = i;}
}
通过将算法中的大于号和小于号互换,我们也可以得到一个快速获得最小值的优先队列。
另外,正如我们在 STL 章节提到的那样,如果我们需要在维持大小关系的同时,还需要支持查找任意值、删除任意值、维护所有数字的大小关系等操作,可以考虑使用 set 或 map 来代替优先队列。
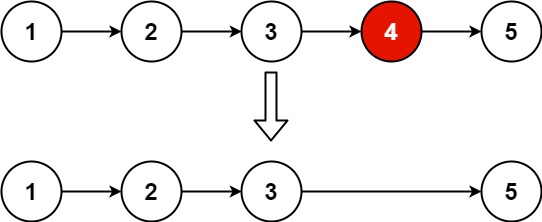
23. 合并K个升序链表
给定一个链表数组,每个链表都已经按升序排列。请将所有链表合并到一个升序链表中,返回合并后的链表。
输入是一个一维数组,每个位置存储链表的头节点;输出是一条链表。
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组:[1->4->5, 1->3->4, 2->6] 将它们合并到一个有序链表中得到:1->1->2->3->4->4->5->6
解析:
本题我们可以采用STL中的容器适配器 priority_queue,把所有的链表存储在一个优先队列中,每次提取所有链表头部节点值最小的那个节点,直到所有链表都被提取完为止。
需要注意的是 priority_queue 默认的元素比较方法是less<T>,即默认为最大值元素在前面的最大堆,维持着递增关系。如果我们想要获取最小的节点值,则需要实现一个最小堆,因此比较函数应该维持递减关系。实现侧策略就是使用函数对象,自定义 priority_queue 的元素比较方法,在该函数对象中重载 operator() ,使用大于号而不是等增关系时的小于号进行比较。
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/struct MyCompare{bool operator() (ListNode* a, ListNode* b){return a->val > b->val;}
};class Solution {
public:ListNode* mergeKLists(vector<ListNode*>& lists) {if(lists.empty()) return nullptr;// 自定义优先队列的元素比较方法 MyComparepriority_queue<ListNode*, vector<ListNode*>, MyCompare> pq;// 将lists都压入到优先队列中,保持递减关系for(const auto list: lists){if(list){pq.push(list);}}// 每次取出所有链表中头部节点最小的那个节点加入结果链表ListNode head; ListNode* tail = &head;while(!pq.empty()){// 取出所有链表中的最小头节点并加入 结果链表tail->next = pq.top();pq.pop();tail = tail->next;// 加入后,将其 next 节点作为当前链表的新头节点加入优先队列if(tail->next){pq.push(tail->next);}}return head.next;}
};
本题也可以采用归并排序的思想,将链表两两合并。
根据分治策略,首先要将 k 个链表分割,使用递归的方法将链表分割为两两一组。然后将在同一个组的链表合并。
合并两个有序链表可以通过如下操作实现:
- 首先需要一个变量 head 来保存合并之后链表的头部,在整个链表合并完之后,返回 head 的下一位置即可。
- 需要一个指针 tail 来记录下一个插入位置的前一个位置,以及两个指针 aPtr 和 bPtr 来记录 a 和 b 未合并部分的第一位,即通过尾插法构建新链表
- 当 aPtr 和 bPtr 都不为空的时候,取 val 熟悉较小的合并;如果 aPtr 为空,则把整个 bPtr 以及后面的元素全部合并;bPtr 为空时同理。
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeTowList(ListNode* a, ListNode* b){if(!a || !b) return a?a:b;// 变量 head 来保存合并之后链表的头部ListNode head;ListNode* tail = &head;ListNode* aPtr = a;ListNode* bPtr = b;while(aPtr && bPtr){if(aPtr->val <= bPtr->val){tail->next = aPtr;aPtr = aPtr->next;}else{tail->next = bPtr;bPtr = bPtr->next;}tail = tail->next;}// 循环结束 aPtr 和 bPtr 其中一个为空,直接将非空的添加到链表if(aPtr){tail->next = aPtr;}else{tail->next = bPtr;}return head.next;}ListNode* merge(vector<ListNode*>& lists, int lsh, int rsh){if(lsh == rsh){return lists[lsh];}if(lsh > rsh){return nullptr;}int mid = (lsh + rsh) >> 1;ListNode* lshList = merge(lists,lsh,mid);ListNode* rshList = merge(lists,mid+1,rsh);return mergeTowList(lshList,rshList);}ListNode* mergeKLists(vector<ListNode*>& lists) {return merge(lists,0,lists.size()-1);}
};
218 天际线问题
给定建筑物的起止位置和高度,返回建筑物轮廓(天际线)的拐点。
输入是一个二维整数数组,表示每个建筑物的 [左端, 右端, 高度];输出是一个二维整数数组,表示每个拐点的横纵坐标。

输入:buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
输出:[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
解释:图 A 显示输入的所有建筑物的位置和高度,图 B 显示由这些建筑物形成的天际线。图 B 中的红点表示输出列表中的关键点。
解析:
本题没搞懂,有待再理解
我们可以使用优先队列储存每个建筑物的高度和右端(这里使用 pair,其默认比较函数是先比较第一个值,如果相等则再比较第二个值),从而获取目前会拔高天际线、且妨碍到前一个建筑物(的右端端点)的下一个建筑物。
class Solution {
public:vector<vector<int>> getSkyline(vector<vector<int>>& buildings) {vector<vector<int>> ans;priority_queue<pair<int,int>> heap;int i = 0;int len = buildings.size();int cur_x, cur_h;while(i<len || !heap.empty()){if(heap.empty() || i<len && buildings[i][0] <= heap.top().second){cur_x = buildings[i][0];while(i<len && cur_x==buildings[i][0]){heap.emplace(buildings[i][2], buildings[i][1]);++i;}}else{cur_x = heap.top().second;while(!heap.empty() && cur_x >= heap.top().second){heap.pop();}}cur_h = (heap.empty())?0:heap.top().first;if(ans.empty() || cur_h != ans.back()[1]){ans.push_back({cur_x,cur_h});}}return ans;}
};
870 优势洗牌
给定两个大小相等的数组 A 和 B,A 相对于 B 的优势可以用满足 A[i] > B[i] 的索引 i 的数目来描述。
返回 A 的任意排列,使其相对于 B 的优势最大化。
输入:A = [12,24,8,32], B = [13,25,32,11]
输出:[24,32,8,12]
解析:
本题采用田忌赛马的策略,如果 A 中有元素比 B 的大,那么用最大的那个值取对应B中的元素;如果A中没有元素比当前B大,那么用最小的 A 对应该元素。
我们采用优先队列保存 B 中的元素值和原先位置,并维持递减顺序。将 A 中元素按递增排序,然后遍历优先队列中的 B 元素。因为B采用优先队列保存,所以取出的总是当前B的最大元素,如果 A 中存在比该元素还大的值,则取 A 的当前最大值即排序后数组末尾元素放在该元素的原先位置;不存在就用 A 中的最小元素即排序后数组第一个元素放在该元素的原先位置。
例如A = [12,24,8,32], B = [13,25,32,11],对A排序,对B用优先队列存储元素值和原先位置有A = [8,12,24,32], B = [{32,2},{25,1},{13,0},{11,3}],结果形成过程如下:
| sort_A | priority_queue_B | result_A |
|---|---|---|
[8,12,24,32] | [{32,2},{25,1},{13,0},{11,3}] | [0,0,0,0] |
[12,24,32] | [{25,1},{13,0},{11,3}] | [0,0,8,0] |
[12,24] | [{13,0},{11,3}] | [0,32,8,0] |
[12] | [{11,3}] | [24,32,8,0] |
[] | [{}] | [24,32,8,12] |
class Solution {
public:vector<int> advantageCount(vector<int>& nums1, vector<int>& nums2) {vector<int> ans(nums1.size());// A 排序sort(nums1.begin(),nums1.end());// B 用优先队列保存priority_queue<pair<int,int>> pq;for(int i=0;i<nums2.size();++i){pq.push(make_pair(nums2[i],i));}// 逐个比较优先队列中的元素,根据大取大、小取小的原则洗牌A的元素int head = 0, tail = nums1.size()-1;while(!pq.empty()){int num = pq.top().first;int index = pq.top().second;pq.pop();if(nums1[tail]>num){ans[index] = nums1[tail--];}else{ans[index] = nums1[head++];}}return ans;}
};
参考资料
LeetCode 101:和你一起轻松刷题(C++) 第 11 章 妙用数据结构

![[算法] 栈和队列](https://img-blog.csdnimg.cn/ce7df0be33f0470fb7d74a4b449cb342.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA6KW_56eR6IOh5YWI55Sf,size_20,color_FFFFFF,t_70,g_se,x_16)