栈和队列相关经典算法题总结(数据结构+C语言)

article/2025/9/16 2:57:31

我们这里针对栈和队列的一些经典算法题做详细讲解:

1.括号匹配问题.

2.用队列实现栈.

3.用栈实现队列.

4.设计循环队列.

一.详细讲解如下:

1.括号匹配问题.(如下图)

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。有效字符串需满足：左括号必须用相同类型的右括号闭合。左括号必须以正确的顺序闭合。(试题来源力扣)

//判断括号是否匹配
bool isValid(char * s){if(NULL==s){//判空return false;}if('}'==s[0] || ']'==s[0] || ')'==s[0]){//判断是否只有一个元素return false;}int i=0;Stack St;StackInit(&St);//创建和初始化栈while(s[i]!='\0'){if('['==s[i] || '{'==s[i] || '('==s[i]){//为左括号的就入栈StackPush(&St,s[i]);}else{//不是左括号就与栈顶元素作比较,为一组就出栈继续向后走,不为一组直接返回false.if((StackTop(&St)=='[' && ']'==s[i])||(StackTop(&St)=='(' && ')'==s[i])||(StackTop(&St)=='{' && '}'==s[i])){StackPop(&St);}else{return false;}}i++;}if(0==StackSize(&St)){//如果循环走完并且栈为空说明所有括号都可以匹配,直接返回true.return true;}return false;//否则返回false.
}

2.用队列实现栈.

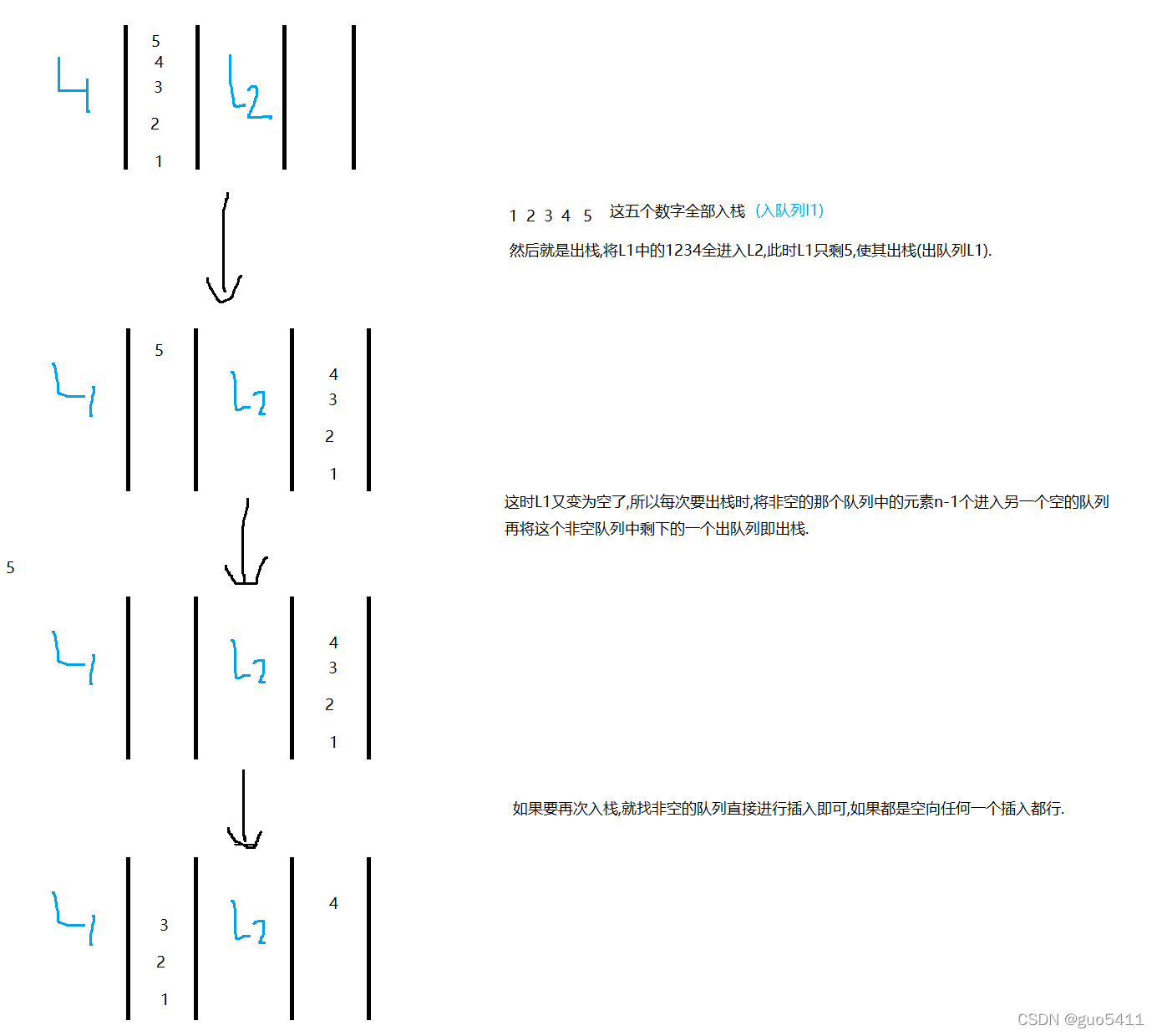
使用两个队列来对栈进行实现:首先我们得知道队列是"先进先出"的一个特性所以我们就可以利用它这个特性来实现栈(后进先出),入栈时我们可以把所有元素全放进一个队列中,出栈时将这个有元素的队列中的元素只留一个剩下的全进入另一个空的队列,此时留在队列中的这个元素就是最后一个进入队列的元素也就是最后一个入栈的元素,令它出队列,也就是出栈,然后重复上面的操作就完成了对栈的实现.(如下图)

//实现栈
typedef struct {Queue q1;Queue q2;
} MyStack;
//创建栈的结构体
MyStack* myStackCreate() {MyStack* l=(MyStack*)malloc(sizeof(MyStack));if(NULL==l){printf("申请失败!\n");return NULL;}QueueInit(&(l->q1));QueueInit(&(l->q2));return l;
}
//入栈
void myStackPush(MyStack* obj, int x) {if(NULL==obj){return;}if(obj->q1._front==obj->q1._rear){QueuePush(&(obj->q2),x);    }else{QueuePush(&(obj->q1),x);}
}
//出栈
int myStackPop(MyStack* obj) {if(1==_myStackEmpty(obj)){return NULL;}int data=0;if(obj->q1._front==obj->q1._rear){while(obj->q2._rear!=obj->q2._front->_next){QueuePush(&(obj->q1),QueueFront(&(obj->q2)));QueuePop(&(obj->q2));}data=obj->q2._rear->_data;QueuePop(&(obj->q2));}else{while(obj->q1._rear!=obj->q1._front->_next){QueuePush(&(obj->q2),QueueFront(&(obj->q1)));QueuePop(&(obj->q1));}data=obj->q1._rear->_data;        QueuePop(&(obj->q1));}return data;
}
//取栈顶元素
int myStackTop(MyStack* obj) {if(1==_myStackEmpty(obj)){return NULL;}if(obj->q1._front==obj->q1._rear){return QueueBack(&(obj->q2));}else{return QueueBack(&(obj->q1));}
}
//判空
int _myStackEmpty(MyStack* obj){if(NULL==obj){return 1;}if(obj->q1._front==obj->q1._rear && obj->q2._front==obj->q2._rear){return 1;}return 0;
}
//栈判空
bool myStackEmpty(MyStack* obj) {if(NULL==obj){return true;}if(obj->q1._front==obj->q1._rear && obj->q2._front==obj->q2._rear){return true;}return false;
}
//销毁栈
void myStackFree(MyStack* obj) {if(NULL==obj){return;}free(obj);obj=NULL;
}

3.用栈实现队列.

与用队列实现栈相似,也是使用两个栈的后进先出的特点来实现队列,入队列时选定一个栈用来做入队列的栈(记作S1)(另一个空队列记作S2),只要时入队列的元素直接插入S1,然后就是出队列,元素总数记作n,将S1中的n-1个元素全进入S2中,然后将S1中剩下的一个元素取出便是出队列,之后再将S2中的元素再次全放入S1中,使S2继续保持空的状态,之后的出队列入队列重复前面两项操作就行.(如下图)

//用栈实现队列
typedef struct {Stack s1;Stack s2;
} MyQueue;
//创建队列的结构体(两个栈)
MyQueue* myQueueCreate() {MyQueue* _queue=(MyQueue*)malloc(sizeof(MyQueue));if(NULL==_queue){printf("申请失败!\n");return NULL;}StackInit(&(_queue->s1));StackInit(&(_queue->s2));return _queue;
}// 判空
int isQueueEmpty(MyQueue* obj){if(NULL==obj){return 1;}if(0==obj->s1._top && 0==obj->s2._top){return 1;}return 0;
}
//入队列
void myQueuePush(MyQueue* obj, int x) {if(NULL==obj){printf("结构体不存在!\n");return;}StackPush(&(obj->s1),x);
}
//出队列
int myQueuePop(MyQueue* obj) {if(isQueueEmpty(obj)){return NULL;}int data=0;while(obj->s1._top!=0){StackPush(&(obj->s2),StackTop(&(obj->s1)));StackPop(&(obj->s1));}data=StackTop(&(obj->s2));StackPop(&(obj->s2));while(obj->s2._top!=0){StackPush(&(obj->s1),StackTop(&(obj->s2)));StackPop(&(obj->s2));}return data;
}
//返回队列的头元素
int myQueuePeek(MyQueue* obj) {if(isQueueEmpty(obj)){return NULL;}int data=0;while(obj->s1._top!=0){StackPush(&(obj->s2),StackTop(&(obj->s1)));StackPop(&(obj->s1));}data=StackTop(&(obj->s2));while(obj->s2._top!=0){StackPush(&(obj->s1),StackTop(&(obj->s2)));StackPop(&(obj->s2));}return data;    
}
//判空
bool myQueueEmpty(MyQueue* obj) {if(NULL==obj){return true;}if(0==obj->s1._top){return true;}return false;
}
//销毁队列
void myQueueFree(MyQueue* obj) {if(NULL==obj){return;}free(obj);obj=NULL;
}

4.设计循环队列.

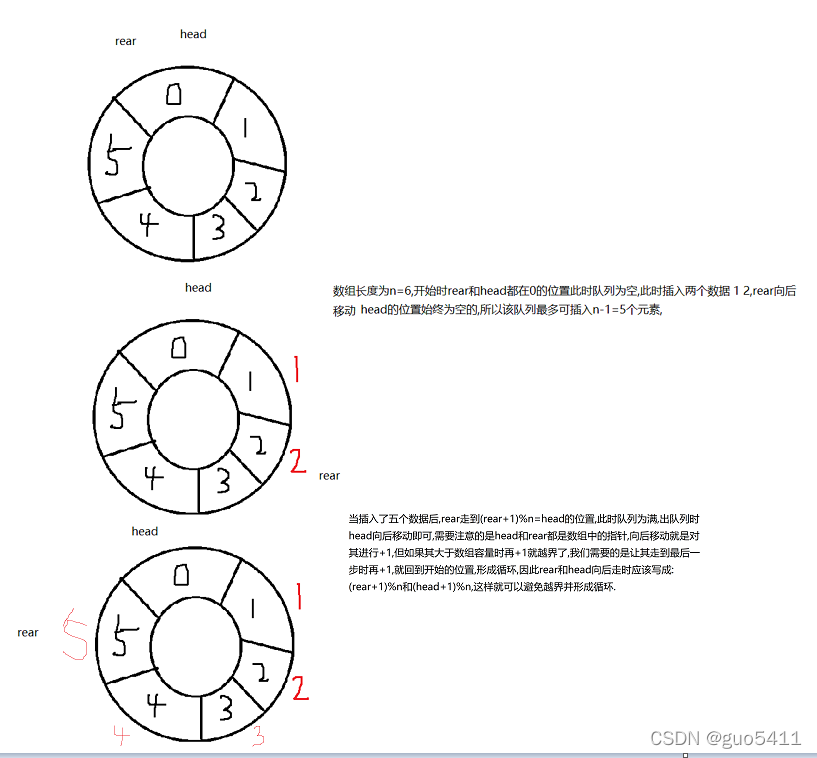
我们使用数组,外加Head和Rear两个首尾指针来创建循环队列,队列的大小提前给好为n,入队列时让Rear移动插入数据,Head移动出队列,当Head等于Rear时队列为空,当(Rear+1)%n等于Head时队列为满.(如图)

//定义结构体使用动态数组
typedef struct {int* _loop_queue_list;int _head;int _rear;int _capacity;    
} MyCircularQueue;
//创建循环链表
MyCircularQueue* myCircularQueueCreate(int k) {MyCircularQueue* _loop_queue=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));if(NULL==_loop_queue){printf("申请失败!\n");return NULL;}_loop_queue->_head=0;_loop_queue->_rear=0;_loop_queue->_capacity=k+1;_loop_queue->_loop_queue_list=(int*)malloc(sizeof(int)*(k+1));return _loop_queue;
}
//判满
int isFull(MyCircularQueue* obj){if((obj->_rear+1)%(obj->_capacity)==(obj->_head)){return 1;}return 0;
}
//判空
int isEmpty(MyCircularQueue* obj){if(obj->_head==obj->_rear){return 1;}return 0;
}
//入队列
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {if(isFull(obj)){return false;}obj->_rear=(obj->_rear+1)%(obj->_capacity);obj->_loop_queue_list[obj->_rear]=value;return true;
}
//出队列
bool myCircularQueueDeQueue(MyCircularQueue* obj) {if(isEmpty(obj)){return false;}obj->_head=(obj->_head+1)%(obj->_capacity);obj->_loop_queue_list[obj->_head]=-1;return true;
}
//获取队列首元素
int myCircularQueueFront(MyCircularQueue* obj) {if(isEmpty(obj)){return -1;}return obj->_loop_queue_list[(obj->_head+1)%(obj->_capacity)];
}
//获取队列尾元素
int myCircularQueueRear(MyCircularQueue* obj) {if(isEmpty(obj)){return -1;}return obj->_loop_queue_list[obj->_rear];
}
//队列判空
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {if(NULL==obj){return true;}if(obj->_head==obj->_rear){return true;}return false;
}
//队列判满
bool myCircularQueueIsFull(MyCircularQueue* obj) {if(NULL==obj){return true;}if((obj->_rear+1)%(obj->_capacity)==(obj->_head)){return true;}return false;
}
//销毁队列
void myCircularQueueFree(MyCircularQueue* obj) {if(NULL==obj){return;}free(obj);obj=NULL;
}


http://chatgpt.dhexx.cn/article/ad26sHRg.shtml

相关文章

qt使用消息队列服务器,qt代码实现消息队列通信

qt使用消息队列服务器,qt代码实现消息队列通信

qt代码实现消息队列通信 内容精选 换一换 HBase 1.X版本在RPC流程中，多个数据通信线程会争抢同一个缓存Buffer队列，代码以lock重入锁实现线程安全，锁抢占严重，导致HBase不能充分发挥CPU多核的能力。HBase 1.X版本的RPC通信机制中B…
阅读更多...
消息队列MQ常见面试题

消息队列MQ常见面试题

面试官在面试候选人时，如果发现候选人的简历中写了在项目中使用了 MQ 技术（如 Kafka、RabbitMQ、RocketMQ），基本都会抛出一个问题：在使用 MQ 的时候，怎么确保消息 100% 不丢失？ 这个问题在实际…
阅读更多...
RabbitMQ消息队列常见面试题总结

RabbitMQ消息队列常见面试题总结

1、什么是消息队列： 1.1、消息队列的优点： （1）解耦：将系统按照不同的业务功能拆分出来，消息生产者只管把消息发布到 MQ 中而不用管谁来取，消息消费者只管从 MQ 中取消息而不管是谁发布的。消息…
阅读更多...
【消息队列】面试题及答案整理

【消息队列】面试题及答案整理

消息队列面试题 为什么要使用消息队列/消息队列的应用场景使用了消息队列会有什么缺点如何保证消息队列是高可用的RocketMQ是如何保证消息队列是高可用的 如何保证消息不被重复消费/如何保证消息消费的幂等性如何保证消费的可靠性传输RocketMQ如何保证消费的可靠性传输RabbitMQ…
阅读更多...
JAVA——快速排序（详细）

JAVA——快速排序（详细）

JAVA快速排序的实现 快速排序由于排序效率在同为O(N*logN)的几种排序方法中效率较高，因此经常被采用，再加上快速排序思想----分治法也确实实用，因此很多软件公司的笔试面试，包括像腾讯，微软等知名IT公司都喜欢考这个&…
阅读更多...
快速排序算法（java实现）

快速排序算法（java实现）

基本思想 快速排序是一种采用分治法解决问题的一个典型应用，也是冒泡排序的一种改进。它的基本思想是，通过一轮排序将待排记录分割成独立的两部分，其中一部分均比另一部分小，则可分别对这两部分继续进行排序，已达到整…
阅读更多...
java快速排序（含快速排序代码）

java快速排序（含快速排序代码）

目录 一：快速排序思想 二：快速排序代码（pivot一定时先和arrays【r】先比较） 三：结果 一：快速排序思想 假设我们现在对“6 1 2 7 9 3 4 5 10 8”这个10个数进行排序。首先在这个序列中随便找一个数作为基准…
阅读更多...
快速排序 Java 实现

快速排序 Java 实现

概念 快速排序（Quicksort）是对冒泡排序的一种改进。 参考: [数据结构与算法(Kotlin语言)]1.冒泡排序（Bubble Sort） 快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法(…
阅读更多...
java快速排序详解

java快速排序详解

文章目录 一、快排原理二、实例操作三、实战代码四、总结 一、快排原理 从待排序区间选择一个数，作为基准值（pivot）；遍历整个待排序区间，将比基准值小的（可等于）放到基准值左边，将比…
阅读更多...
快速排序Java

快速排序Java

基本思想 快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。 算法描述 快速排序使用分治法来把一个串&…
阅读更多...
快速排序 Java模板

快速排序 Java模板

快速排序Java模板 详情参考 https://www.acwing.com/problem/content/787/ https://www.acwing.com/solution/content/2096/ 快速排序的整体过程，动态变化流程 以从小到大排序为例 选择一个目标参考值 p i v i t pivit pivit，通常课本上会说选择数组…
阅读更多...
java 实现快速排序

java 实现快速排序

1.介绍 快速排序是对冒泡排序的一种改进。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一 部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序 过程可以…
阅读更多...
使用 Java 实现快速排序（详解）

使用 Java 实现快速排序（详解）

一、概述 最近在看一些面试题，发现很多面试过程中都会要求手写快速排序，查阅一些博客发现别人写的并不是特别清楚而且也很难记住，所以为了更好的掌握这个算法，所以在这篇文章中，将自己的学习过程记录下来，…
阅读更多...
【JAVA】快速排序

【JAVA】快速排序

快排，和冒泡排序一样，是同一类型的排序，都是交换排序 交换，涉及在遍历中比较，然后相互交换元素 冒泡排序是根据趟数两两比较，边比较边交换，快排也一样，不过冒泡是以顺序表的格式进…
阅读更多...
快速排序Java代码实现

快速排序Java代码实现

代码实现（附注释） import java.util.Arrays;public class Main {public static void main(String[] args) {int[] arr {9, 3, 7, 3, 6, 5, 3, 2, 1, 0};System.out.println("排序前：");System.out.println(Arrays.toString(arr))…
阅读更多...
java 算法之快速排序

java 算法之快速排序

1、快速排序是一种比较高效的排序算法，采用“分而治之”的思想，通过多次比较和交换来实现排序，在一趟排序中把将要排序的数据分成两个独立的部分，对这两部分进行排序使得其中一部分所有数据比另一部分都要小，然后继续递…
阅读更多...
快速排序（java实现）

快速排序（java实现）

高快省的排序算法 有没有既不浪费空间又可以快一点的排序算法呢？那就是“快速排序”啦！光听这个名字是不是就觉得很高端呢。 假设我们现在对“6 1 2 7 9 3 4 5 10 8”这个10个数进行排序。首先在这个序列中随便找一个数作为基准数（不要被这…
阅读更多...
(论文阅读）图像超分辨率的回顾与展望

(论文阅读）图像超分辨率的回顾与展望

(论文阅读）图像超分辨率的回顾与展望 1 引言2 超分辨率技术的分类2.1 多图像超分辨率2.2 视频超分辨率2.3 单图像超分辨率2.3.1 基于插值的单图像超分辨率算法2.3.2 基于重建模型的单图像超分辨率算法2.3.3 基于学习的单图像超分辨率算法 3 基于深度学习的单图像超分…
阅读更多...
【图像超分辨率重建】——EnhanceNet论文精读笔记

【图像超分辨率重建】——EnhanceNet论文精读笔记

2017-EnhanceNet: Single Image Super-Resolution Through Automated Texture Synthesis(EnhanceNet) 基本信息 作者： Mehdi S. M. Sajjadi Bernhard Scholkopf Michael Hirsch 期刊： ICCV 引用： * 摘要： 单一图像超分辨率是指从…
阅读更多...
图像超分辨率

图像超分辨率

参考：https://zhuanlan.zhihu.com/p/31664818 SRCNN: 《Learning a Deep Convolutional Network for Image Super-Resolution》 网络框架为：9*9*64(f19,n164),1*1*32(n232),5*5*1(f35) 所用的损失函数为： 该网络和传统方法的稀疏编码来超分…
阅读更多...
推荐文章

Copyright @ 2022~2023