阅读博客的朋友可以观看视频:
http://study.163.com/course/courseMain.htm?courseId=1002942008
我们聚焦于一道亚马逊的算法面试题,通过分析该题,复盘它的解题情景,我们可以初步体会到算法面试的应对步骤,并从中窥探到,成功的算法面试,其流程应该怎么走。题目如下:
给定一家公司在四十日内的股票走势信息,这些信息包括了它每天交易的最高价,最低价,以及开盘价。假定你做为交易员,必须在股票开盘时做出买入或卖出的决定,你负责设计一个算法用来决定买入和卖出的策略,使得交易获得最高的利润。
拿到问题后,我们不能急于动手写代码,首先要做的第一步是:搞清题意。例如,你要向面试官问清楚股票价格的数据格式,它是存储在数组中,队列中,还是以某种格式存储在文件中。通过与面试官交流,屡清楚题目的真实内容,去除模糊不清的地方,将向面试官传达出你心思慎密的特点。假定,数据的输入格式是整形数组,分别为 L, H, S, 他们分别代表股票从某个阶段开始那天到结束那天的最低价,最高价, 以及开盘价。由于题意要求,股票必须在开盘时做出交易,因此,我们只需要考虑处理S数组中的数据。
一开始,你可能没什么思路,于是倾向于认为,只要把S数组中最大值和最小值的差返回就可以了。于是你把这个做法在一些测试用例中测试一下,例如:
S: 10, 4, 8, 7 , 9, 6, 2, 5, 3
里面的最大值是10,最小值是3, 于是你的算法返回7 = 10 – 3。
然而这么做,违反了题意要求,因为你必须买进才能卖出,由于10排在3的前面,这意味你要10块买进,3块卖出,你的算法给出的实际上是亏损最大化的情况。
于是你换一种思路,使用暴力枚举法,也就是对任何一种可能的买进卖出组合,例如第 i 天买入,第j 天卖出, j > i, 计算p(i, j) = S[j] – S[i], 计算所以可能的i, j 组合情况,把计算得到的最大的p(i, j) 返回。由此,你写出以下算法:
int profit = Integer.MINUM_VALUE;
for (int i = 0; i < S.length; i++)
for (int j = i + 1; j < S.length; j++) {
if (S[j] – S[i] > profit) {profit = S[j] – S[i];
}
}
接下来你要给面试官分析算法的复杂度,假定S数组的长度为 n, 那么外层循环要走n次,内层循环要走 n – i – 1 次。于是算得的总次数为:
也就说,暴力枚举法得到的算法复杂度是:
接着你再分析一下空间复杂度,由于算法中只是采用了几个局部变量,因此空间复杂度是O(1). 于是此时,你便拥有了一个可以解决问题的算法。
再接下来,你需要在上面的基础上,想办法优化,一般而言,当S的长度足够大时,平方级的时间复杂度是无法接受的。你可能想到,一种算法设计模式叫分而治之。也就是,把S 先分成两部分, 第一部分是S 的前半部:
另一部分是S的后半部:
然后,分别在前半部和后半部分别计算交易的最大利润,接着选出两个结果中的利润最大值。例如:
S:1 , 2, 3, 4, 5, 6, 7, 9
那么前半部是:1, 2, 3, 4 最佳交易方案是第一天买入,第4天卖出,得到的利润是: 3(4 – 1).
后半部是: 5, 6, 7 ,9. 最佳交易是第五天买入,第八天卖出,利润是:4(9-5).
因此采用后半部的交易方案是当前选择。
然而,我们还需要考虑一种跨界情况,最大利润可能实现的方案是,在前半部的某一天买入,在后半部的某一天卖出,如果是这种情况,那么只可能是在前半部的最小值处买入,在后半部的最大值处卖出。也就是,第一天买入,最后一天卖出,利润是 8(9-1)。
因此,我们需要在前半部找到最小值,在后半部找到最大值,一个循环就可以实现,一个循环的时间复杂度是 O(n), 这样,算法的总体复杂度是:
计算出 T(n) 为 O(n log(n)).
通过分而治之的算法,我们将效率提高了很多。只是它的实现还需要考虑不少边界条件,例如数组是空数组,数组只有一个元素,数组中的元素以降序排列等等。在你编码技能熟练的情况下,把算法写出来一般也就需要20到30分钟。
如果你能想到分而治之的方案,很可能你能通过面试,但再想想,还有没有可能再改进一下呢?上面提到的跨界情况或许能给你提示:
假定最佳交易方案是第 N 天卖出,那么很显然,买入时机是在前N-1天价格最低的时候,也就是在S[0, N-1] 最小值那时买入,把S[0, N-1]最小值记为:Min(S[0, N-1]),
那么,最大利润的值就是 profit = S[N] - Min(S[0, N-1]), 将N从1 到 n 走一便,使得profit最大化的那个值就是利润最大值。这个遍历将数组循环一次就够了, 于是我们得到一个更好的算法,其时间复杂度是O(n),该算法的实现我会在稍后的代码演示中给出。用于算法不需要额外的存储空间,仅需要数组本身加上一些变量,因此它的空间复杂度是O(1).
从上面的解题流程,我们可以看到,一次面试,大概45到60分钟,你需要根据给定问题,分析问题,设计算法,然后编码实现,接着测试代码,分析复杂度。总结来说,在成功的面试中,你必须展现一下几方面的特质:
1. 将现实世界的实际问题就行抽象归纳的能力。
2. 在较短时间内进行算法设计的能力。
3. 较强的编码能力,能将算法实现为可运行的代码
4. 对算法进行复杂度分析的能力。
大家或许可以体会到,在不到一个小时的时间内,要展现上面几种能力是比较困难的,很多情况下,你会卡在第二部,也就是算法设计,在较大的压力情况下,保持头脑清醒,并进行快速的思考分析,对大多数人来说,并不容易做到。因此,要想提高面试成功率,我们必须在平时就注意培养积累算法功底,注意分析能力的培养和提高。本课程不但将帮您提高算法设计与分析方面的能力,同时通过收集分析大量的面试算法题,从而为你总结归纳出面试算法题的特征,出题套路以及相应的解题方法。知己知彼,百战不殆,当对方的出手套路都已经在你的掌控和预料之下时,战胜他早已是情理之中了。
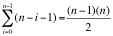
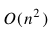
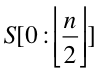
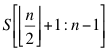
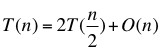


![[算法] 栈和队列](https://img-blog.csdnimg.cn/ce7df0be33f0470fb7d74a4b449cb342.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA6KW_56eR6IOh5YWI55Sf,size_20,color_FFFFFF,t_70,g_se,x_16)