目录

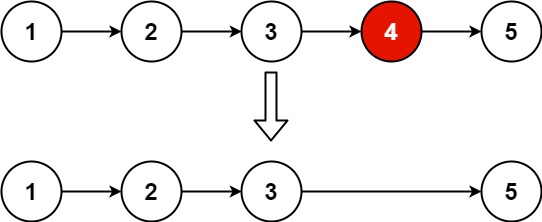
什么是剪枝

几种常见的剪枝

1.可行性剪枝

2.排除等效冗余

3.最优性剪枝

4.顺序剪枝

5.记忆化

运用实例

1.选数

2.吃奶酪

3.小木棍

---

什么是剪枝

剪枝：通过某种判断，避免一些不必要的遍历过程。搜索的时间复杂度通常很大，通过剪枝对搜索进行优化，可以大大提高程序运行的效率。

几种常见的剪枝

1.可行性剪枝

判断继续搜索是否能得到答案，如果不能，就返回

即：不可行，就返回

2.排除等效冗余

在搜索的几个分支中具有完全相同的效果时，选择其中一个走即可

即：有相同，选一个

3.最优性剪枝

和可行性剪枝有点相似，区别在于继续搜索可能得到答案，但一定不是最优

首先得到最优解：每搜索到一个解，和之前的解做对比，得到最优解

然后最优性剪枝：如果当前搜索到的解已经超过最优解，就返回

即：非最优，就返回

4.顺序剪枝

优化搜索顺序，更快得到解

即：先排序，再搜索

5.记忆化

记录每个状态的搜索结果，在后续搜索过程中检索这个状态，如果重复，就返回

即：有重复，就返回

运用实例

1.选数

（详见洛谷P1036）：从n个整数中选k个整数相加，求和为素数共有多少种

输入：n，k，n个整数

输出：种类数

运用：可行性剪枝

#include<iostream>
#include<algorithm>
#include<cmath>
#define maxn 25
using namespace std;int a[maxn];
int ans = 0;
int n, k;bool isprime(int m)
{for (int i = 2; i <= sqrt(m); i++)if (m % i == 0) return false;return true;
}void dfs(int start,int count,int sum)//当前第start个数，当前已选数个数，当前已选数和
{if(count+n-start+1<k)//（可行性剪枝）当前已选数个数+剩余数个数<要选的总数个数k{return;}if (count == k){if(isprime(sum))ans++;return;//可行性剪枝}for(int i=start;i<=n;i++){dfs(i + 1, count + 1, sum + a[i]);}
}int main()
{cin >> n >> k;for (int i = 1; i <= n; i++){cin >> a[i];}dfs(1,0,0);cout << ans;
}

2.吃奶酪

（详见洛谷P1433）：有n块奶酪，现在要把它们都吃掉，求最短的经过的距离(初始在原点处)

输入：奶酪数量n，每块奶酪的坐标

输出：最少距离（保留两位小数）

运用：可行性剪枝，最优性剪枝，记忆化剪枝

首先只加上可行性剪枝：

#include<iostream>
#include<algorithm>
#include<cmath>
#include<iomanip>
#define maxn 20
using namespace std;double ans= 0x3f3f3f3f;
int n,visited[maxn];struct POINT{double x, y;
}a[maxn];double dis(POINT& a, POINT& b)
{return sqrt(pow((a.x - b.x), 2)*1.0 + pow((a.y - b.y), 2)*1.0);
}void dfs(int now,int count,double sum)//序号,吃掉数量,距离
{   if (count == n){ans = min(ans, sum);return;//不可行，返回}for (int i = 1; i <= n; i++){if (!visited[i]){visited[i] = 1;dfs(i, count+1, sum +dis(a[now],a[i]));visited[i] = 0;}}
}int main()
{cin >> n;for (int i = 1; i <= n; i++)cin >> a[i].x >> a[i].y;a[0].x = 0;a[0].y = 0;dfs(0,0,0);cout <<fixed<<setprecision(2) << ans;
}

只能得到50分

现在加上最优性剪枝：

#include<iostream>
#include<algorithm>
#include<cmath>
#include<iomanip>
#define maxn 20
using namespace std;double ans= 0x3f3f3f3f;
int n,visited[maxn];struct POINT{double x, y;
}a[maxn];double dis(POINT& a, POINT& b)
{return sqrt(pow((a.x - b.x), 2)*1.0 + pow((a.y - b.y), 2)*1.0);
}void dfs(int now,int count,double sum)//序号,吃掉数量,距离
{if (sum >= ans)//最优性剪枝return;if (count == n){ans = min(ans, sum);return;}for (int i = 1; i <= n; i++){if (!visited[i]){visited[i] = 1;dfs(i, count+1, sum +dis(a[now],a[i]));visited[i] = 0;}}
}int main()
{cin >> n;for (int i = 1; i <= n; i++)cin >> a[i].x >> a[i].y;a[0].x = 0;a[0].y = 0;dfs(0,0,0);cout <<fixed<<setprecision(2) << ans;
}

 什么？竟然还不能通过

那就再加上记忆化剪枝，把每次计算的两点间距离都保存起来，下次遇到直接调用

#include<iostream>
#include<algorithm>
#include<cmath>
#include<iomanip>
#define maxn 20
using namespace std;double ans= 0x3f3f3f3f;
int n,visited[maxn];
double map[maxn][maxn];struct POINT{double x, y;
}a[maxn];double dis(POINT& a, POINT& b)
{return sqrt(pow((a.x - b.x), 2)*1.0 + pow((a.y - b.y), 2)*1.0);
}void dfs(int now,int count,double sum)//序号,吃掉数量,距离
{if (sum >= ans)//最优性剪枝return;if (count == n){ans = min(ans, sum);return;}for (int i = 1; i <= n; i++){if (!visited[i]){if (map[now][i])//记忆化，提取之前记录过的距离{visited[i] = 1;dfs(i, count + 1, sum + map[now][i]);visited[i] = 0;}else{map[now][i] = dis(a[now], a[i]);//记忆visited[i] = 1;dfs(i, count+1, sum +map[now][i]);visited[i] = 0;}}}
}int main()
{cin >> n;for (int i = 1; i <= n; i++)cin >> a[i].x >> a[i].y;a[0].x = 0;a[0].y = 0;dfs(0,0,0);cout <<fixed<<setprecision(2) << ans;
}

 恭喜，看来这道题不用dp是通过不了了的，然而我还不会dp，等以后再来解决吧

3.小木棍

（详见洛谷P1120）：有一些同样长的木棍被随意砍成几段，求原始木棍的最小可能长度

输入：分段后的小木棍个数n，每个小木棍的长度

输出：最小可能的长度

运用：可行性剪枝，最优性剪枝，顺序剪枝

#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;int n;
int a[110];int maxm = 0, minm = 51;//小木棍最长长度，最短长度
int ans;//当前成功拼接的木棍数
int p = 0;//木棍总长度void dfs(int x, int y, int z)//x:每根木棍期望长度，y：现在拼成长度，z：上一次使用的木棍长度
{if (ans * x == p){cout << x;exit(0);//（最优性剪枝）}for (int i = z; i >= minm; i--)//从最长的小木棍开始拼（顺序剪枝）{if (a[i] && y + i <= x)//长度为a[i]的木棍拼接起来不会超过期望长度{y += i;a[i]--;if (y == x)ans++, y = 0;//拼接成功if (y == 0)dfs(x, y, maxm);//搜索下一个木棍elsedfs(x, y, i);//搜索下一个小木棍//回溯a[i]++;if (ans > 0 && y == 0)y = x - i,ans--;else y -= i;if (y == 0) break;//拼接没有成功，返回（可行性剪枝）if (y + i == x)break;//到达上一根木棍拼接状态，返回}}
}int main()
{cin >> n;for (int i = 1; i <= n; i++){int temp;cin >> temp;if (temp <= 50){	a[temp]++;//长度为temp的木棍数量+1p += temp;maxm = max(temp, maxm);minm = min(temp, minm);}}for (int i = maxm; i <= p / 2; i++)//小木棍木棍最长长度->总长度的一半{//木棍总长度也就是原始木棍长度一定能够整除单个木棍长度if(p%i==0){ ans = 0;dfs(i, 0, maxm);//期望长度=i,现在拼成长度=0,使用长度=maxm}}cout << p;//搜索不成功，全部拼成1根}