-
基本思想
快速排序是一种采用分治法解决问题的一个典型应用,也是冒泡排序的一种改进。它的基本思想是,通过一轮排序将待排记录分割成独立的两部分,其中一部分均比另一部分小,则可分别对这两部分继续进行排序,已达到整个序列有序。排序的时间复杂度为 O(nlogn),相比于简单排序算法,运算效率大大提高。
-
算法步骤
-
从序列中取出一个数作为中轴数;
-
将比这个数大的数放到它的右边,小于或等于他的数放到它的左边;
-
再对左右区间重复第二步,直到各区间只有一个数。
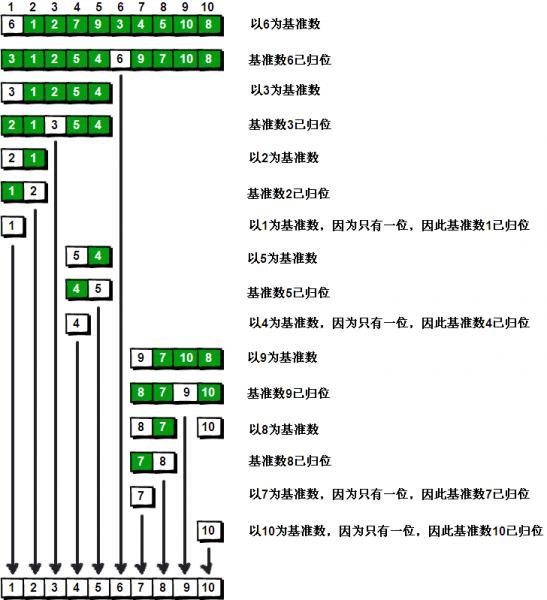
例如,对以下 10 个数进行快速排序:
6 1 2 7 9 3 4 5 10 8以第一个数为基准数,在初始状态下,数字 6 在序列的第 1 位,我们的目标是将 6 挪到序列中间的某个位置,假设这个位置是 k 。
现在就需要寻找这个 k ,并且以第 k 位为分界点,左边的数都≤6,右边的数都≥6。那么如何找到这个位置 k 呢?
我们要知道,快速排序其实是冒泡排序的一种改进,冒泡排序每次对相邻的两个数进行比较,这显然是一种比较浪费时间的。
而快速排序是分别从两端开始”探测”的,先从右往左找一个小于 6 的数,再从左往右找一个大于 6 的数,然后交换他们。这里可以用两个变量 i 和 j ,分别指向序列最左边和最右边。
我们为这两个变量起个好听的名字哨兵 i 和哨兵 j。
-
我们首先让哨兵 i 指向序列的最左边,指向数字 6;让哨兵 j 指向序列的最右边,指向数字 8,如下图所示。

-
2.首先哨兵 j 开始出动。因为此处设置的基准数是最左边的数,所以需要让哨兵 j 先出动,这一点非常重要。
- 哨兵 j 一步一步地向左挪动,直到找到一个小于 6 的数停下来
- 然后哨兵 i 再一步一步向右挪动,直到找到一个数大于 6 的数停下来
3.最后哨兵 j 停在了数字 5 面前,哨兵 i 停在了数字 7 面前,如下图所示:

4.现在交换哨兵 i 和哨兵 j 所指向元素的值,交换之后的序列如下:

5.到此,第一次交换结束。接下来开始哨兵 j 继续向左挪动(再友情提醒,每次必须是哨兵 j 先出发)。他发现了 4<6,停下来。哨兵 i 也继续向右挪动的,他发现了 9>6,停下来。此时再次进行交换,交换之后的序列如下

6.第二次交换结束。哨兵 j 继续向左挪动,他发现了 3<6,又停下来。
7.哨兵 i 继续向右移动,此时哨兵 i 和哨兵 j 相遇了,哨兵 i 和哨兵 j 都走到 3 面前。
说明此时“探测”结束。我们将基准数 6 和 3 进行交换。交换之后的序列如下。

到此第一轮“探测”真正结束。
现在基准数 6 已经归位,此时以基准数 6 为分界点,6 左边的数都小于等于 6,6 右边的数都大于等于 6。
现在我们将第一轮“探测”结束后的序列,以 6 为分界点拆分成两个序列,左边的序列是“3 1 2 5 4”,右边的序列是“9 7 10 8”。接下来还需要分别处理这两个序列,因为 6 左边和右边的序列目前都还是混乱的。不过不要紧,我们已经掌握了方法,接下来只要模拟刚才的方法分别处理 6 左边和右边的序列即可。
实际上快速排序的每一轮处理其实就是将这一轮的基准数归为,直到所有的数都归为为止,排序就结束了。
实现代码
package Sort;public class 快速排序 {public static void main(String[] args) {int[] arr = {6,1,2,7,9,3,4,5,10,8};sort(arr, 0, arr.length-1);print(arr); }public static void sort(int[] arr,int leftBound,int rightBound) {if(leftBound >= rightBound) return;int mid= partition(arr, leftBound, rightBound); //得到轴的位置sort(arr, leftBound, mid-1); //左边排序sort(arr, mid+1, rightBound); //右边排序}static int partition(int[] arr, int leftBound,int rightBound) {int pivot = arr[rightBound]; //指定数组最右边的数是用来比较的值 轴int left = leftBound;int right = rightBound - 1;while (left <= right) {while(left <= right && arr[left] <= pivot) left++;while(left <= right && arr[right] > pivot) right--;if (left < right) {//如果 左边的数比右边的数小 两个数交换swap(arr, left, right);}}//把left最后一次指向的位置与pivot(轴)的位置交换swap(arr, left, rightBound);return left; //返回轴的位置}static void swap(int[] arr,int i,int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}static void print(int[] arr) {for (int i = 0; i < arr.length; i++) {System.out.print(arr[i] + " ");}}
}