1.什么是最小生成树
来看百度百科的定义
一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n个结点,并且有保持图连通的最少的边。最小生成树可以用kruskal(克鲁斯卡尔)算法或prim(普里姆)算法求出。
意思简单明了就是求最小的连通图
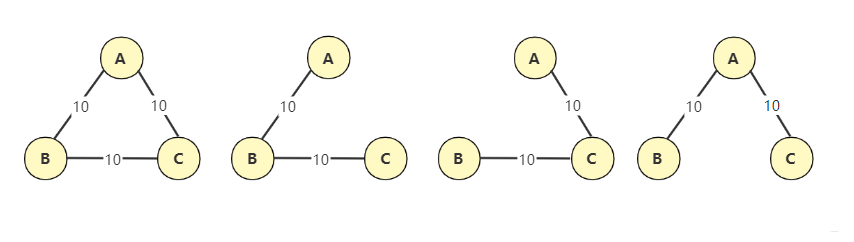
举个栗子

这幅图的极小连通图为

或者

就是从一个点能到达图的任意一点,且花费的代价最小(所有边的权值最小)
2.普里姆(Prim)算法
此算法可以称为“加点法”,每次迭代选择代价最小的边对应的点,加入到最小生成树中。算法从某一个顶点s开始,逐渐长大覆盖整个连通网的所有顶点。
从点v1开始选择离v1最近的点,可以发现v1-v3的距离最小,所以把这条边连上
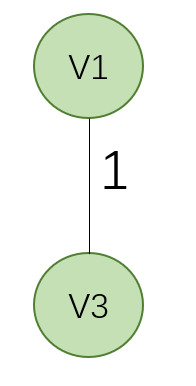
现在v1和v3作为一个整体,看那个点离v1和v3最近,此时有两个点离得最近,按顺序选择v4(也可以选择v6,是一样的)。

现在选择离v1,v3,v4最近的点,现在v4-v6这条边最短,所以选择v4-v6这条边

按照这个思路依次选择,直到把所有的点都选上


3.Prim代码
prim的核心代码为:
int prime()
{int tip = 0; //tip用来计算距离for(int i = 1 ; i <= n ; i++) // 初始化dis为无穷大dis[i] = inf;//inf = 99999999;memset(book , 0 , sizeof(book));//book用来标记点有没有被选择dis[1] = 0; //以1为结点开始for(int i = 1 ; i <= n ; i++){int k = -1 , temp = inf;for(int j = 1 ; j <= n ; j++){if(book[j] == 0 && dis[j] < temp) //在没有遍历过的顶点中找距离树最近的点{k = j;temp = dis[j];}}if(k == -1) return -1; // 有没有联通的点输出-1tip += dis[k];//记录距离book[k] = 1; //把已经收入树的顶点标记for(int j = 1 ; j <= n ; j++) //遍历该顶点与未遍历顶点的距离 更新dis{if(book[j] == 0 && f[k][j] != inf && f[k][j] < dis[j])dis[j] = f[k][j];}}return tip;
}4.克鲁斯卡(Kruskal)算法
并查集+贪心
算法思路:
(1)将图中的所有边都去掉。
(2)将边按权值从小到大的顺序添加到图中,保证添加的过程中不会形成环
(3)重复上一步直到连接所有顶点,此时就生成了最小生成树。
对所有的边进行排序

加入步骤如图

5.Kruskal算法代码:
#include<iostream>
#include<string>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
int n , m;
int f[1005];
void init() //初始化
{for(int i = 1 ; i <= n ; i++)f[i] = i;
}
struct book //用来存储边
{int k1 , k2;//顶点int dis;//权值
}e[3005];
int getf(int v) //并查集 找“领导”的函数
{if(f[v] == v)return v;else{f[v] = getf(f[v]);return f[v];}
}
bool merge1(int x , int y) //合并顶点的函数
{int t1 , t2;t1 = getf(f[x]);t2 = getf(f[y]);if(t1 != t2) //判断顶点是否在一颗树里{ f[t2] = t1;return true;}elsereturn false;
}
bool cmp(book x , book y) //结构体排序
{return x.dis < y.dis;
}
int main()
{cin>>n>>m;init();for(int i = 1 ; i <= m ; i++)cin>>e[i].k1>>e[i].k2>>e[i].dis;sort(e+1 , e+m+1 , cmp);int ans = 0; //记录最终的权值int tip = n; //用了几条边for(int i = 1 ; i <= m ; i++){if(merge1(e[i].k1 , e[i].k2)){ans += e[i].dis;tip--;if(tip == 1)break;}}if(tip == 1)cout<<ans;elsecout<<"-1";
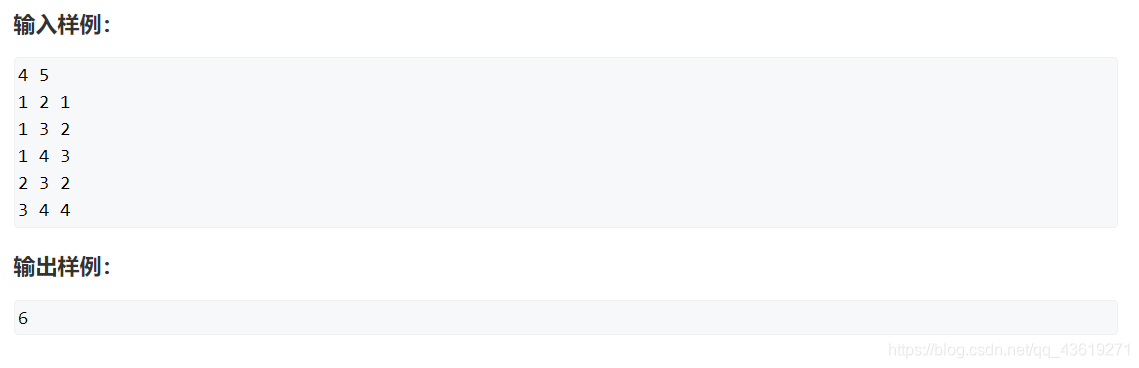
}引用的具体题目为
题目链接: 公路村村通