数位dp。。。

（建议认真学的人最好别看我的博客）
https://blog.csdn.net/KonnyWen/article/details/104475276别人的一篇博客，明天早上学！
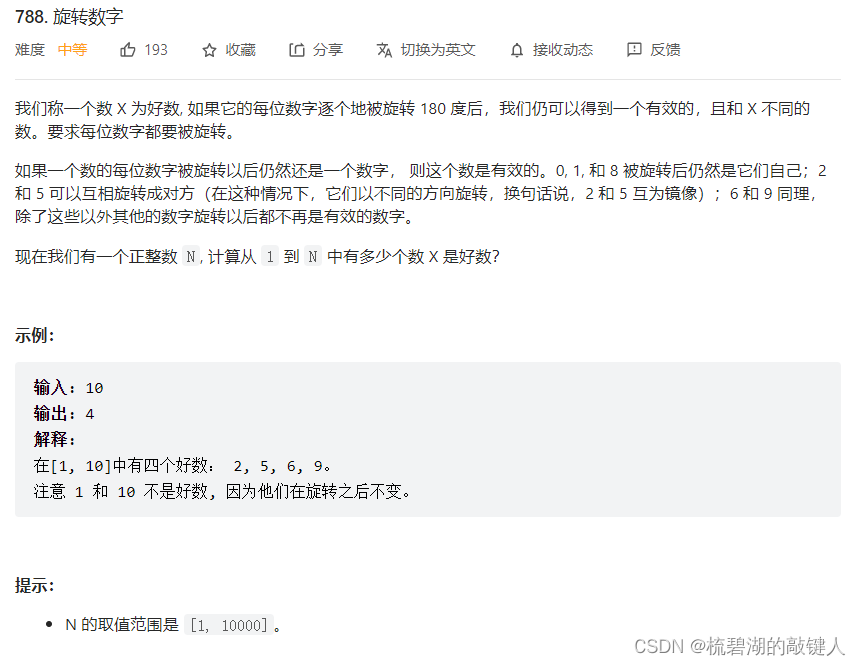
好的我们开始：数位 dp 是指求在数位限制下有多少满足要求的数的 dp \texttt{dp}dp。例如，求“在 [ L , R ] 范围内连续出现过 3 个 3 的数”，“相邻两位之间差为质数的 5 位数”或“在 [ L , R ] 区间内 6 出现的次数”。通常来说会有两种的：递推以及记忆化搜索。
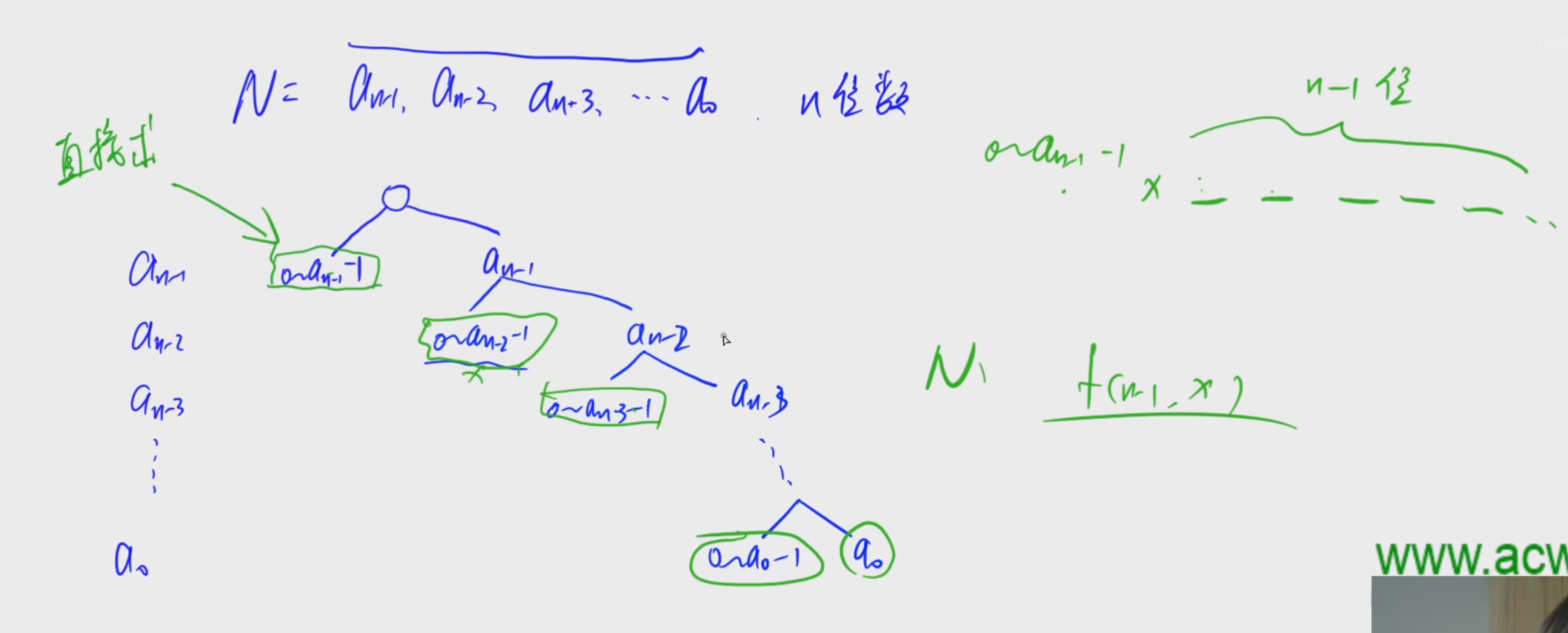
P2602 [ZJOI2010] 数字计数我们选择使用递推，可以用sum[i]表示到i位的时候，1~9的每一个数量之和，仔细想想因为只限定了位数没限定大小，那么其实1 ~ 9的数量都是相等的，0我们稍后考虑算。那么如何从前一位推上来呢，那么其实就是sum[ i ] = sum[ i-1 ]*10+10^(i-1)，(i>=2)然后sum[1] 初定为1，那么就可以处理出sum，搞定预处理之后，那么我们考虑[1,n]的出现次数。我们先用一个数组记录下n每一位的数字！然后从最高位往前做，对于一个ABCD这样的数字，分三种情况讨论A的贡献：
1.目前枚举到的数字j<A ，那么其实就相当于前面的所有和都能和上面一样转移上来；
2.目前枚举到的数字j==A，那么只能转移一部分，也就是BCD+1这一部分；
3.那么超过A的部分其实是不用算的。
然后每次往前推进一格，一直推到最低位
其实这样考虑是不完全的，我们应该考虑目前这一位，会对前面每一个数重新造成一次影响，就像已经计算过了一次123，欸~我们有1123，2123，所以要重新计算一次前面的数，但只能计算num[i]次，然后考虑前面的数对这一位能造成的贡献，那么就像前面讨论说的那样分三种。
然后考虑0，那么0其实就是所有情况减去前导0，那么怎么算呢考虑一下，若是在第三位然后前导0的数量就是0~99的数量便是10^(i-1)。在这里插入图片描述别人的博客看吧看吧。

#include<bits/stdc++.h>
#define int long long 
using namespace std;
int n,m,cnt[101],ten[101];//cnt是1~9在每一位的计数 
void init()
{ten[0]=1;for(int i=1;i<=12;i++){ten[i]=ten[i-1]*10;//预处理10^i cnt[i]=cnt[i-1]*10+ten[i-1];//预处理每一位的值，注意不是前缀和哈，是本身的贡献 }return ;
}
int num[10001];
void make(int x,int f[])
{int k=x,len=0;while(x) num[++len]=x%10,x/=10;for(int i=len;i>=1;i--){for(int j=0;j<=9;j++) f[j]+=cnt[i-1]*num[i];//对前面每一位都会造成贡献 for(int j=0;j<=num[i]-1;j++) f[j]+=ten[i-1];//前面i-1为对i位为j时的贡献 k-=num[i]*ten[i-1];f[num[i]]+=k+1;//算上num[i]0000的情况f[0]-=ten[i-1]; }return ;
}	
int f1[11],f2[11];
signed main()
{int a,b;scanf("%lld%lld",&a,&b);init();make(a-1,f1);make(b,f2);for(int i=0;i<=9;i++) printf("%lld ",f2[i]-f1[i]); return 0;
}

然后做一道寄搜，P2657 [SCOI2009] windy 数，我抄的那个还是麻烦了，他选择的是先用递推算除最高位的所有答案，然后再从最高位开始找起。在这里插入图片描述

#include<bits/stdc++.h> 
#define int long long  
using namespace std;
int n,m,f[18][18],g[18][18],num[18];
void init()
{for(int i=0;i<=9;i++) f[1][i]=1;for(int i=2;i<=10;i++){for(int j=0;j<=9;j++){for(int J=0;J<=9;J++) {if(abs(j-J)>=2) f[i][j]+=f[i-1][J];}	} } return ;
}
int dfs(int w,int d,bool free)
{if(!w) return 1;if(free&&~g[w][d]) return g[w][d];int up=free?9:num[w],rt=0;for(int i=0;i<=up;i++) {if(abs(i-d)>=2) rt+=dfs(w-1,i,free||i<up);}if(free) g[w][d]=rt;return rt;
} 
int dp(int x)
{int len=0,ans=0;memset(g,-1,sizeof(g));while(x) num[++len]=x%10,x/=10;for(int i=1;i<=num[len];i++) ans+=dfs(len-1,i,i<num[len]);for(int i=len-1;i>=1;i--){for(int j=1;j<=9;j++) ans+=f[i][j];//printf("%lld\n",ans);}return ans;
}
main()
{int a,b;scanf("%lld%lld",&a,&b);init();printf("%lld\n",dp(b)-dp(a-1));return 0;
}

决定重新打一个板子：

#include<bits/stdc++.h>
#define int long long 
using namespace std;
int n,m,f[1001][11],num[100001];//我们用f[i,j]表示搜到i，当前的值(i-1)值是j
int dfs(int len,int x,bool free,bool zer)
{if(!len) return 1;if(!free&&!zer&&f[len][x]!=-1) return f[len][x];int up=9,rt=0;if(free) up=num[len];for(int i=0;i<=up;i++){if(abs(x-i)<2&&!zer) continue ;if(zer&&i==0) rt+=dfs(len-1,i,i==up&&free,true);else rt+=dfs(len-1,i,i==up&&free,false);}if(!free&&!zer) f[len][x]=rt;return rt;
}
int dp(int x)
{int len=0;memset(f,-1,sizeof(f));while(x) num[++len]=x%10,x/=10;return dfs(len,0,true,true);
}
main()
{int a,b;scanf("%lld%lld",&a,&b);printf("%lld",dp(b)-dp(a-1));return 0;
}

欸P4999 烦人的数学作业这一题！是一个比较简单的数位dp，我决定摆烂。

#include<bits/stdc++.h>
#define int long long 
using namespace std;
int n,m,mod=1e9+7,cnt[100],ten[101];
void init()
{ten[0]=1;for(int i=1;i<=20;i++) {ten[i]=(ten[i-1]*10)%mod;cnt[i]=(cnt[i-1]*10+ten[i-1])%mod;}return ;
}
int num[100];
void make(int x,int f[])
{int k=x,len=0;while(x) num[++len]=x%10,x/=10;//printf("<<%lld",len); for(int i=len;i>=1;i--){for(int j=0;j<=9;j++) f[j]=(f[j]+cnt[i-1]*num[i])%mod;for(int j=0;j<=num[i]-1;j++) f[j]=(f[j]+ten[i-1])%mod;k-=num[i]*ten[i-1];f[num[i]]=(f[num[i]]+k+1)%mod;}return ;
}
int f1[100],f2[100];
signed main()
{int t;scanf("%lld",&t);init();while(t--){int a,b,ans=0;scanf("%lld%lld",&a,&b);memset(f1,0,sizeof(f1));make(a-1,f1);memset(f2,0,sizeof(f2));make(b,f2);for(int i=0;i<=9;i++) ans=(ans+(f2[i]-f1[i])*i%mod+mod)%mod;printf("%lld\n",ans);}return 0;
}

P6218 [USACO06NOV] Round Numbers S
相对而言，我认为寄搜的方式会更好理解些。那么你需要注意的地方是，前导0以及是否为最大值，若是的话就要单独计算，若不是，那就直接继承之前的值。

#include<bits/stdc++.h>
#define int long long 
using namespace std;
int n,m,f[101][110][101];//剩下a位，b个1，c个0 （其实可以化简） 
int num[100001],mod=1e7+7;
int dfs(int len,int sum0,int sum1,bool free,bool zero)//free指的是前一位能否取到最大值，zero指的是是否有前导0 
{if(len==0){//printf("%lld %lld %lld\n",len,sum0,sum1);if(sum1<=sum0) return 1;else return 0;}if(!free&&!zero&&f[len][sum0][sum1]!=-1) return f[len][sum0][sum1];int up=1,rt=0;if(free) up=num[len];for(int i=0;i<=up;i++){if(zero&&i==0) rt+=dfs(len-1,0,0,free && i==up,true);else rt+=dfs(len-1,sum0+(i==0),sum1+(i==1),free && i==up,false);}if(!free&&!zero) f[len][sum0][sum1]=rt;return rt; 
}
int dp(int x)
{int len=0;memset(f,-1,sizeof(f));	 while(x) num[++len]=x&1,x>>=1;//printf("%lld\n",len);return dfs(len,0,0,true,true);
}
main()
{int a,b;scanf("%lld%lld",&a,&b);printf("%lld",dp(b)-dp(a-1));return 0;
}

好像，我大概也懂了些寄搜罢P1836 数页码

#include<bits/stdc++.h>
#define int long long 
using namespace std;
int n,m,num[10001],f[12][10001];
int dfs(int len,int sum,bool free,bool zer)
{if(len==0) return sum;if(!free&&!zer&&f[len][sum]!=-1) return f[len][sum];int up=9,rt=0;if(free) up=num[len];for(int i=0;i<=up;i++) rt+=dfs(len-1,sum+i,free&(i==up),zer	&(i==0));if(!free&&!zer) f[len][sum]=rt;return rt;
}
int dp(int x)
{int len=0;memset(f,-1,sizeof(f));	while(x) num[++len]=x%10,x/=10;return dfs(len,0,true,true);
}
main()
{int x;scanf("%lld",&x);printf("%lld",dp(x));return 0;	
}

P4317 花神的数论题这个tm裸的但是模的很阴间然后数组要开50你敢信。

#include<bits/stdc++.h>
#define int long long 
using namespace std;
int n,m,num[1000001],f[50][100001],mod=10000007;
int dfs(int len,int x,bool free,bool zer)
{if(!len) return max(x,1ll);if(!free&&!zer&&f[len][x]!=-1) return f[len][x]%mod;int up=1,rt=1;if(free) up=num[len];for(int i=0;i<=up;i++) rt=(rt*dfs(len-1,x+i,free&i==up,zer&&i==0))%mod;if(!free&&!zer) f[len][x]=rt;return rt;
}
int dp(int x)
{int len=0;memset(f,-1,sizeof(f));while(x) num[++len]=x&1,x>>=1;return dfs(len,0,true,true);
}
signed main()
{int x;scanf("%lld",&x);printf("%lld",dp(x));return 0;
}

其实做了这么多题，都只是为了补一题：Digit Sum草走忽略，这东西有东西的，不干净，我不知道调了半天都不知道为什么错。

#include<bits/stdc++.h>
#define int long long 
using namespace std;
int n,m,k,num[20001],f[20001][1000],mod=1e9+7;
int dfs(int len,int x,bool free,bool zer)
{if(len==0) return (x%k==0);if(!free&&!zer&&f[len][x%k]!=-1) return f[len][x%k];int up=9,rt=0;if(free) up=num[len];for(int i=0;i<=up;i++) rt=(rt+dfs(len-1,(x+i)%k,free & (i==up),zer & (i==0)))%mod;if(!free&&!zer) f[len][x%k]=rt%mod;return rt%mod;
}
int dp(char x[])
{int len=strlen(x+1);memset(f,-1,sizeof(f));for(int i=1;i<=len;i++) num[len-i+1]=x[i]-'0';return dfs(len,0,true,true);
}
signed main()
{char x[100001];scanf("%s%lld",x+1,&k);int ans=dp(x)%mod;
//	if(ans==0) printf("0");
//	else printf("%lld",(ans-1+mod)%mod);return 0;
}

Classy Numbers

#include<bits/stdc++.h>
#define int long long 
using namespace std;
int n,m,num[101],f[100][1001];
int dfs(int len,int st,bool free,bool zer)
{if(st>3) return 0;if(len==0) return 1;if(!free&&!zer&&f[len][st]!=-1) return f[len][st];int up=9,rt=0;if(free) up=num[len];for(int i=0;i<=up;i++) rt+=dfs(len-1,st+(i!=0),free & i==num[len],zer & (i==0));if(!zer&&!free) f[len][st]=rt;return rt;
}
int dp(int x)
{int len=0;memset(f,-1,sizeof(f));while(x) num[++len]=x%10,x/=10;return dfs(len,0,true,true);
}
signed main()
{int t;scanf("%lld",&t);while(t--) {int l,r;scanf("%lld%lld",&l,&r);printf("%lld\n",dp(r)-dp(l-1));}return 0;
}

然后又重温一遍板子统计问题 The Counting Problem

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,cnt[10001],ten[10001];
int num[10001],f1[10001],f2[10001];
void init()
{ten[0]=1;for(int i=1;i<=14;i++){ten[i]=ten[i-1]*10;cnt[i]=cnt[i-1]*10+ten[i-1];}return ;
}
void dp(int x,int f[])
{int len=0,k=x;while(x) num[++len]=x%10,x/=10;//printf("%lld ",len);for(int i=len;i>=1;i--){for(int j=0;j<=9;j++) f[j]+=cnt[i-1]*num[i];for(int j=0;j<=num[i]-1;j++) f[j]+=ten[i-1];k-=num[i]*ten[i-1];f[num[i]]+=k+1;f[0]-=ten[i-1];}return ;
}
main()
{int l,r;init();while(scanf("%lld%lld",&l,&r)){if(l==0&&r==0) break;if(l>r) swap(l,r);memset(f1,0,sizeof(f1));dp(l-1,f1);memset(f2,0,sizeof(f2));dp(r,f2);for(int i=0;i<=8;i++) printf("%lld ",f2[i]-f1[i]);printf("%lld\n",f2[9]-f1[9]);}return 0;	
}

dfs大法好啊~Salazar Slytherin’s Locket，欸明天就能去看她咯~，害可惜刚刚没有看到呢，不知道人去哪了。好吧刚刚uke的原因是应该开多维的数组来保存每一进制的值，所以这样就可以只初始化一次就行啦。

//观题，最多区十位之数，直接压成二进制，若是最终为0，便可输出，哦对记得0不能算在内； 
#include<bits/stdc++.h>
#define int long long 
using namespace std;
int n,m,f[12][100][2001],num[20001],b;
int dfs(int len,int x,bool free,bool zer)
{ if(len==0) return !x;if(!free&&!zer&&f[b][len][x]!=-1) return f[b][len][x];	int up=b-1,rt=0;if(free) up=num[len];for(int i=0;i<=up;i++){if(i==0&&zer) rt+=dfs(len-1,x,free & i==up,zer & i==0);else rt+=dfs(len-1,x^(1<<i),free & i==up,zer & i==0);}if(!free&&!zer) f[b][len][x]=rt;//printf("%lld\n",rt);return rt;
}
int dp(int x)
{int len=0;//memset(f,-1,sizeof(f));while(x) num[++len]=x%b,x/=b;return dfs(len,0,true,true);
}
main() 
{memset(f,-1,sizeof(f));int t;scanf("%lld",&t);while(t--){int x,y;scanf("%lld%lld%lld",&b,&x,&y);printf("%lld\n",dp(y)-dp(x-1));}return 0;
}