一,思想:
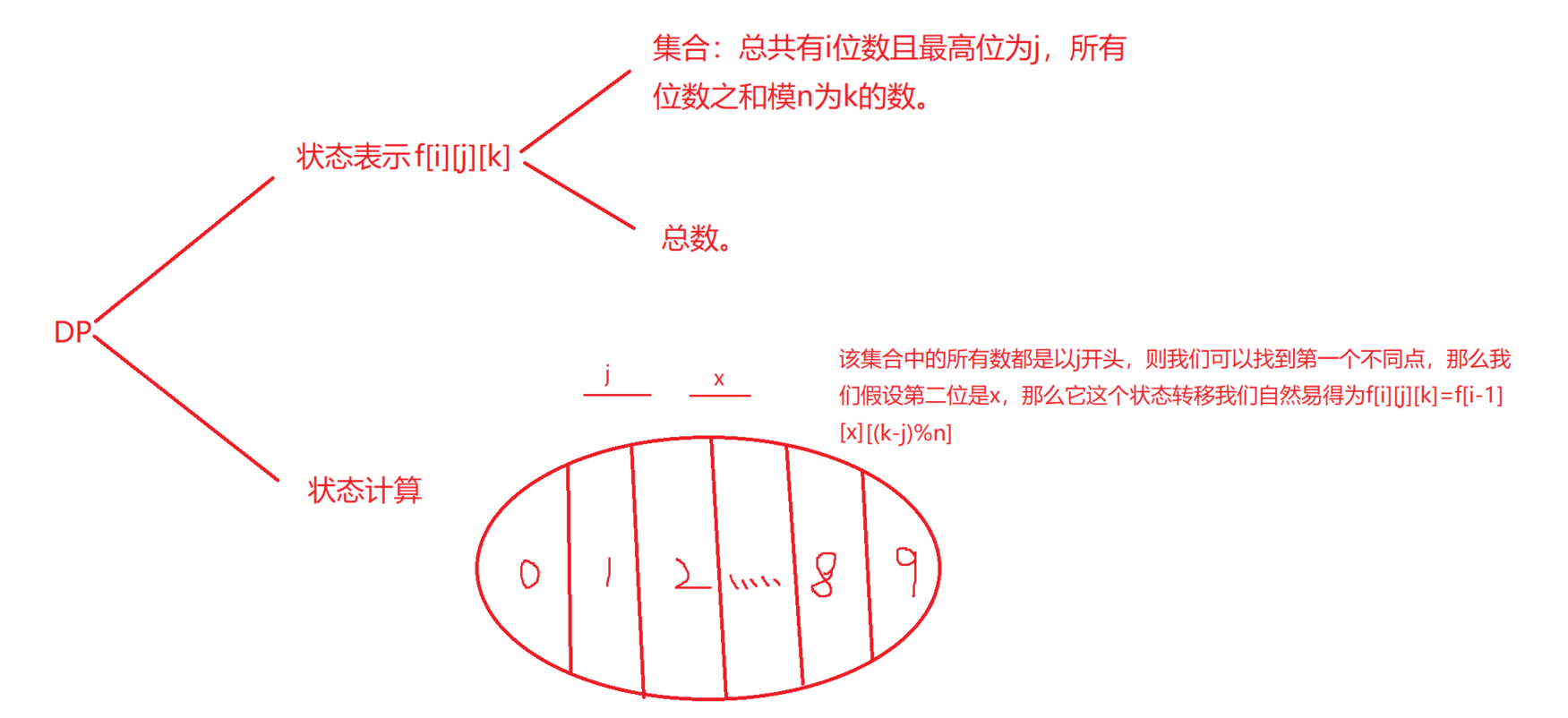
在处理1e9甚至1e18,1e100的问题时,因为在统计情况下有很多重复的计算,数位dp实现了相同状态只计算一次,从而大幅减少运算时间,思想就是对每一位进行dp,计算时记忆化每一位可以有的状态。
如我们在统计1234的状态时,可以拆成统计0~10000,0~2000,0~300,0~40数位统计
我们用bit数组由低到高存储每一位,bit[1]=4,bit[2]=3,bit[3]=2,bit[4]=1.
然后dp从高位到低位进行
const int N = 20;
int dp[20][N],bit[N];
int dfs(int len,int sta,bool limit)//limit表示当前位有没有被bit限制
{if(!len)return (sta==1);//进行到最后一位,判断状态是否符合情况,符合就+1if(!limit&&dp[len][sta]!=-1)return dp[len][sta];//如果记忆化过,直接返回int ans=0;int top=limit?bit[len]:9;//如果有限制,如1234,当前len=4,那么top<=bit[4]=1,有限制,没有limit限制就可以0~9for(int i=0; i<=top; ++i)if(状态)ans+=dfs(len-1,newsta,limit&&i==top);//累积符合状态的情况if(!limit)return dp[len][sta]=ans;//如果没有限制,即我们现在计算出来符合该状态的所有情况数(没有被限制的)那么可以记忆下来return ans;
}int cal(int x)//把数字x按位存储到数组
{int len=0;while(x)bit[++len]=x%10,x/=10;return dfs(len,0,1);
}注意事项:
- 前导0问题,在数位dp中,0,000,0000是看成不同的,所以统计答案需要考虑他们是否有影响
- 继承问题,如从高位到低位计算0000123,前面4个0是初始状态,有时继承时需要特判考虑
例题1,Problem - 4507 (hdu.edu.cn)
思路:
- 对于数位dp求取与7无关的数,操作是简单的。无脑模拟即可
- 首先显然的,我们每一位没有7
- 然后他的状态就是前面各位的累积和模7,前面的数模7。如果当前len位时,前面的累积(dsum)模7相等且前面的数字(ssum)模7也相等,可以视作同一个状态
- 但是他加了个平方限制,即有继承关系,我们可以把每个平方数看成(A+B)^2.即我们对每个len可以记录他当前位符合条件的数的平方(ssum),与当前位符合条件的数的和(dsum)。
- 假设我们当前位的数字是i,如果我们已经记录了后代的B^2与B,后代一共有cnt个符合要求的数。
- 那么更新当前位
即(A+B)^2。
,即a+b。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl "\n"
#define int long long
const int N = 21;
const int mod=1e9+7;
struct node
{int cnt,dsum,ssum;node(){cnt=-1,dsum=0,ssum=0;//记录B^2和与B和}node(int a,int b,int c):cnt(a),dsum(b),ssum(c) {};
} dp[N][N][N];
int bit[N],pre[N];node dfs(int len,int dsum,int ssum,bool limit)
{if(!len)return (dsum&&ssum?node(1,0,0):node(-1,0,0));if(!limit&&dp[len][dsum][ssum].cnt!=-1)return dp[len][dsum][ssum];node ans;int top=limit?bit[len]:9;for(int i=0; i<=top; ++i)if(i!=7){node tmp=dfs(len-1,(dsum+i)%7,(ssum*10+i)%7,limit&&i==top);if(tmp.cnt!=-1)//子代有符合情况的{if(ans.cnt==-1)ans.cnt=0;int A=i*pre[len]%mod;ans.cnt=(ans.cnt+tmp.cnt)%mod;ans.ssum=(ans.ssum+tmp.ssum+2*tmp.dsum*A%mod+tmp.cnt*A%mod*A%mod)%mod;ans.dsum=(ans.dsum+tmp.dsum+tmp.cnt*A%mod)%mod;}}if(!limit)return dp[len][dsum][ssum]=ans;return ans;
}int cal(int x)
{int k=0;while(x)bit[++k]=x%10,x/=10;return dfs(k,0,0,1).ssum;
}
void mysolve()
{int l,r;cin>>l>>r;cout<<(cal(r)-cal(l-1)+mod)%mod<<endl;
}int32_t main()
{std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);ll t=1;cin >> t;pre[1]=1;for(int i=2; i<=20; ++i)pre[i]=pre[i-1]*10%mod;//预处理10^lenwhile (t--){mysolve();}system("pause");return 0;
}例题2:Problem - 3709 (hdu.edu.cn)
思路:
- 数位只有18,而sum<=(9*19*18/2)<2000,我们可以枚举pos的每个位置来dp,如果最后sum=0,说明符合
- 如果sum<0,提前退出,不符合
- 所以他的状态是在当前枚举的是pos位,现在在len位时,累积sum的状态能获得的答案
- 需要考虑前导0,因为对于0,00,000000,哪个位置枚举pos都是一样的,重复计算len次,我们只需要1次。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl "\n"
#define int long long
const int N = 30;
int dp[N][N][2000],bit[N];int dfs(int len,int sum,int pos,bool limit)
{if(!len)return sum==0;if(sum<0)return 0;if(!limit&&dp[len][pos][sum]!=-1)return dp[len][pos][sum];int ans=0;int top=limit?bit[len]:9;for(int i=0; i<=top; ++i)ans+=dfs(len-1,sum+i*(len-pos),pos,limit&&i==top);if(!limit)return dp[len][pos][sum]=ans;return ans;
}
int cal(int x)
{if(x<0)return 1;int k=0;while(x)bit[++k]=x%10,x/=10;int ans=0;for(int i=0; i<=k; ++i)ans+=dfs(k,0,i,1);//枚举posreturn ans-k+1;//剔除多余前导0
}
void mysolve()
{int l,r;cin>>l>>r;cout<<cal(r)-cal(l-1)<<endl;
}int32_t main()
{std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);ll t=1;cin >> t;memset(dp,-1,sizeof(dp));while (t--){mysolve();}system("pause");return 0;
}例题3:Problem - 4352 (hdu.edu.cn)
思路:
- 首先,我们知道在O(n*logn)下就可以求出lis。
- 因为数位的特性,lis<=10,数字是0~9,我们可以用状压来表示他的当前状态。用数字x存储状态,如果x的二进制上i位为1,说明其lis含这个数字,我们更新时也是更新x
- 这样,数位的状态就是在求取lis为k时,当前长度为len时,其当前lic的状态为x可能的答案数。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define endl "\n"
#define int long long
const int N = 20;
int dp[N][2000][N],bit[N];
int k;
int tocnt(int x)//计数lis
{int cnt=0;for(int i=0; i<10; ++i)if(x&(1<<i))cnt++;return cnt;
}int update(int x,int p)
{for(int i=p; i<10; ++i)if(x&(1<<i))return (x^(1<<i))|(1<<p);//更新lis就是贪心从比p第一个大的数更新,表示lis为相同长度时,用p可以更小return x|(1<<p);//找不到比p大的,那么lis长度加1,即加了个p
}int dfs(int len,int x,bool limit)
{if(!len)return tocnt(x)==k;if(!limit&&dp[len][x][k]!=-1)return dp[len][x][k];int ans=0;int top=limit?bit[len]:9;for(int i=0; i<=top; ++i)ans+=dfs(len-1,(!x&&!i?0:update(x,i)),limit&&i==top);//!x&&!i?0:update(x,i)处理第一次继承问题,即前面都是0,如果当前i为0或为其他的情况if(!limit)return dp[len][x][k]=ans;return ans;
}int cal(int x)
{int len=0;while(x)bit[++len]=x%10,x/=10;return dfs(len,0,1);
}int tt=0;
void mysolve()
{int l,r;cin>>l>>r>>k;cout<<"Case #"<<++tt<<": ";cout<<cal(r)-cal(l-1)<<endl;
}int32_t main()
{std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);ll t=1;cin >> t;memset(dp,-1,sizeof(dp));while (t--){mysolve();}system("pause");return 0;
}