数位dp（模板）

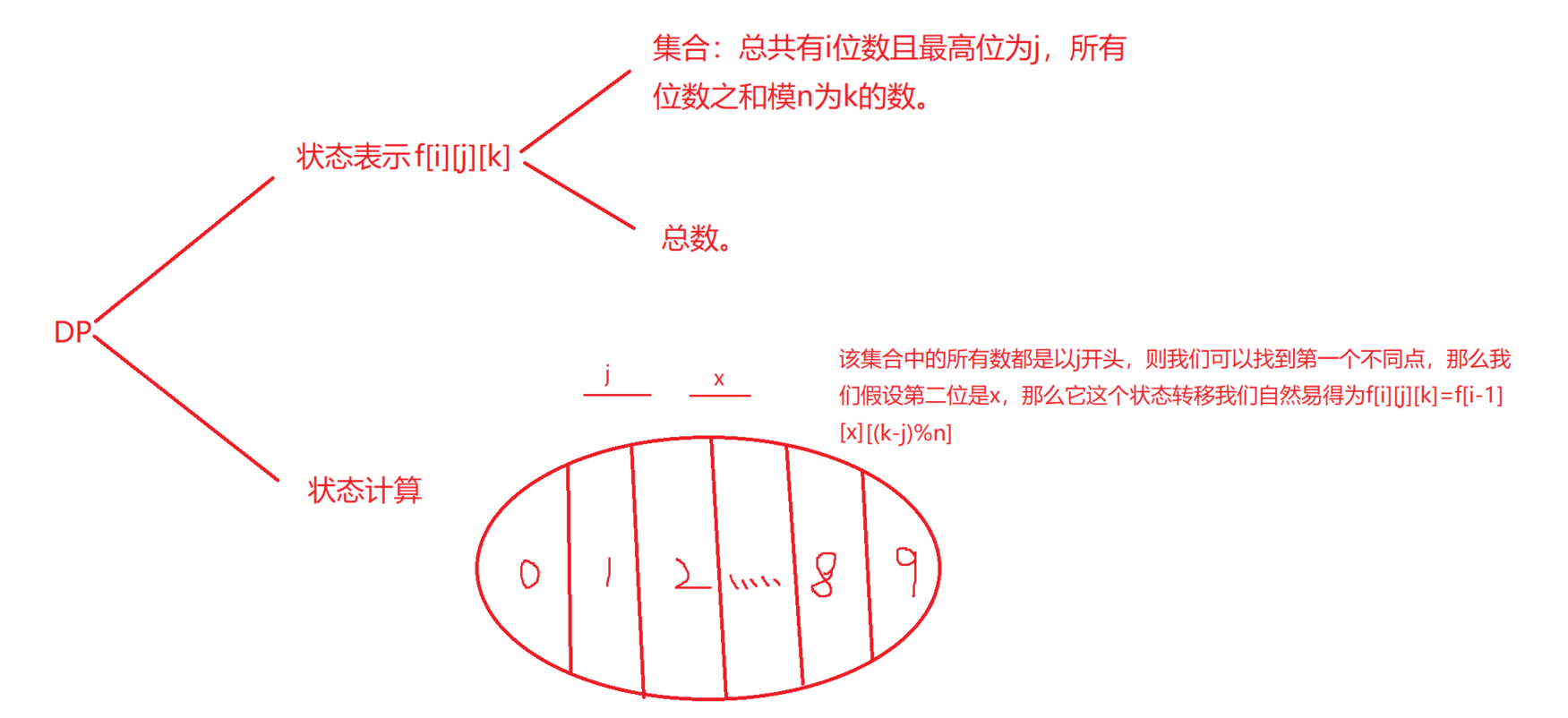
数位dp问题题型往往是这样的：

给定一个区间[L,R]，求这个区间中满足“某种条件”的数的总数。

题目：求区间[L,R]范围内有多少带3的数，所谓带3的数就是这个数十进制表示中存在至少一位3

比如3,，123,3333,都是带3的数，如12,456,1000都是不带3的数

输入:一行包含两个整数L，R（1<=L<R<1e12）

输出：输出一个整数表示区间[L,R]范围内带3的个数

例子：输入 100 2000

输出：19

在数位dp中由于数字过大，基本都要使用记忆化搜索，我们通过分析可以知道，在dfs中很多的数和前面dfs算过的数是一样的，只要不在限制位，我们把它存起来直接用就行了

#include<iostream>
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define maxn 15
int num;
int* a = new int[maxn];
int f[15];
//int a[maxn];
int b[maxn];//b保存第p为存的是那个数
int ten[maxn];
int L, R;
int t;
int dfs(int p, bool limit) {//p表示在第p位，limite表示此时是否处于限制位if (p < 0) {//for (int i = 2; i >= 0; i--)cout << b[i];//无限递归,记得加结束return//cout << endl;return 0;//搜索结束，返回}if (!limit && f[p] != -1) {//记忆化搜索，不处于限制位，并且f[p]被算过了return f[p];}int up = limit ? a[p] : 9;//判断是否处于限制位，如果是就只能取到a[p]为，否则最高位能取到9int ans = 0;for (int i = 0; i <= up; i++) {//b[p] = i;if (i == 3) {if (limit && i == up) {ans += 1;for (int j = p - 1; j >= 0; j--)//处于限制条件就把限制数下面全算上ans += a[j] * ten[j];}else//如果不处于限制条件直接加上10的p次方ans += ten[p];}else ans += dfs(p - 1, limit && i == up);//这里填a[p]可以填up也行，在处于限制的时候up等于a[p]}if (!limit)//记忆化搜索，如果没有处于限制条件就可以直接那算过一次的数直接用，能节省很多时间f[p] = ans;return ans;
}int handle(int num) {int p = 0;while (num) {//把num中的每一位放入数组a[p++] = num % 10;num /= 10;}//说明a数组写进去了，但是读取无效数据是什么意思勒，之前好像不是这样的，解决办法，动态创建数组/*for (int i = 0; i < p; i++) {cout << a[i];}*/return dfs(p - 1, true);//对应的最高位为p-1位，为True表示没有处于限制位
}void init() {ten[0] = 1;for (int i = 1; i < 15; i++) {ten[i] = ten[i - 1] * 10;}memset(f, -1, sizeof(f));
}
int32_t  main() {cin>>t;while(t--){cin>>L>>R;//handle(23);init();//一定要记得初始化，TM的我在这卡了半个月cout << handle(R)-handle(L) << endl;delete[]a;}return 0;
}

如果要输出不带3 的数只要把上面的代码的函数修改一下就好了

dfs函数修改成这样：如果是带3的数就直接continue掉，而把不带3 的数加起来

int dfs(int p, bool limit) {//p表示在第p位，limite表示此时是否处于限制位//求不带3的个数if (p < 0)return 1;//说明位数全递归了if (!limit && f[p] != -1)return f[p];//记忆化搜索，直接返回算过的值，减少计算时间int up = limit ? a[p] : 9;int ans = 0;for (int i = 0; i <= up; i++) {if (i == 3)continue;ans += dfs(p - 1, limit && i == up);}if (!limit)f[p] = ans;//记忆化搜索return ans;
}

handle函数修改：因为我们还要用到num所以num的值不能改变，要定义另外一个num来计算num的每一位数：

int handle(int num) {int p = 0;int x = num;while (x) {//把num中的每一位放入数组a[p++] = x % 10;x /= 10;}//说明a数组写进去了，但是读取无效数据是什么意思勒，之前好像不是这样的，解决办法，动态创建数组/*for (int i = 0; i < p; i++) {cout << a[i];}*/return num + 1 - dfs(p - 1, true);//对应的最高位为p-1位，为True表示没有处于限制位//在0到num中有num+1个数
}

下面就是算不带3的数的所有代码了：

#include<iostream>
using namespace std;
#define int long long
#define maxn 15
int num;
int* a = new int[maxn];
int f[15];
//int a[maxn];
int b[maxn];//b保存第p为存的是那个数
int ten[maxn];
int L, R;
int t;
int dfs(int p, bool limit) {//p表示在第p位，limite表示此时是否处于限制位//求不带3的个数if (p < 0)return 1;//说明位数全递归了if (!limit && f[p] != -1)return f[p];//记忆化搜索，直接返回算过的值，减少计算时间int up = limit ? a[p] : 9;int ans = 0;for (int i = 0; i <= up; i++) {if (i == 3)continue;ans += dfs(p - 1, limit && i == up);}if (!limit)f[p] = ans;//记忆化搜索return ans;
}int handle(int num) {int p = 0;int x = num;while (x) {//把num中的每一位放入数组a[p++] = x % 10;x /= 10;}//说明a数组写进去了，但是读取无效数据是什么意思勒，之前好像不是这样的，解决办法，动态创建数组/*for (int i = 0; i < p; i++) {cout << a[i];}*/return num + 1 - dfs(p - 1, true);//对应的最高位为p-1位，为True表示没有处于限制位//在0到num中有num+1个数
}void init() {ten[0] = 1;for (int i = 1; i < 15; i++) {ten[i] = ten[i - 1] * 10;}memset(f, -1, sizeof(f));
}
int32_t  main() {cin >> t;while (t--) {cin >> L >> R;//handle(23);init();//一定要记得初始化，TM的我在这卡了半个月cout << handle(200) - handle(100) << endl;delete[]a;}return 0;
}

杭州人称那些傻乎乎粘嗒嗒的人为62（音：laoer）。
杭州交通管理局经常会扩充一些的士车牌照，新近出来一个好消息，以后上牌照，不再含有不吉利的数字了，这样一来，就可以消除个别的士司机和乘客的心理障碍，更安全地服务大众。
不吉利的数字为所有含有4或62的号码。例如：
62315 73418 88914
都属于不吉利号码。但是，61152虽然含有6和2，但不是62连号，所以不属于不吉利数字之列。
你的任务是，对于每次给出的一个牌照区间号，推断出交管局今次又要实际上给多少辆新的士车上牌照了。

Input

输入的都是整数对n、m（0<n≤m<1000000），如果遇到都是0的整数对，则输入结束。

Output

对于每个整数对，输出一个不含有不吉利数字的统计个数，该数值占一行位置。

Sample Input

1 100
0 0

Sample Output

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
#define LL long long
using namespace std;
int digit[10];
LL dp[10][2];
LL dfs(int len, int if6, int limit)
{if (len == 0) return 1; //数到第0位返回1，因为0符合条件if (!limit && dp[len][if6]) return dp[len][if6];//如果不是上限，则不用重新数，直接返回，记忆化搜索的体现LL ans = 0, up;if (limit)  up = digit[len];else up = 9;for (int i = 0; i <= up; i++){if (if6 && i == 2) continue;if (i == 4) continue;ans += dfs(len - 1, i == 6, limit && i == digit[len]);//  limit&&i==up也可以}if (!limit) dp[len][if6] = ans;//记忆化搜索return ans;
}
LL cal(LL x)
{int len = 0;while (x){digit[++len] = x % 10;x /= 10;}return dfs(len, 0, 1);
}
int main()
{int n, m;while (~scanf("%d%d", &n, &m)){if (!n && !m)break;// printf("%lld  %lld\n",cal(m),cal(n));printf("%lld\n", cal(m) - cal(n - 1));}return 0;
}

下面这个一样是不带49的数

题目：求区间[1,n]范围内包含带49的数。

一个数是带49的数，当且仅当他的十进制标示值中存在连续的两位，其中高位为4，较低位为9，比如49,149,1234987等；而4,12345,94,9999444都不是

输入格式：输入一个整数n（1<=n<=2^63）

输出格式：输出一个整数表示区间[1,n]范围内存在多少带49的数

输出样例：

输入：500

输出：15

#include<iostream>
#include<bits/stdc++.h>
#define int long long
using namespace std;
int a[22], f[22][10];//后面这个10用于确定前面那个数是哪一个
int n;
int t;
int dfs(int p, int pre, bool limit) {//p表示第p位数，pre表示p+1位数if (p < 0) {return 1;}if (!limit && f[p][pre] != -1) {return f[p][pre];}int up = limit ? a[p] : 9;int ans = 0;for (int i = 0; i <= up; i++) {if (pre == 4 && i == 9) {continue;}ans += dfs(p - 1, i, limit && i == up);}if (!limit)f[p][pre] = ans;return ans;
}
int handle(int num) {int p = 0;int x = num;while (x) {a[p++] = x % 10;x /= 10;}return num + 1 - dfs(p - 1, 0, true);
}void init() {memset(f, -1, sizeof(f));}
int32_t main() {cin >> t;while (t--) {cin >> n;init();cout << handle(n) << endl;}return 0;
}