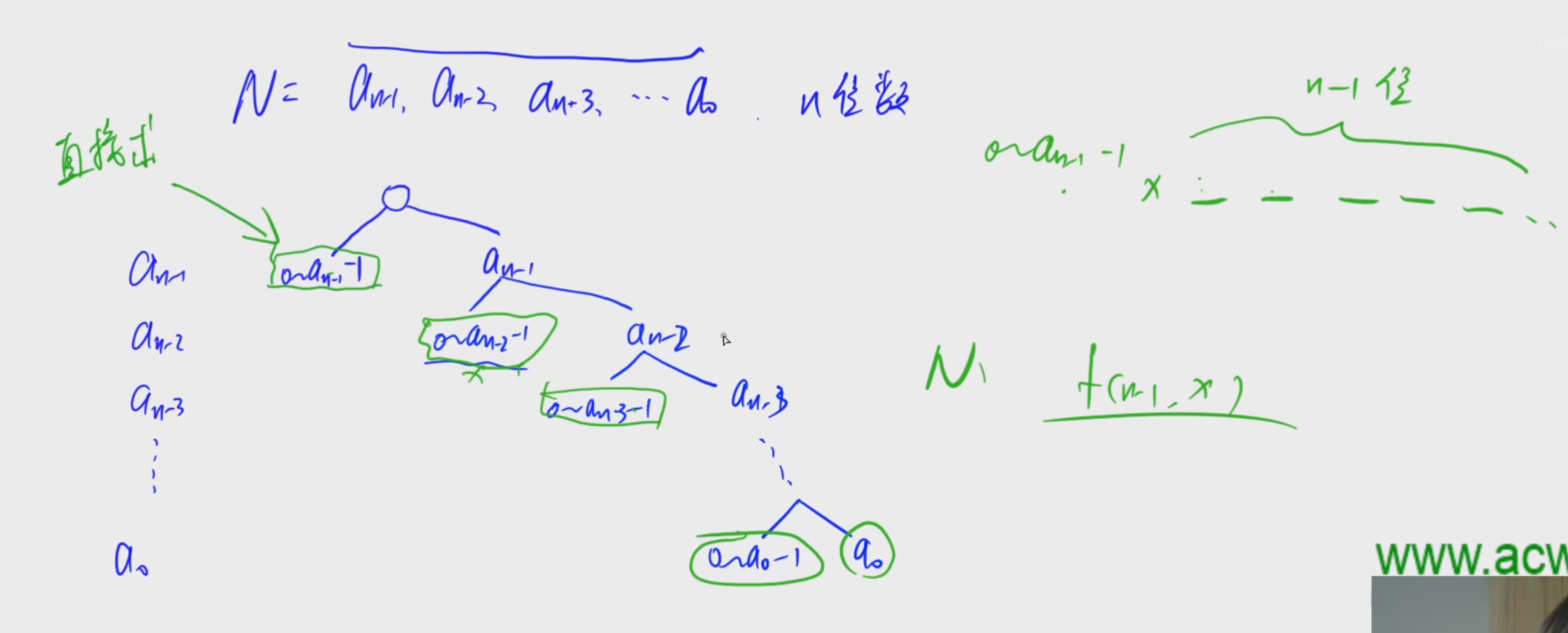
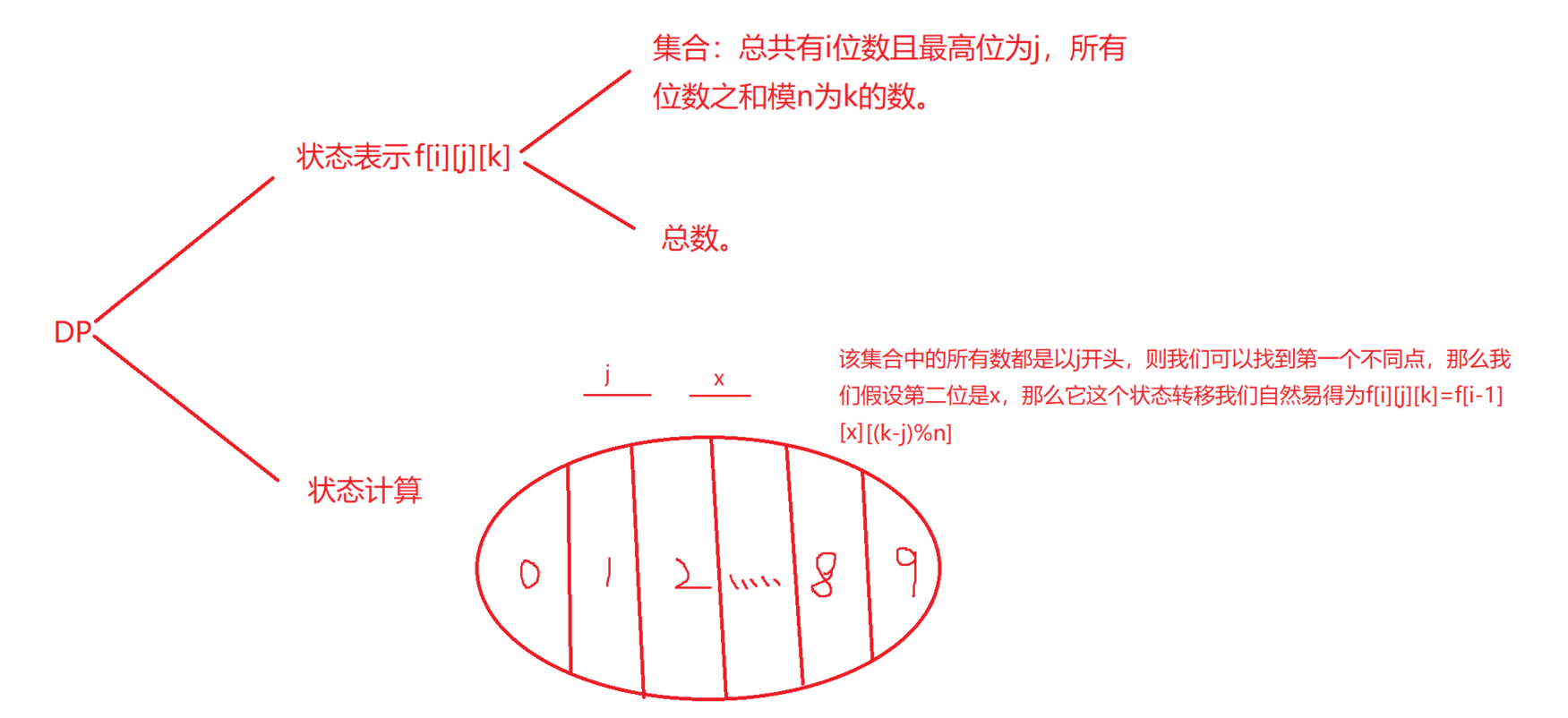
1、数位和

// 数位和#include<bits/stdc++.h>
using namespace std;
int c[21];
long long l, r, ans[10], f[17];inline void calc(long long n, int xs){  // xs : 系数int m = 0;           while(n){c[++m] = n % 10;n /= 10;}reverse(c + 1, c + 1 + m); // 3 2 4for(int i = 1; i <= m; ++i){// pos < ifor(int j = 1; j < i; ++j)ans[c[j]] += xs * c[i] * f[m - i];// pos = iif(i != 1 && c[i]) // c[i]的意思是c[i]这个数比0大  因为范围是  [0,c[i]),所以c[i]比0大，才考虑给0做贡献ans[0] += xs * f[m - i];for(int j = 1; j < c[i]; ++j)ans[j] += xs * f[m - i];// pos > iif(m > i){if(i != 1)ans[0] += xs * c[i] * f[m - i - 1] * (m - i);for(int j = 1; j < 10; ++j)ans[j] += xs * c[i] * f[m - i - 1] * (m - i);}}// 单独考虑第一类情况时，0的个数有多少个// 统计0的个数时，如果不单独考虑第一类的话，前导0也会被记入。  0000 - 9999   其实是 0 - 9999if(m > 1)ans[0] += xs * (c[1] - 1) * f[m - 2] * (m - 1);// 第1位非 0 的数字在第 j 位for(int j =  2; j < m ; ++j)ans[0] += xs * 9 * f[m - j - 1] * (m - j);
}int main(){f[0] = 1;for(int i = 1; i < 17; ++i)f[i] = f[i - 1] * 10;  // 存幂scanf("%lld%lld",&l,&r);calc(r + 1, 1);calc(l, -1);for(int i = 0; i <= 9 ; ++i)printf("%lld ", ans[i]);cout<<endl;return 0;
}

2、不要62


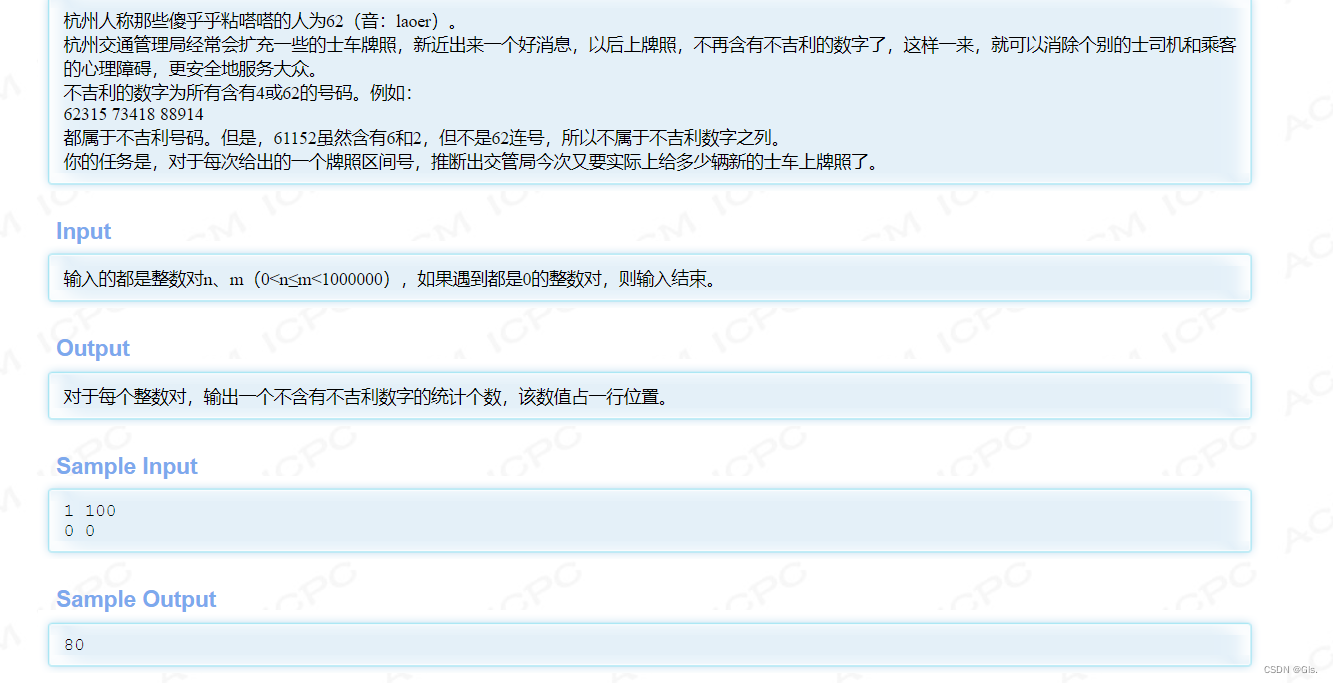
// 不要62
// #include <bits/stdc++.h>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
ll l, r, f[20][2];
int c[21];ll calc(ll n){int m = 0;memset(c,0,sizeof(c));while(n){c[++m] = n % 10;n /= 10;}reverse(c + 1, c + 1 + m);bool ok = true;ll res = 0;for(int i = 1; i <= m && ok; ++i){for(int j = 0; j < c[i]; ++j){memset(f,0,sizeof(f));if(j == 4 || (c[i - 1] == 6 && j == 2))continue;if(j == 6)f[i][1] = 1; // 前i位，第i位为6  则第二维为1elsef[i][0] = 1;for(int k = i + 1; k <= m; ++k)for(int sign = 0; sign < 2; ++sign)if(f[k - 1][sign])for(int l = 0; l < 10; ++l){if(l == 4 || (sign && l == 2))continue;if(l == 6)f[k][1] += f[k - 1][sign]; elsef[k][0] += f[k - 1][sign]; }res += f[m][0] + f[m][1];}if(c[i] == 4 || (c[i - 1] == 6 && c[i] == 2))ok = false;}return res;
}
int main(){while(~scanf("%lld %lld",&l, &r)){if(l == 0 && r == 0)break;cout << calc(r + 1) - calc(l) << endl;}return 0;
}

3、数数1

// 数数 1#include<bits/stdc++.h>
using namespace std;#define ll long long
ll l, r, f[21][10][2];
int c[21];inline ll calc(ll n){// 计算[1,n]满足条件的个数if(!n)return 0;// n如果等于0 ， 满足条件个数为0int m = 0;while(n){c[++m] = n % 10;n /= 10;}reverse(c + 1, c + 1 + m);bool ok = true;ll res = 0;for(int i = 1; i <= m && ok; ++i){// 第 i 类， 前 i - 1 位的数位值已经固定for(int j = 0; j < c[i]; ++j){// 第i位的值为jif(i != 1 && abs(j - c[i - 1]) > 2)continue;// 对于这部分的初始化问题，其实是这样的。/*比如说计算  12345 这个数字有多少是满足条件的，又比如说我们此时i = 3所以我们的j的取值范围是[0,2]当j = 0时：120 这个三位数是一个满足条件的数。所以f[3][0][1] = 1;此后的k 可以取到 4, 5 ，也就是说还要填 4,5这两个坑。而3这个位置的数可能取到[0,9]且sign可能是 0 , 1    这里的for循环只是罗列出很多的可能条件，可能很多是冗余的，但我们就是全部都考虑到了，冗余（不满足的部分）会因为判断条件而过滤掉*/memset(f,0,sizeof(f));if(i == 1 && !j)f[1][0][0] = 1;elsef[i][j][1] = 1;for(int k = i + 1; k <= m; ++k){// 后续还有 这么多个坑要填for(int l = 0; l < 10; ++l){// 前一位的数字的取值范围可能是[0,9]for(int sign = 0; sign < 2; ++sign){// 我们填写第k位时，是基于第k-1位满足条件的基础上！if(f[k - 1][l][sign]){ // 自己写的时候给漏了！！！for(int x = 0; x < 10; ++x){ //k 这个坑可以填的数字的范围是[0,9]if(sign && abs(x - l) <= 2)f[k][x][1] += f[k-1][l][1];if(!sign){if(x)f[k][x][1] += f[k - 1][0][0];elsef[k][0][0] += f[k - 1][0][0];}}}}}}for(int i = 0; i < 10; ++i)res += f[m][i][1];}// 如果出现125XXX  这样的情况， 因为后续的计算是基于前i为依据固定了的// 所以，后面的数字肯定不满足条件。  这是一个剪枝操作！ 去掉的话，结果也是对的。if(i != 1 && abs(c[i] - c[i-1]) > 2)ok = false; }if(ok)res++;return res;
}
int main(){scanf("%lld%lld",&l, &r);printf("%lld\n",calc(r) - calc(l - 1));return 0;
}

4、数数2

// 数数 2#include <bits/stdc++.h>
using namespace std;
#define ll long long
ll l, r, f[20][201];
bool b[201];
int c[21];
ll calc(ll n){ // 计算[1,n)符合条件的int m = 0;while(n){c[++m] = n % 10;n /= 10;}reverse(c + 1, c + 1 + m);ll res = 0;int sum = 0;for(int i = 1; i <= m; ++i){for(int j = 0; j < c[i]; ++j){memset(f,0,sizeof(f));f[i][sum + j] = 1;for(int k = i + 1; k <= m; ++k)for(int l = 0; l <= (k - 1) * 9; ++l)if(f[k - 1][l])for(int x = 0; x < 10; ++x)f[k][l + x] += f[k - 1][l];for(int k = 2; k <= 9 * m; ++k)if(!b[k])res += f[m][k];}sum += c[i];}return res;
}int main(){// ture : 合数   false ： 质数memset(b,false,sizeof(b));b[1] = true;for(int i = 2; i <= 200; ++i){if(!b[i])for(int j = i + i; j <= 200; j += i)b[j] = true;}cin >> l >> r;cout << calc(r + 1) - calc(l) << endl;	return 0;
}

5、数数3


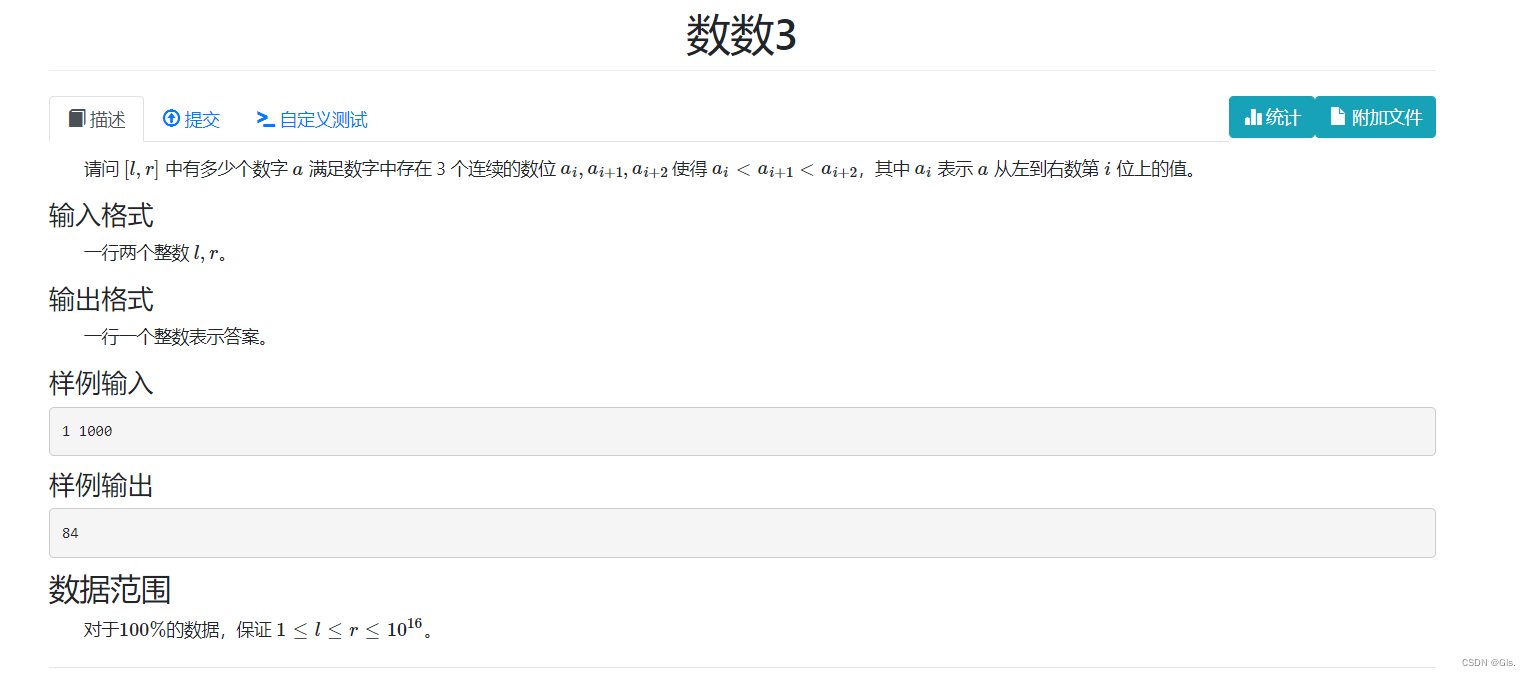
// 数数 3
#include <bits/stdc++.h>
using namespace std;
#define ll long long
// f[i][j][k][0..1] : 考虑了前 i 位，第 i 位的数字为 j ，前 i 位的状态为 k ，前 i 为是否全为0
// 0 这个状态表示
ll l, r, f[20][10][3][2]; 
int c[21];int get_status(int status, int x, int y){if(status == 2)return 2;if(x >= y)return 0;return status + 1;
}
ll calc(ll n){int m = 0;memset(c, 0 , sizeof(c));while(n){c[++m] = n % 10;n /= 10;}reverse(c + 1, c + 1 + m);ll res = 0;int status = 0; // 表示前 i - 1 位的状态for(int i = 1; i <= m; ++i){for(int j = 0; j < c[i]; ++j){int ns = get_status(status,c[i - 1], j); // next_status;if(i == 1)ns = 0;memset(f, 0, sizeof(f));if(i == 1 && j == 0)f[i][j][0][0] = 1;elsef[i][j][ns][1] = 1;for(int k = i + 1; k <= m; ++k){for(int w = 0; w < 10; ++w){ // 前一个数的数字范围for(int l = 0; l < 3; ++l){ // 前一个数的 状态可能for(int q = 0; q < 2; ++q){ // 前一个数 是否全为0 的情况可能if(f[k - 1][w][l][q]){for(int x = 0; x < 10; ++x){if(q == 0 && x == 0)f[k][0][0][0] += f[k - 1][0][0][0];else{if(q)f[k][x][get_status(l, w, x)][1] += f[k - 1][w][l][q];elsef[k][x][0][1] += f[k - 1][w][l][q];}}}}}}}for(int k = 0; k < 10; ++k)res += f[m][k][2][1];}if(i == 1)status = 0;elsestatus = get_status(status,c[i - 1], c[i]);}return res;}
int main(){cin >> l >> r;cout<< calc(r + 1) - calc(l) << endl;return 0;
}