数位dp

概述

数位是指把一个数字按照个、十、百、千等等一位一位地拆开，关注它每一位上的数字。如果拆的是十进制数，那么每一位数字都是 0~9，其他进制可类比十进制。

题目特征

数位 DP：用来解决一类特定问题，这种问题比较好辨认，一般具有这几个特征：

1. 要求统计满足一定条件的数的数量（即，最终目的为计数）；

2. 这些条件经过转化后可以使用「数位」的思想去理解和判断；

3. 输入会提供一个数字区间（有时也只提供上界）来作为统计的限制；

4. 上界很大（比如 ），暴力枚举验证会超时。

基本原理

考虑人类计数的方式，最朴素的计数就是从小到大开始依次加一。但我们发现对于位数比较多的数，这样的过程中有许多重复的部分。例如，从 7000 数到 7999、从 8000 数到 8999、和从 9000 数到 9999 的过程非常相似，它们都是后三位从 000 变到 999，不一样的地方只有千位这一位，所以我们可以把这些过程归并起来，将这些过程中产生的计数答案也都存在一个通用的数组里。此数组根据题目具体要求设置状态，用递推或 DP 的方式进行状态转移。

计数技巧

数位 DP 中通常会利用常规计数问题技巧，比如把一个区间内的答案拆成两部分相减（即 ${ans}_{[l,r]}={ans}_{[0,r]}-{ans}_{[0,l-1]}$

模板

# 假设n为b进制数
def dp(n) :# 特判数为0，如果是0则直接输出是否满足判断条件，后续不进行处理if not n : return ..nums = []while n :nums.append(n % b)n //= bres, last = 0, 0 #分别存储上结果和前面位中对当前位的有用信息for i in range(len(nums) - 1, -1, -1) : #对每一位进行枚举for j in 除上界以外可能的数 :if 进行可行性判断 :res += 预处理的数if 取上界不合法: break# 当判断最后一位时，直接判断取最后一位数是否可行，再计数。if not i and 判断是否可行 : res += 1return res

例题

度的数量

求给定区间 [X,Y] 中满足下列条件的整数个数：这个数恰好等于 K 个互不相等的 B 的整数次幂之和。

例如，设 X=15,Y=20,K=2,B=2，则有且仅有下列三个数满足题意：

17=24+20
18=24+21
20=24+22
输入格式
第一行包含两个整数 X 和 Y，接下来两行包含整数 K 和 B。

输出格式
只包含一个整数，表示满足条件的数的个数。

数据范围
1≤X≤Y≤231−1,
1≤K≤20,
2≤B≤10
输入样例：
15 20
2
2
输出样例：
3

思路

分类讨论，当枚举的位数处于第i位时$x_i$的情况，当N的第i位为x：

1. 当x = 0时：则$x_i$只能取0，即上界的情况，则继续向下枚举即可
2. 当x = 1时：则$x_i$取上界以外的情况只能是取0，此时低位的数可以随意填写，但必须满足题目中1的总个数等于k的前提下。随后取$x_i=1$，继续向低位枚举。
3. 当x > 1时：则$x_i$取上界以外的情况只可以是0、1，此时低位的数可以随意填写，但必须满足题目中1的总个数等于k的前提下。但$x_i$永远碰不到上界，则无需向低位枚举。

注意：当枚举到第i位时，已经使用了last个1，如果是未取上界的情况，那么剩下的i位低位中剩余k-last个1可用随便放。是个组合数，可以预处理出来。

代码

N = 35
f = [[0] * N for _ in range(N)]def init() : #预处理出组合数for i in range(N) :for j in range(N) :if j == 0 :f[i][j] = 1else :f[i][j] = f[i - 1][j - 1] + f[i - 1][j]def dp(n) :# 特判0if not n : return 0nums = []#处理出n在b进制下的每一位的数while n : nums.append(n % b)n //= bres, last = 0, 0 #分别记录结果和高位对1的使用情况for i in range(len(nums) - 1, -1, -1) : #从高位往低位枚举x = nums[i] #取出n中第i位的数if x : #当0不是上界res += f[i][k - last] #第i位为0的情况#当上界大于1的情况，可取1if x > 1 :if k - last - 1 >= 0 : res += f[i][k - last - 1]break# 取上界为1时else :last += 1if last > k : breakif not i and last == k : res += 1return resinit()			
l, r = map(int, input().split())
k = int(input())
b = int(input())
print(dp(r) - dp(l - 1))

数字游戏

科协里最近很流行数字游戏。

某人命名了一种不降数，这种数字必须满足从左到右各位数字呈非下降关系，如 123，446。

现在大家决定玩一个游戏，指定一个整数闭区间 [a,b]，问这个区间内有多少个不降数。

输入格式
输入包含多组测试数据。

每组数据占一行，包含两个整数 a 和 b。

输出格式
每行给出一组测试数据的答案，即 [a,b] 之间有多少不降数。

数据范围
1≤a≤b≤231−1
输入样例：
1 9
1 19
输出样例：
9
18

思路

分类讨论，当枚举的位数处于第i位时$x_i$的情况，当N的第i位为x：

1. 当$x_i=x$时，即取上界时，如果合法，则继续向更低位开始枚举。
2. 当$x_i<x$时，则更低位的数应该是所有以$[last,x)$为最高位的i + 1位数的非下降的数

last为上一位的上界即$x_{i+1}$

预处理：
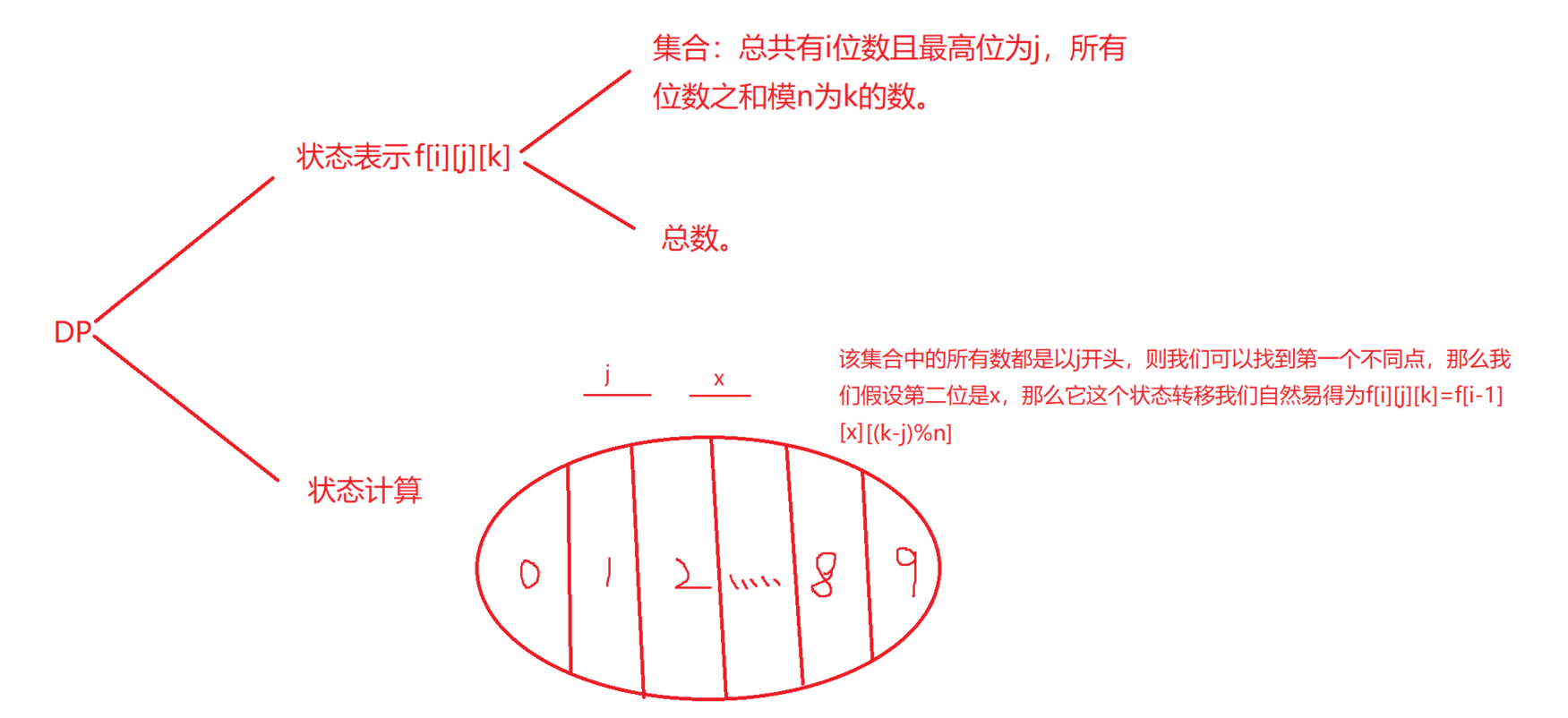
状态表示：
集合：f[i, j]表示最高位为j的i位的非下降的数的集合
属性：num
状态计算：$f[i,j]={\sum }_j^{9}f[i-1,k]$

代码

N = 15f = [[0] * N for _ in range(N)]# 预处理出最高位为j的i位的非下降的数的数量
def init() :for i in range(10) : f[1][i] = 1for i in range(2, N) :for j in range(10) :for k in range(j, 10) :f[i][j] += f[i - 1][k]def dp(n) :# 特判0，有一个数满足条件if not n : return 1nums = []#处理出n的每一位，存于nums中while n :nums.append(n % 10)n //= 10res, last = 0, 0 #last存储上一层的数# 从高到低枚举每一位for i in range(len(nums) - 1, -1, -1) :x = nums[i]if last > x : break #如果当前位能取到的最大的数小于上一层上界，则退出#x_i不取上界for j in range(last, x) :res += f[i + 1][j]#取上界last = xif not i : res += 1 #特判最后一个数return resinit()
while True :try :l, r = map(int, input().split())except : breakprint(dp(r) - dp(l - 1))

不要62

杭州人称那些傻乎乎粘嗒嗒的人为 62（音：laoer）。

杭州交通管理局经常会扩充一些的士车牌照，新近出来一个好消息，以后上牌照，不再含有不吉利的数字了，这样一来，就可以消除个别的士司机和乘客的心理障碍，更安全地服务大众。

不吉利的数字为所有含有 4 或 62 的号码。例如：62315,73418,88914 都属于不吉利号码。但是，61152 虽然含有 6 和 2，但不是 连号，所以不属于不吉利数字之列。

你的任务是，对于每次给出的一个牌照号区间 [n,m]，推断出交管局今后又要实际上给多少辆新的士车上牌照了。

输入格式
输入包含多组测试数据，每组数据占一行。

每组数据包含一个整数对 n 和 m。

当输入一行为“0 0”时，表示输入结束。

输出格式
对于每个整数对，输出一个不含有不吉利数字的统计个数，该数值占一行位置。

数据范围
1≤n≤m≤109
输入样例：
1 100
0 0
输出样例：
80

思路

分类讨论，当枚举的位数处于第i位时$x_i$的情况，当N的第i位为x：

1. 当$x_i=x$时，即取上界时，如果合法（不等于4且last与$x_i$不等于62），则继续向更低位开始枚举。
2. 当$x_i<x$时，则更低位的数应该是所有以$[0,x)$为最高位的i + 1位数合法的数

last为上一位的上界即$x_{i+1}$

预处理：
状态表示：
集合：f[i, j]表示最高位为j的i位的吉利的号码的集合
属性：num
状态计算：$f[i,j]={\sum }_0^{9}f[i-1,k]$

代码

N = 10f = [[0] * N for _ in range(N)]
# 预处理 f[i, j]表示最高位为j的i位的吉利的号码的集合的数目
def init() :for i in range(10) :if i == 4 : continuef[1][i] = 1for i in range(2, N) :for j in range(10) :if j == 4 : continuefor k in range(10) :if k== 4 or (j == 6 and k == 2) : continuef[i][j] += f[i - 1][k]def dp(n) :if not n : return 1nums = []while n :nums.append(n % 10)n //= 10res, last = 0, 0# 从高到低枚举每一位for i in range(len(nums) - 1, -1, -1) :x = nums[i]# x_i不取上界for j in range(x) :# 判断是否合法if j == 4 or (last == 6 and j == 2) :continueres += f[i + 1][j]# 当取上界x不合法时，则退出if x == 4 or (last == 6 and x == 2) : breaklast = x# 特判数为n时if not i : res += 1return res
init()
while True :l, r = map(int, input().split())if l == 0 and r == 0 : breakprint(dp(r) - dp(l - 1))