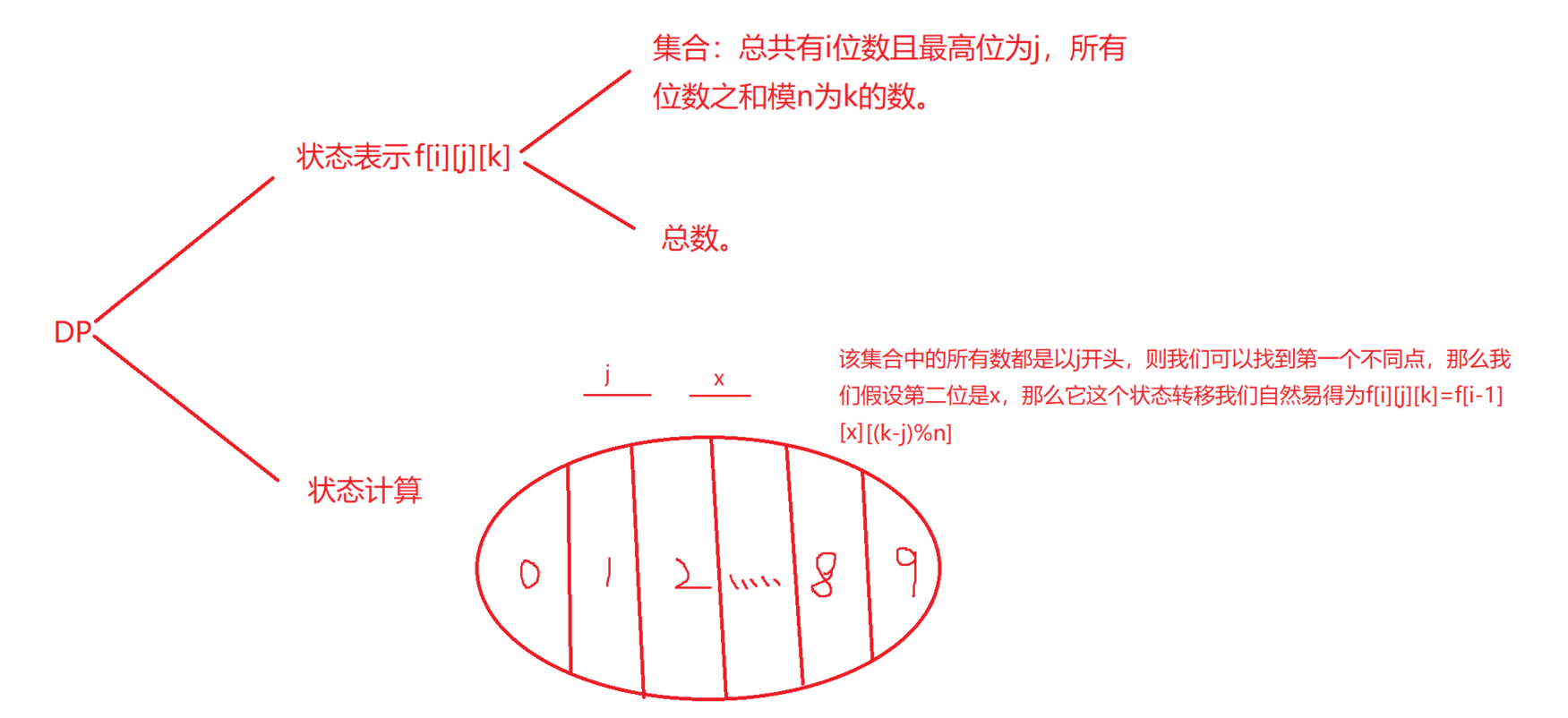
数位DP用来解决什么问题？

我们有时候会遇到这样一类题目，给你一个区间 [l,r] ，找区间上符合某种特定要求的数的个数，这个要求可能很简单，很好理解，但是由于区间范围太大，以至于对每个数进行遍历判别是不太可能的，对于这种情况，就需要用数位DP来解决了。

朴素解法

for(int i = l;i<=r;i++)if(check(i))ans++;

其中check函数是检验是否满足要求，ans是总个数，这样求解很容易超时，比如 l = 1，r = 1e9，时间上肯定是过不去的，于是我们就要考虑如何优化这个问题了。

两个优化思想

思想1：用f(x)表示不大于x的数中满足要求的个数，这样最后的结果可以表示为：f(r) - f(l-1)
思想2：用一棵树的形式来理解

这里说的可能有点抽象了，但是没有关系，我们以一道题目为例：给定一个区间 [l.r] ，找到这个区间上所有的“不减数”，不减数定义为从高位到低位数字大小是不减的，比如：223,669,456等等

那么这道题目我们首先使用第一个思想，假设dp(n)为区间 [0,n] 上的不减数的个数，那么最后的结果应该是dp(r) - dp(l-1)，下边我们来详细介绍一下第二个优化思想，我们将数字n各位上的数字从高位到低位排列，如下图所示：

我们很容易能够理解，题目中要求的数实际上满足：

我们假设：f[i,j] 表示最高位为j，长度为i的数中，不降数的个数，所以我们有代码：

void init()
{//长度为1的个数只有一个for(int i=0;i<=9;i++) f[1][i]=1;//长度大于1时for(int i=2;i<maxn;i++)//枚举开头元素for(int j=0;j<=9;j++)for(int k=j;k<=9;k++)//将以k开头，长度为i的数放在数字j后边形成新的不降数f[i][j]+=f[i-1][k];
}

下边我们考虑数位，我们将这个数字竖着来写，当我们选择数字时，比如当n=5863时，那么最高位就是5，很明显我们只能取0~5，下边我们将分两种情况，第一种是取0~4，此时只要以0~4开头的所以数是存在的，于是f[0~4][m]就是该部分的不降数个数；对于另一种情况，最高位取了5，那么下一位并不能取遍0~9，所以需要再做一次分类。

如下图所示，当第二位取0~7时，那么后边的数字可以取遍0~9，所以满足条件个数为 f[0~7,m-1]，对于取8的情况，还要继续分情况，到这里就很清楚的说明为什么数位DP可以用一颗树来形象说明了，中间过程是递归的，下边我给出解题代码：

题解

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
const int maxn=15;int f[maxn][maxn];void init()
{//长度为1的个数只有一个for(int i=0;i<=9;i++) f[1][i]=1;//长度大于1时for(int i=2;i<maxn;i++)//枚举开头元素for(int j=0;j<=9;j++)for(int k=j;k<=9;k++)//将以k开头，长度为i的数放在数字j后边形成新的不降数f[i][j]+=f[i-1][k];
}int dp(int n)
{if(!n) return 1;vector<int>nums;while(n) nums.push_back(n%10),n/=10;int res=0;//方案数int last=0;//保留一些前缀信息，本题是上一个数是几///从最大数开始枚举for(int i=nums.size()-1;i>=0;i--){int x=nums[i];//x为当前这位数for(int j=last;j<x;j++)  要保障比下一位>=上一位，所以从last开始枚举,最多枚举到x,last为上一位，也即最高位，对下一位的枚举是有限制的res+=f[i+1][j];    ///左端的节点有i+1个位数（因为第一位的下标是0)if(x<last) break;//如果当前这位数比上一位小，那么后面的都不成立了，直接break退出last=x;if(!i) res++; //如果能顺利到最后一个数说明树的最右边这一段的每一个数都是小于等于前一位数的，因而++}return res;
}int main(void)
{init();int l,r;while(cin>>l>>r){cout<<dp(r)-dp(l-1)<<endl;}return 0;    
}

不理解模板？再来一道题目

题目链接：https://www.acwing.com/problem/content/1083/

这里还是解释一下题意：求符合要求的数的个数，要求为一个数字可以被表达为以下形式：

其中n和a代表一个数字，m1~mp是p个不同的数字，换言之，一个数字n可以写成a的不同幂的和，那么这个数字就是符合要求的。还是给一个区间 [l,r] 求区间中所有符合要求的数字的个数，我们可以将这道题目题解为，将n转换为a进制，该数字中各个位上1个个数正好有K个，我们定义 f[i,j] 代表后i位中包含j个1的数字的个数，初始化过程为：

void init(){for(int i = 0;i<=N;i++)for(int j = 0;j<=i;j++)if(!j)f[i][j] = 1;else f[i][j] = f[i-1][j]+f[i-1][j-1];
}

我还先将流程放上来：

如果当前位是0的话，那么该位只能取0，有res += f[i][K - last]，last是已经使用了多少个1，如果当前为为1的话，那么last++；如果当前位大于1的话后边的数字将不受限制，res += f[i][K-last-1];break终止即可，下边是详细代码：

题解

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;int X,Y,K,B;
const int N = 35;
int f[N][N];//组合数
//f[i][j]表示i个数中随机先j个的组合数
void init(){for(int i = 0;i<=N;i++)for(int j = 0;j<=i;j++)if(!j)f[i][j] = 1;else f[i][j] = f[i-1][j]+f[i-1][j-1];
}int dp(int n){//特判if(n==0)return 0;//转化为B进制vector<int>nums;while(n){nums.push_back(n%B);n = n/B;}int res = 0;int last = 0;for(int i = nums.size()-1;i>=0;i--){int x = nums[i];//如果x>0if(x){//该位取0res += f[i][K - last];if(x>1){//大于1，后边取值不受限制，终止if(K-last-1>=0)res += f[i][K-last-1];break;}else {//等于1，用掉一个1last++;if(last>K)break;}}//特判if(i==0&&last==K)res++;}return res;
}int main(){init();cin>>X>>Y>>K>>B;cout<<dp(Y)-dp(X-1)<<endl;return 0;
}