Sparsity constraint稀疏约束详解
引子： 线性模型是我们经常使用的一种模型，比如：
文本分类中，bag-of-words 有p = 20 K 个特征， 共有 N = 5K 个文本样例；
在图像去模糊化，图像分类中，有p=65K 个像素点特征，N=100个样例；
等等
这些问题我们都可以使用线性模型解决，比如线性回归，logistic回归， Cox 回归来解决。 因为 p 远大于 N，所以必须引入正则化。
为什么这里要用正则化呢？
以我们很熟悉的线性回归模型为例：线性回归问题事实上是一个最小二乘问题（ A least-squares problem ），目标函数为：
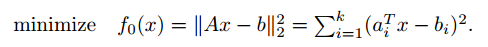
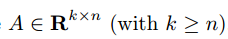，其中 
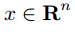是所要求的参数， 注：这里表述使用Convex Optimization book的描述，与通常的稍有不同，
事实上 x 相当于我们常说的参数 w
上式可以化为：
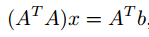
从而我们可以得到它的解析解：
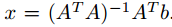
看起来好像很简单，但是存在一个问题，我们在求最优解时，即最小化f(x)时，若Ax - b 是不可逆的，则求导且令导数为0后方程有无穷解。事实上我们求导置为0后
得到的就是一个线性等式的集合，利用我们学过的线性代数的知识，即求一个齐次线性方程组的解，当方程组数小于参数数量时，或者说线性方程组对应的系数矩阵的行
数小于列数时，有无穷多解。所以我们前面所说的p对应于系数矩阵的行，样本数对应于系数矩阵的列，所以此时无法求出最优解。而且此时也出现过拟合的问题。
其实在实际中我们经常遇到这种情况：变量数（样本维度）远大于样本数目的情况，样本数目太少不足以估计出所有的所要求的系数。
我们可以基于两个思路来考虑：
首先，如此多的参数（特征）是否都与我们要求的结果有关系呢，或者说是不是有些变量（特征）对我们结果并没有影响或影响非常小可以忽略不计；
另一方面来考虑，对参数w 我们可以求出无穷多解，这个解空间太大了，我们能不能给它一个约束，使解空间大大缩小，或者说在新的解空间里能够找到最优解。
通常的解决方法是：
(1) Forward stepwise
(2) Best-subset
(3) Ridge regression
(4) Lasso regression
其中(4)即用到了我们所要探究的稀疏约束，所以我们来看看Lasso regression 回归到底是什么：
其实就是对我们的模型加了这样一个约束条件：
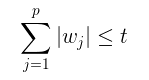
即Lasso 是在线性模型上加了一个L1正则化项：
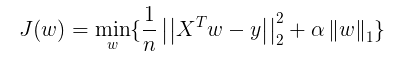
为了说明稀疏性，我们也来看下方法(3) Ridge regression：
它是对模型加了这样一个约束条件：
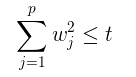
即Ridge 是在线性模型上加了一个L2正则化项：
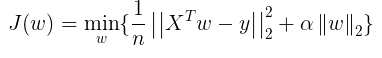
Ridge 仅仅对变量进行了收缩（shrinkage），但是Lasso 既对变量进行了选择，也进行了收缩，如下图所示：
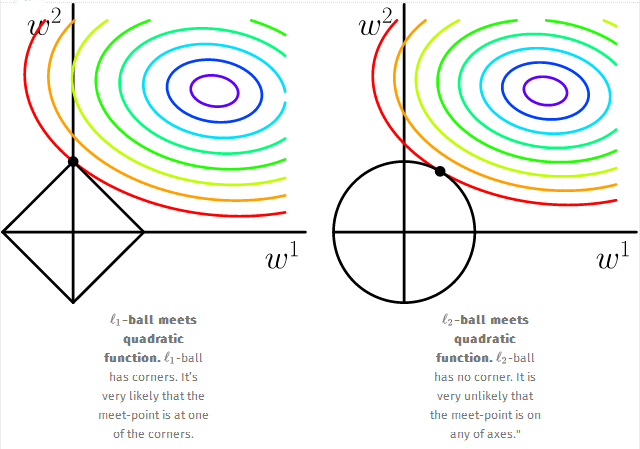
看上图，相交之处即所求解；看左图，圆很容易与约束区域的角相交，此时w1为0，对于一个更高维的情况，很可能有很多会有更多地
wi为0的情况，这也意味着我们对变量进行了选择，由此造成了稀疏性。而对于右图，在坐标轴上相交的概率会远小于前者，很难形成
稀疏性。
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
回顾一下L1 正则化的历史：
首先，David L. Donoho 和 Iain M. Johnstone 在1994年发表的论文”小波软阈值去噪“中首次使用了类似于L1的公式：
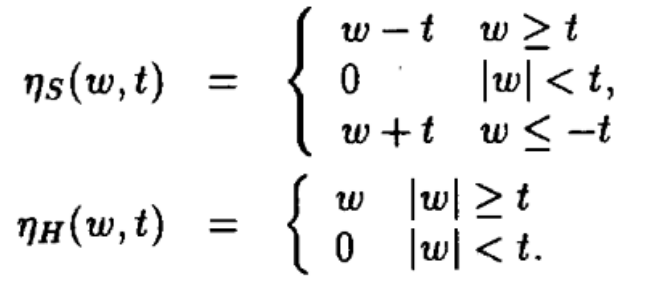
论文地址：http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=412133
随后1995年，Tibshirani 将Lasso 应用于回归问题中，而且给出了详细的解释，
论文地址：https://statweb.stanford.edu/~tibs/lasso/lasso.pdf
此后，Tibshirani 又将Lasso应用于几个其他的模型，如Logistics回归。
Donoho2004, CandesandTao2005 又将lasso应用于压缩感知之中。
---------------------------------------------------------------------------------------------------
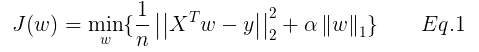
很明显Eq.1是一个凸函数，存在最优解，但是注意到L1正则化项并不是可导的，亦即不可导的凸函数求最优解问题，该如何解决呢？目前主要有6种解决方法：
（1）将不平滑问题转化为平滑问题
（2）坐标下降法 （coordinate descend）
（3）ADMM算法
（4）次梯度下降法（subgradient）
（5）梯度下降
（6）加速梯度下降
我们来看次梯度方法，次梯度的定义如下：
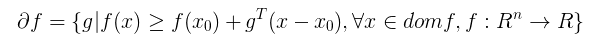
怎么理解次梯度呢？若 f(x) 是一个凸函数，且在x0 处可导 ， 则由一阶泰勒展开式，可得：
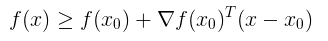
若f(x) 在x0处 不可导，我们仍然可以得到f(x)的一个下界：
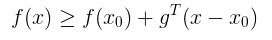
以下面的函数为例：
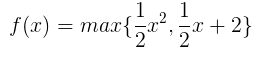
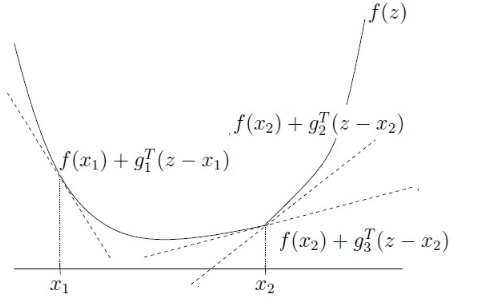
在x1 点 函数可导，此时次梯度与导数相同，只有一个；在x2点，函数不可导，此时次梯度不止有一个，次梯度的取值范围是一个闭区间。
由此我们求解的思路是：对于可导的地方，按照常规方法直接求导求解即可；对于不可导的地方，使用次梯度。下面来求目标函数Eq.1的最优解：
不考虑正则化项，由前面说过的最小二乘法，我们有：
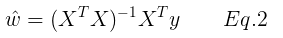
简单起见，我们只考虑标准正交化的情况，即有：
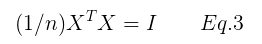
将Eq.3 代入 Eq.2 可得：
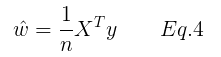
假设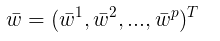 
是 J(w) 的全局最优解， 考虑第 j 个 变量
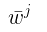，存在两种可能：
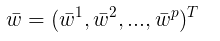是 J(w) 的全局最优解， 考虑第 j 个 变量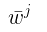，存在两种可能： （1）梯度存在时候，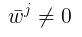 
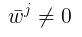，我们有：
，我们有：
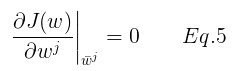
由Eq.5 可得：
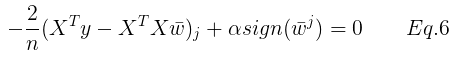
将Eq.3 和 Eq.4 代入Eq.6 得：
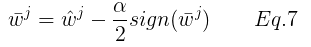
sign是符号函数，易得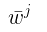和 
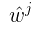同号（假设符号后计算下即可证明），从而有
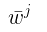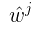和 同号（假设符号后计算下即可证明），从而有
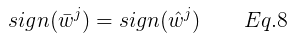
将Eq.8 代入 Eq.7 得：
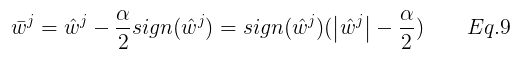
在利用 Eq.8 ，然后两边同乘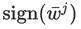 
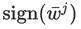，可得：
，可得：
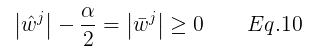
由 Eq.10 和 Eq.9可得：
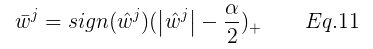
这里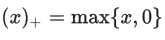 
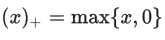
（2）当梯度不存在时，即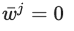 
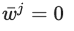时，有：
时，有：
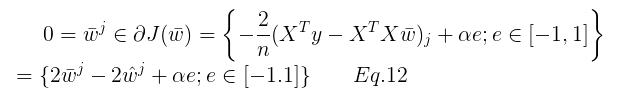
这里用到了一个性质：点x0 是凸函数 f 的一个全局最小值点，当且仅当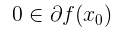 
。（注：这里上式没有给出具体的迭代求解过程）。可得：
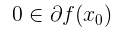。（注：这里上式没有给出具体的迭代求解过程）。可得：
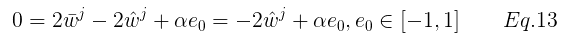
由Eq.13 得：
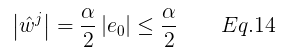
由此可得，Eq.14 同样满足Eq.11，于是两种情况都可以用Eq.11 表示，所以Eq.1的最优解可以使用Eq.11表示。
参考：
http://blog.csdn.net/lansatiankongxxc/article/details/46386341
http://freemind.pluskid.org/machine-learning/sparsity-and-some-basics-of-l1-regularization/#d20da8b6b2900b1772cb16581253a77032cec97e
ttps://web.stanford.edu/~hastie/TALKS/Sparsity.pdf
![[VLDB 2022]Butterfly Counting on Uncertain Bipartite Graphs](https://img-blog.csdnimg.cn/img_convert/1b73ccd0e116142bc0cca4fe865cd11b.png)
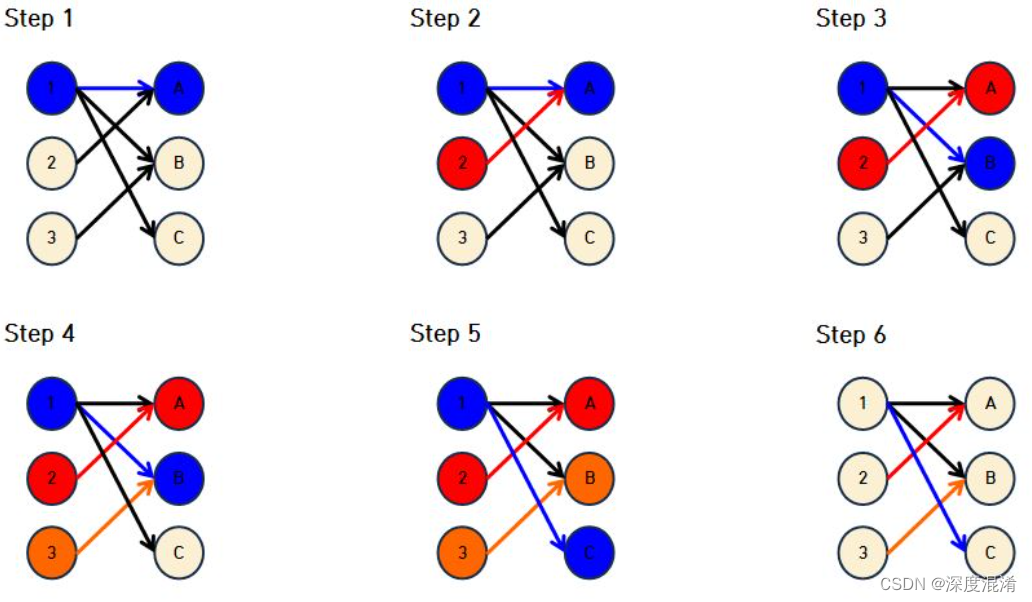
![二分匹配大总结——Bipartite Graph Matchings[LnJJF]](https://img-blog.csdnimg.cn/f12f5708538c44c08101ac60cf3d8342.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBATG5KSkY=,size_20,color_FFFFFF,t_70,g_se,x_16)
