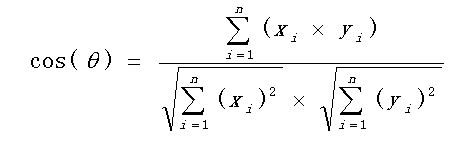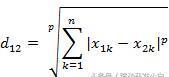文章目录
- 一、理论基础
- 二、案例背景
- 1、问题描述
- 2、解决思路及步骤
- (1). 算法流程
- (2). 算法实现过程
- 三、MATLAB程序实现
- 1、程序源码
- 2、结果分析
- 四、参考文献
一、理论基础
TSP(traveling salesman problem,旅行商问题)是典型的NP完全问题,即其最坏情况下的时间复杂度随着问题规模的增大按指数方式增长,到目前为止还未找到一个多项式时间的有效算法。
TSP问题可描述为:已知 n n n个城市相互之间的距离,某一旅行商从某个城市出发访问每个城市有且仅有一次,最后回到出发城市,如何安排才使其所走路线距离最短。简言之,就是寻找一条最短的遍历 n n n个城市的路径,或者说搜索自然子集 X = { 1 , 2 , ⋯ , n } X=\{1,2,\dotsm,n\} X={1,2,⋯,n}( X X X的元素表示对 n n n个城市的编号)的一个排列 π ( X ) = { V 1 , V 2 , ⋯ , V n } π(X)=\{V_1,V_2,\dotsm,V_n\} π(X)={V1,V2,⋯,Vn},使得 T d = ∑ i = 1 n + 1 d ( V i , V i + 1 ) + d ( V n , V 1 ) T_d=\sum_{i=1}^{n+1} {d(V_i,V_{i+1})}+d(V_n,V_1) Td=i=1∑n+1d(Vi,Vi+1)+d(Vn,V1)取得最小值,其中 d ( V i , V i + 1 ) d(V_i,V_{i+1}) d(Vi,Vi+1)表示城市 V i V_i Vi到城市 V i + 1 V_{i+1} Vi+1的距离。
二、案例背景
1、问题描述
假设有一个旅行商人要拜访某些城市,他需要选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择要求是:所选路径的路程为所有路径之中的最小值。
具体城市个数及位置可参考:
链接:https://pan.baidu.com/s/1eJZXhoM8hjvp-3UGhzYZQw
提取码:wxyz
其中一个城市位置分布图如图1所示。

2、解决思路及步骤
(1). 算法流程
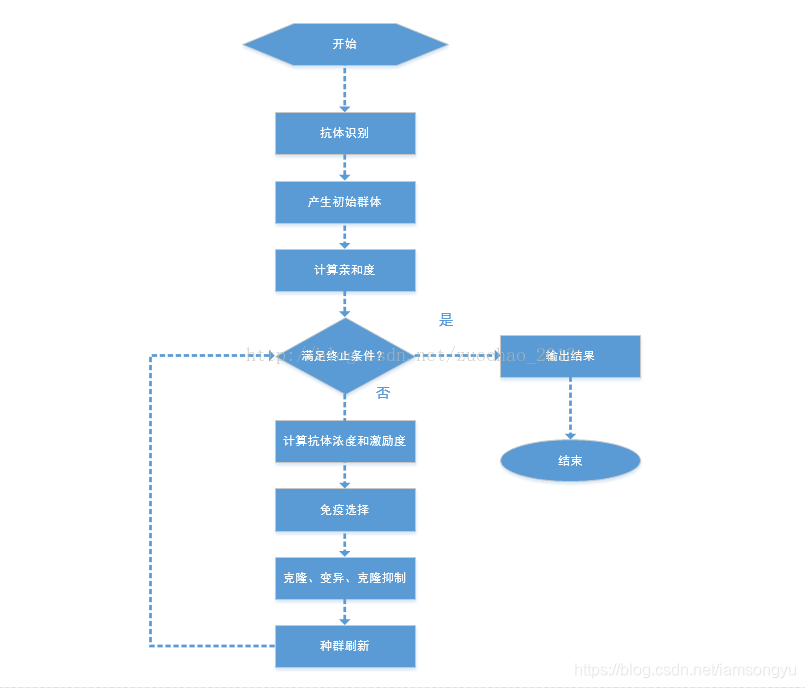
免疫优化算法求解TSP问题的流程如图2所示。

(2). 算法实现过程
(1)初始化免疫个体维数为城市个数 N N N,免疫种群个体数为 N P = 200 NP=200 NP=200,最大免疫代数为 G = 1000 G=1000 G=1000,克隆个数为 N c l = 10 Ncl=10 Ncl=10,计算任意两个城市间的距离矩阵 D D D。
(2)随机产生初始种群,计算个体亲和度(即路径距离),并按亲和度升序排列。
(3)在取亲和度前对 N P / 2 NP/2 NP/2个个体进行克隆操作,并对每个源个体产生的克隆个体进行任意交换两个城市的变异操作;然后计算其亲和度,进行克隆抑制操作,只保留亲和度最高的个体,从而产生新的免疫种群。
(4)随机生成 N P / 2 NP/2 NP/2个个体的新种群,并计算个体亲和度;免疫种群和随机种群合并,按亲和度排序,进行免疫迭代。
(5)判断是否满足终止条件:若满足,则结束搜索过程,输出优化值;若不满足,则继续进行迭代优化。
三、MATLAB程序实现
1、程序源码
- 计算路径长度函数
function len = PathLength(D, Chrom)
%% 计算各个体的路径长度
% 输入:
% D 两两城市之间的距离
% Chrom 个体的轨迹
[row, col] = size(D);
NIND = size(Chrom,1);
len = zeros(NIND,1);
for i = 1:NINDp = [Chrom(i,:) Chrom(i,1)];i1 = p(1:end-1);i2 = p(2:end);len(i, 1) = sum(D((i1-1)*col+i2));
end
- 输出路径信息的函数
function p = OutputPath(R)
%% 输出路径函数
%输入:R 路径
R = [R, R(1)];
N = length(R);
p = num2str(R(1));
for i = 2:Np = [p,'—>',num2str(R(i))];
end
disp(p)
- 画出路线轨迹图的函数
function DrawPath(Chrom,X)
%% 画路径函数
% 输入
% Chrom 待画路径
% X 各城市坐标位置
R = Chrom(1, :); % 一个随机解(个体)
n = size(X, 1);
figure;
plot([X(R(1), 1), X(R(n), 1)], [X(R(1), 2) ,...X(R(n), 2)], 'ms-', 'LineWidth', 2, 'MarkerEdgeColor', 'k', 'MarkerFaceColor', 'g')
hold on
for i = 2:nplot([X(R(i-1), 1),X(R(i), 1)], [X(R(i-1), 2),...X(R(i), 2)], 'ms-', 'LineWidth', 2, 'MarkerEdgeColor', 'k', 'MarkerFaceColor', 'g')hold on
end
plot(X(R(1), 1), X(R(1), 2), 'bv', 'MarkerSize', 20)
plot(X(R(end), 1), X(R(end), 2), 'bs', 'MarkerSize', 20)
text(X(R(1),1)+0.03, X(R(1),2)+0.03, [' 起点' num2str(R(1))], 'color', [1,0,0]);
text(X(R(end),1)+0.03, X(R(end),2)+0.03, [' 终点' num2str(R(end))], 'color', [1,0,0]);
for i = 1:size(X,1)if R(1) ~= i && R(end) ~= itext(X(i,1)+0.03, X(i,2)+0.03, num2str(i), 'color', [0,0,0]);end
end
grid on
xlabel('横坐标')
ylabel('纵坐标')
title('轨迹图')
- 主函数
clear;
clc;
%% 加载数据,画出城市位置
load CityPosition3.mat
figure;
plot(X(:, 1), X(:, 2), 'ms', 'LineWidth', 2, 'MarkerEdgeColor', 'k', 'MarkerFaceColor', 'g')
for i = 1:size(X, 1)text(X(i, 1)+0.03, X(i, 2)+0.03, num2str(i));
end
legend('城市位置')
title('城市分布图', 'fontsize', 12)
xlabel('km', 'fontsize', 12)
ylabel('km', 'fontsize', 12)
grid on;
%% 初始化参数
N = size(X, 1); % 城市数量
D = zeros(N); % 距离矩阵
% 求任意两个城市距离间隔矩阵
for i = 1:Nfor j = i+1:ND(i, j) = sqrt(sum((X(i, :)-X(j, :)).^2));D(j, i) = D(i, j); % 利用D是对称矩阵的性质end
end
NP = 200; % 免疫个体数目
G = 1000; % 最大免疫代数
Chrom = zeros(NP, N); % 种群
% 初始化种群
for i = 1:NPChrom(i, :) = randperm(N); % 随机生成初始种群
end
len = PathLength(D, Chrom); % 各个体路径长度
[Sortlen, Index] = sort(len);
SortChrom = Chrom(Index, :); % 种群个体排序
gen = 1; % 免疫代数初值
Ncl = 10; % 克隆个数
%% 画出随机解的路线图
DrawPath(Chrom(1, :), X);
%% 输出随机解的路线和总距离
disp('初始种群中的一个随机值:')
OutputPath(Chrom(1,:));
Rlength = PathLength(D,Chrom(1,:));
disp(['总距离:', num2str(Rlength)]);
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')
%% 免疫算法迭代优化
while gen<Gfor i = 1:NP/2%% 选亲和度前NP/2个个体进行免疫操作c = SortChrom(i, :);chrom = repmat(c, Ncl, 1);for j = 1:Nclwhile 1p1 = floor(1+N*rand());p2 = floor(1+N*rand());if p1 ~= p2break;endendtemp = chrom(j, p1);chrom(j, p1) = chrom(j, p2);chrom(j, p2) = temp;endchrom(1, :) = SortChrom(i, :); % 保留克隆源个体 %% 克隆抑制,保留亲和度最高的个体chromLen = PathLength(D, chrom);[SortChromLen, index] = sort(chromLen);Sortchrom = chrom(index, :);ch(i, :) = Sortchrom(1, :);chLen(i) = SortChromLen(1);end%% 种群更新for i = 1:NP/2rc(i, :) = randperm(N); % 随机生成种群end rcLen = PathLength(D, rc); % 计算路径长度%% 免疫种群与新种群合并Chrom = [ch; rc];len = [chLen'; rcLen];[Sortlen, index] = sort(len);SortChrom = Chrom(index, :);% 迭代次数加1,记录最优值trace(gen) = Sortlen(1);gen = gen+1;
end
%% 画出最优解的路线图
ShortestPath = SortChrom(1, :); % 最优路径
ShortestLength = trace(end); % 最短距离
DrawPath(ShortestPath, X)
figure;
plot(trace, 'r', 'LineWidth', 2);
xlabel '迭代次数'; ylabel '路径距离';
title '亲和度进化曲线';
%% 输出最优解的路线和总距离
disp('最优路线:')
p = OutputPath(ShortestPath);
disp(['最短距离:', num2str(ShortestLength)]);
disp('-------------------------------------------------------------')
2、结果分析
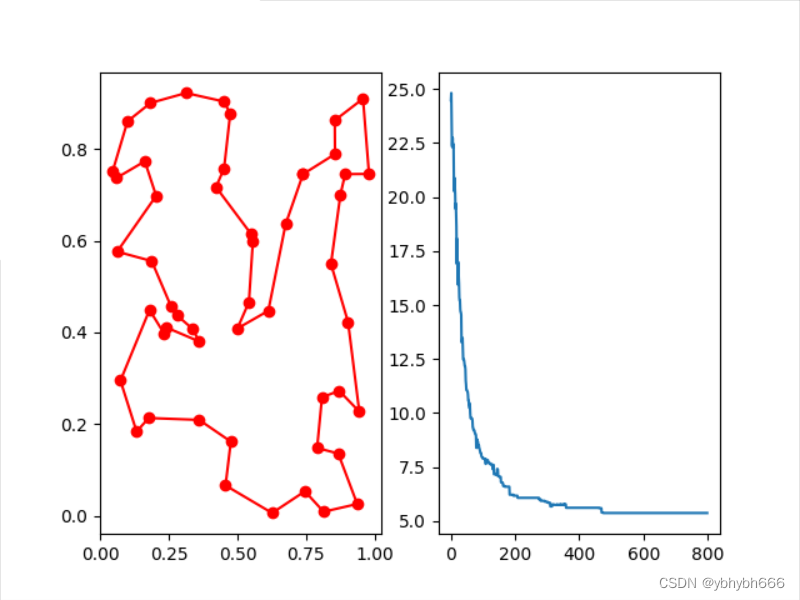
优化前的一个随机路线轨迹图如图3所示。

初始种群中的一个随机值:
20—>31—>18—>25—>8—>9—>7—>19—>27—>10—>2—>26—>16—>1—>6—>15—>28—>13—>14—>22—>17—>3—>21—>23—>12—>4—>29—>11—>30—>24—>5—>20
总距离:42.7564
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
优化后的路线轨迹如图4所示。


最优路线:
14—>12—>13—>7—>5—>2—>10—>9—>8—>4—>16—>6—>11—>23—>20—>21—>22—>18—>3—>17—>19—>24—>25—>26—>28—>27—>30—>31—>29—>1—>15—>14
最短距离:15.9262
-------------------------------------------------------------
由优化图可以看出,优化前后路径长度得到很大改进,接近300代后路径长度已经保持不变了,可以认为是最优解了,总距离由优化前的42.7564减少到优化后的15.9262,减为原来的37.2%。
四、参考文献
[1] 凯旋16668. 【啃书】《智能优化算法及其MATLAB实例》例4.3免疫算法求解TSP问题. CSDN博客.
[2] 曲怪曲怪. 智能算法之免疫算法求解TSP问题. CSDN博客.
[3] 杨震, 陈立万, 刘莎, 等. 基于免疫克隆多目标优化的WSN覆盖控制研究[J]. 电脑知识与技术, 2018, 14(28): 172-175+181.












![闵可夫斯基距离—大白话篇幅[有错误的话请指教]](https://img-blog.csdnimg.cn/20190624195707120.png)