递归实现前序遍历
二叉树的前序遍历是指从根节点出发,按照先根节点,再左子树,后右子树的方法遍历二叉树中的所有节点,使得每个节点都被访问一次。
当调用遍历算法的时候前序遍历的具体过程如下:
- 首先访问根节点,如果根节点不为空,执行输出语句,打印根节点的值。
- 如果左子树不为空,则访问根节点的左孩子,并输出根节点做孩子的值
- 继续访问根节点的左孩子的左孩子,如果不为空则继续输出该左孩子的值;
- 如果这时左孩子为空,说明该节点是叶子节点,则按照先左孩子后右孩子的访问方式访问其左右孩子,如果不为空就打印输出
- 左子树访问完毕之后,继续访问根节点的右子树,如果根节点的右孩子不为空,则输出该右孩子
- 继续访问根节点右孩子的左孩子,如果不为空,则输出
- 接着访问根节点右孩子的右孩子,如果不为空,则输出
可以发现这个过程是不断循环进行的,可以使用递归算法实现,具体代码如下:
// 前序遍历的递归实现public void preOrderTraverse(TreeNode node) {if (node == null)return;// 先根节点System.out.println(node.val);// 再左孩子preOrderTraverse(node.left);// 后右孩子preOrderTraverse(node.right);}为了测试使用,我构造一棵二叉树,先添加如下测试代码:
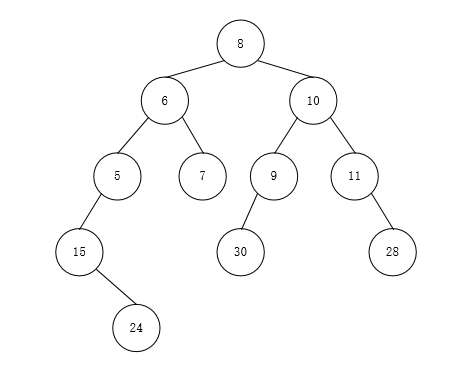
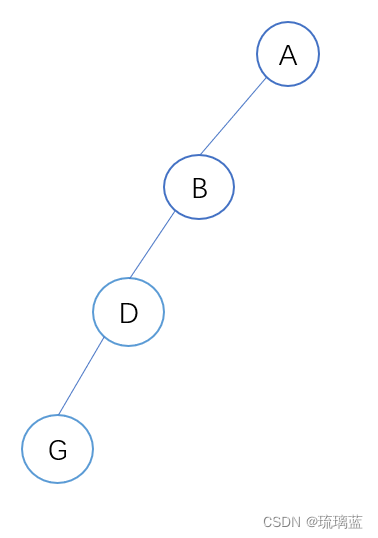
public static void main(String[] args) {TreeNode root = new TreeNode(8);TreeNode node1 = new TreeNode(6);TreeNode node2 = new TreeNode(10);TreeNode node3 = new TreeNode(5);TreeNode node4 = new TreeNode(7);TreeNode node5 = new TreeNode(9);TreeNode node6 = new TreeNode(11);TreeNode node7 = new TreeNode(15);TreeNode node8 = new TreeNode(24);TreeNode node9 = new TreeNode(30);TreeNode node10 = new TreeNode(28);root.left = node1;root.right = node2;node1.left = node3;node3.left = node7;node7.right = node8;node1.right = node4;node2.left = node5;node2.right = node6;node5.left = node9;node6.right = node10;TraverseTree t = new TraverseTree();t.preOrderTraverse(root);}构造出来的二叉树是这样的:
所以根据前面的前序遍历算法遍历的结果应该是:8,6,5,15,24,7,10,9,30,11,28。
非递归方式实现前序遍历

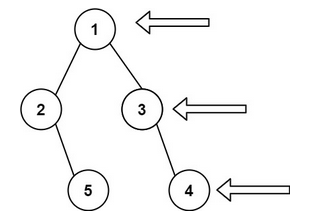
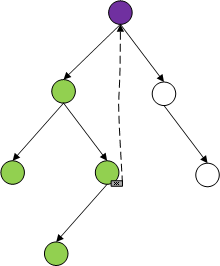
(图1) 前序遍历
(图2) 前序遍历访问3号结点时的栈状态
【思路】
1.对于前序遍历,每当访问一个结点时,先打印结点。
2.如果存在右子树,那么将右子树的根节点进行进栈保存,否则忽略。
3.如果存在左子树,那么将左子树的根节点进行进栈保存,然后弹出,将遍历引用指向左子树根节点,否则出栈回溯。
4.循环的退出条件是需要出栈操作时,栈为空,无法进行该操作。
【代码一】
import java.util.ArrayList;
import java.util.EmptyStackException;
import java.util.List;
import java.util.Stack;public class PreOrderTraversal {public static List<Integer> preOrderTraversal(TreeNode root) {Stack<TreeNode> stack = new Stack<TreeNode>();List<Integer> result = new ArrayList<Integer>();if (root == null) {return result;} else {TreeNode node = root;while (true) {result.add(node.val);if (node.right != null) {//左节点入栈stack.push(node.right);}if (node.left != null) {//右节点入栈,并弹出stack.push(node.left);node = stack.pop();} else {try {//左子节点没有,并且栈不空,就开始弹出保存的右子节点node = stack.pop();} catch (EmptyStackException e) {node = null;}}//栈空,并且没有左子树,结束循环if (node == null) {break;}}}return result;}
}
【代码二】递归代码很简洁,但是也有一些不是很好理解,能不能直接使用循环的方法加以解决呢?采用非递归的思路其实与上面是一致的,不过在遍历的过程中需要使用一些额外的空间保存遍历的中间结果,下面是使用非递归的方式实现前序遍历的代码:
// 前序遍历的非递归实现public void preOrderTraverse2(TreeNode node) {if (node == null) return;//创建一个栈用于保存遍历的结点Stack<TreeNode> s = new Stack<TreeNode>();while(node != null || !s.isEmpty()){//遍历左子树while(node != null){System.out.print(node.val + " ");s.push(node);node = node.left;}//遍历右子树if(!s.isEmpty()){node = s.pop();node = node.right;}}}