二叉树作为一种重要的数据结构,它的很多算法的思想在很多地方都用到了,比如STL算法模板,里面的优先队列、集合等等都用到了二叉树里面的思想,先从二叉树的遍历开始:
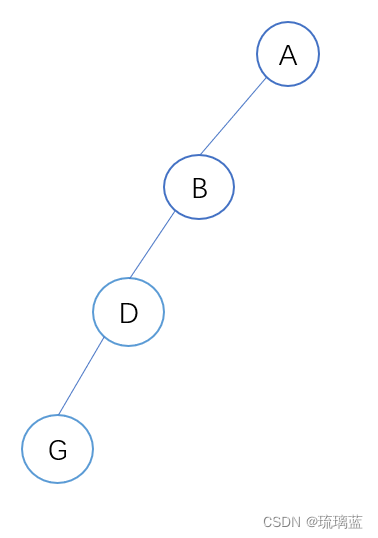
看二叉树长什么样子:
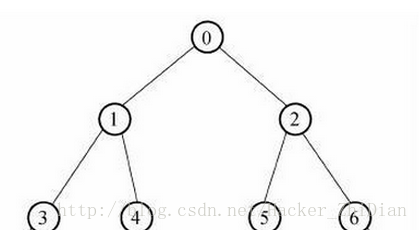
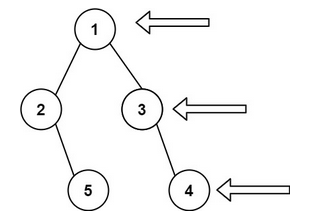
我们可以看到这颗二叉树一共有七个节点
0号节点是根节点
1号节点和2号节点是0号节点的子节点,1号节点为0号节点的左子节点,2号节点为0号节点的右子节点
同时1号节点和2号节点又是3号节点、四号节点和五号节点、6号节点的双亲节点
五号节点和6号节点没有子节点(子树),那么他们被称为‘叶子节点’
这就是一些基本的概念
二叉树的遍历
二叉树常用的遍历方式有:前序遍历、中序遍历、后序遍历、层序遍历四种遍历方式,不同的遍历算法,其思想略有不同,我们来看一下这四种遍历方法主要的算法思想:
1、先序遍历二叉树顺序:根节点 –> 左子树 –> 右子树,即先访问根节点,然后是左子树,最后是右子树。
上图中二叉树的前序遍历结果为:0 -> 1 -> 3 -> 4 -> 2 -> 5 -> 6
2、中序遍历二叉树顺序:左子树 –> 根节点 –> 右子树,即先访问左子树,然后是根节点,最后是右子树。
上图中二叉树的中序遍历结果为:3 -> 1 -> 4 -> 0 -> 5 -> 2 -> 6
3、后续遍历二叉树顺序:左子树 –> 右子树 –> 根节点,即先访问左子树,然后是右子树,最后是根节点。
上图中二叉树的后序遍历结果为:3 -> 4 -> 1 -> 5 -> 6 -> 2 -> 0
4、层序遍历二叉树顺序:从最顶层的节点开始,从左往右依次遍历,之后转到第二层,继续从左往右遍历,持续循环,直到所有节点都遍历完成
上图中二叉树的层序遍历结果为:0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 6
下面是四种算法的伪代码:
前序遍历:
preOrderParse(int n) {if(tree[n] == NULL)return ; // 如果这个节点不存在,那么结束 cout << tree[n].w ; // 输出当前节点内容 preOrderParse(tree[n].leftChild); // 递归输出左子树 preOrderParse(tree[n].rightChild); // 递归输出右子树
}中序遍历:
inOrderParse(int n) {if(tree[n] == NULL)return ; // 如果这个节点不存在,那么结束 inOrderParse(tree[n].leftChild); // 递归输出左子树 cout << tree[n].w ; // 输出当前节点内容 inOrderParse(tree[n].rightChild); // 递归输出右子树
}后序遍历:
pastOrderParse(int n) {if(tree[n] == NULL)return ; // 如果这个节点不存在,那么结束 pastOrderParse(tree[n].leftChild); // 递归输出左子树 pastOrderParse(tree[n].rightChild); // 递归输出右子树 cout << tree[n].w ; // 输出当前节点内容
}可以看到前三种遍历都是直接通过递归来完成,用递归遍历二叉树简答方便而且好理解,接下来层序遍历就需要动点脑筋了,我们如何将二叉树一层一层的遍历输出?其实在这里我们要借助一种数据结构来完成:队列。
我们都知道,队列是一种先进先出的数据结构,我们可以先将整颗二叉树的根节点加入队尾,然后循环出队,每次读取对头元素输出并且将队头元素出队,然后将这个输出的元素节点的的左右子树分别依次加入队尾,重复这个循环,知道队列为空的时候结束输出。那么整个二叉树就被我们采用层序遍历的思想输出来了。下面我们看一下上图的二叉树用层序遍历思想的遍历步骤:
对上面的步骤的伪代码实现
while(!que.empty()) {int n = que.front(); // 得到队头元素que.pop(); // 队头元素出队列 // 如果当前节点不为空,那么输出节点的数值,并且在队尾插入左右子节点if(tree[n] != NULL) {cout << tree[n].w;que.push(tree[n].leftChild); que.push(tree[n].rightChild); }
}这几个遍历算法的最终实现:
/** 二叉树的四种遍历方式,这里没有采用真实的指针去做,* 而是采用数组下标去模拟指针,是一种更加方便快速的方法 */
#include <iostream>
#include <queue>
using namespace std;
const int N = 10010;
const int INF = -1; // 我们用一个常数来表示当前二叉树节点为空的情况 struct Node {int w; // 当前树节点的值 int p; // 当前树节点的双亲所在数组下标 int l; // 当前树节点的左子节点所在数组下标 int r; // 当前树节点的右子节点所在数组下标
};
Node node[N];// 按照前序遍历二叉树的顺序输入树节点
void input(int n) {cin >> node[n].w;if(node[n].w == INF) { // 输入 -1 代表当前节点所在子二叉树停止输入 return ;}node[n].p = n / 2;node[n].l = n * 2;node[n].r = n * 2 + 1;input(n*2);input(n*2+1);
}// 前序遍历二叉树
void preOrderParse(int n) {if(node[n].w == INF) {return ;}cout << node[n].w << " ";preOrderParse(node[n].l);preOrderParse(node[n].r);
} // 中序遍历二叉树
void inOrderParse(int n) {if(node[n].w == INF) {return ;}inOrderParse(n*2);cout << node[n].w << " ";inOrderParse(n*2+1);
}// 后续遍历二叉树
void postOrderParse(int n) {if(node[n].w == INF) {return ;}postOrderParse(n*2);postOrderParse(n*2+1); cout << node[n].w << " ";
} /* * 层序遍历二叉树,这里采用的是 C++ STL 模板的提供的队列(queue),* 并没有自己去实现一个队列*/
void sequenceParse() {queue<int> que;int n = 1;que.push(1); // 插入根节点所在数组下标 while(!que.empty()) {n = que.front();que.pop(); // 得到队头元素并且将队头元素出队列 // 如果当前节点不为空,那么输出该节点,并且将该节点的左右子节点插入队尾 if(node[n].w != INF) { cout << node[n].w << " ";que.push(node[n].l);que.push(node[n].r);}}
}int main() {cout << "请以前序遍历的顺序输入二叉树,空节点输入 -1 :" << endl; input(1); // 从下标为 1 开始前序输入二叉树 cout << "前序遍历:" << endl; preOrderParse(1); cout << endl << "中序遍历:" << endl;inOrderParse(1);cout << endl << "后序遍历:" << endl;postOrderParse(1); cout << endl << "层序遍历:" << endl;sequenceParse();return 0;
}