目录
一、二叉树遍历算法的应用——二叉树的创建
二、二叉树遍历算法的应用——复制二叉树
三、二叉树遍历算法的应用——计算二叉树的深度
四、二叉树遍历算法的应用——计算二叉树节点总数
五、二叉树遍历算法的应用——计算二叉树叶子节点数
一、二叉树遍历算法的应用——二叉树的创建
1、按先序遍历序列建立二叉树的二叉链表
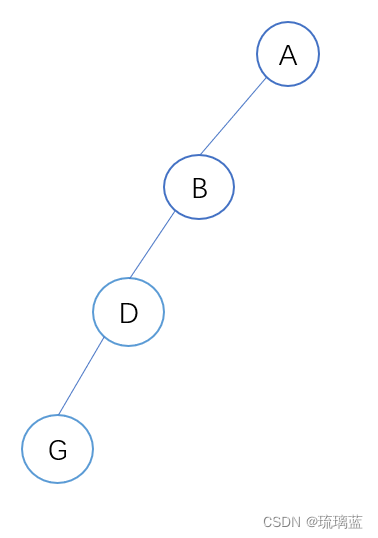
例如:已知先序序列为:ABCDEGF,按照二叉树先序方式建立可能会建立出两种不同的二叉树,如下图所示:

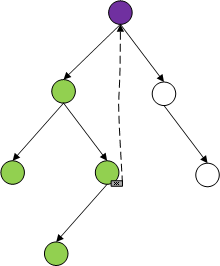
因此为了避免这种情况,我们可以补充一些空结点,补充空结点过后这两棵树接完全不一样了,因为补充的空结点的位置不一样。可用#号表示空结点。
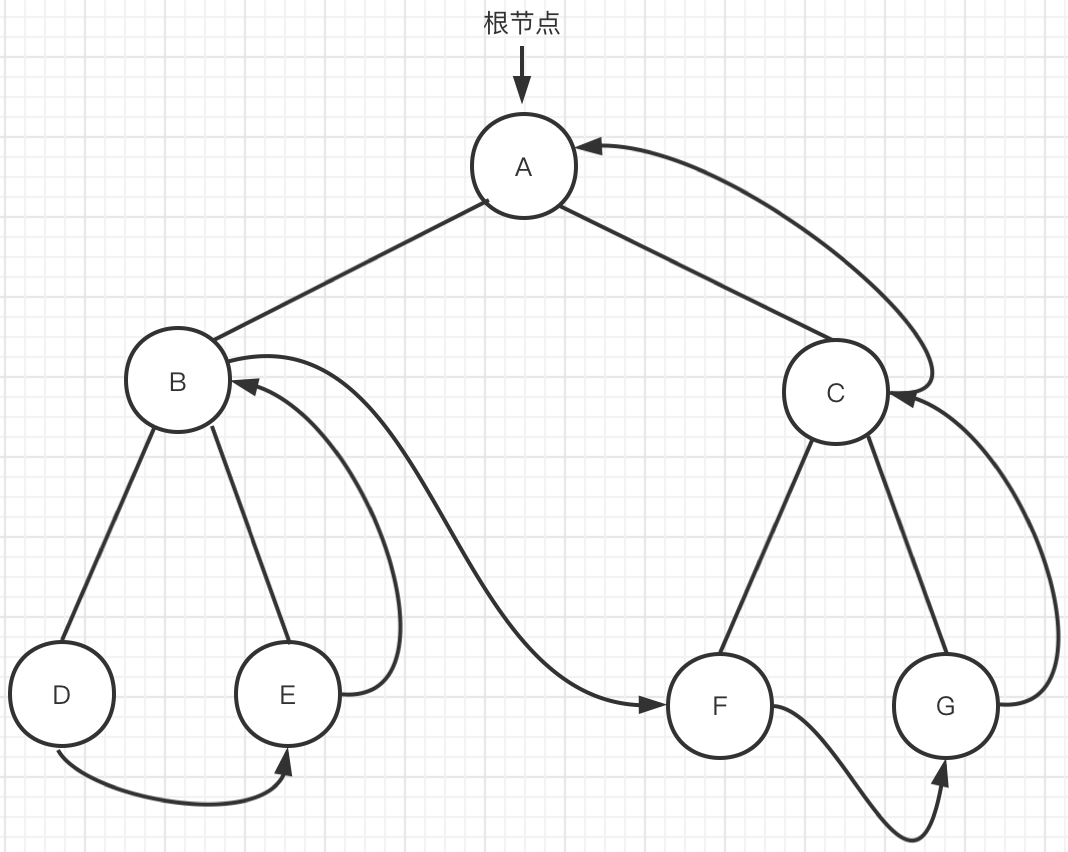
2、对下图所示二叉树按下列顺序读入字符:ABC##DE#G##F###

算法描述:
Status CreateBiTree(BiTree &T){scanf(&ch); //cin>>ch;if (ch== "#")T=NULL;else {if (!(T = (BiTNode *)malloc(sizeof(BiTNode)))) exit(OVERFLOW); //T=new BiTNode;T->data=ch; // 生成根结点CreateBiTree(T->lchild); //构造左子树
CreateBiTree(T->rchild); //构造右子树
}
return OK;}//CreateBiTree二、二叉树遍历算法的应用——复制二叉树
1、算法思路
如果是空树,递归结束;
否则,申请新结点空间,复制根结点
➢递归复制左子树
➢递归复制右子树
2、算法描述:
int Copy(BiTree T, BiTree &NewT){
if(T==NULL) { //如果是空树返回0
NewT=NULL; return 0;
}
else {NewT=new BiTNode;NewT->data=T->data;Copy(T->lChild, NewT->lchild);Copy(T->rChild, NewT->rchild);}}三、二叉树遍历算法的应用——计算二叉树的深度
1、算法思路
如果是空树,则深度为0; 否则,递归计算左子树的深度记为m,递归计算右子树的深度记为n,二叉树的深度则为m与n的较大者加1。
2、算法描述
int Depth( BiTree T){if(T==NULL) return 0; //如果是空树返回0
else {m=Depth(T->lChild);n=Depth(T->rChild);if(m>n)
return (m+1);else return(n+1);}
}四、二叉树遍历算法的应用——计算二叉树节点总数
1、算法思路
如果是空树,则结点个数为0;
否则,结点个数为左子树的结点个数+右子树的结点个数再+1。
2、算法描述
int NodeCount(BiTree T){if(T == NULL )return 0;elsereturn NodeCount(T-> lchild)+NodeCount(T->rchild)+ 1;}五、二叉树遍历算法的应用——计算二叉树叶子节点数
1、算法思路
如果是空树,则叶子结点个数为0;
否则,为左子树的叶子结点个数+右子树的叶子结点个数。
2、算法描述
int LeadCount(BiTree T){if(T==NULL) //如果是空树返回0return 0;if (T->Ichild==NULL && T->rchild == NULL)return 1; //如果是叶子结点返回1elsereturn LeafCount(T->Ichild)+LeafCount(T->rchild);}