二叉树遍历小结

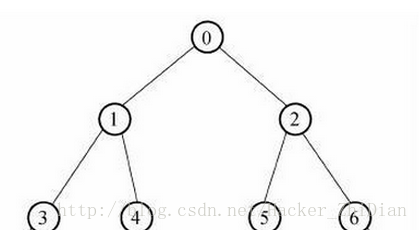
前言

二叉树是相当重要的数据结构，目前我还只会玩玩它的遍历（年轻不懂事没好好学，不然早就达到人生巅峰了），LeetCode上二叉树的简单题，大部分通过遍历加一点小逻辑即可解决，所以总结一下几种遍历方法（其实也是看题解白嫖的）。
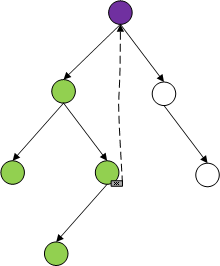
二叉树遍历有广度优先，深度优先两种方式，深度优先又分先序遍历（根，左，右），中序遍历（左，根，右），后序遍历(左，右，根)，如果是二叉搜索树，中序遍历就是有序的了。广度优先方式没太多说，只能借助队列实现，而深度优先，可通过递归方式，借助栈迭代方式，还有一种巧妙的莫里斯算法，空间复杂度是O(1)，但莫里斯算法应该会改变树的结构。

广度优先遍历

首先将根结点入队，然后只要队列非空，就出队一个元素，然后只要子节点不为空就入队，队列为空时，就是遍历完成时

public int bfs(TreeNode root) {Queue<TreeNode> queue=new LinkedList<TreeNode>();if(null!=root){queue.add(root);}int depth=0;while(!queue.isEmpty()){depth++;int size = queue.size();					//这两行不要也可以，按queue不为空就可以完成遍历for(int i=0;i<size;i++){					//size可以控制一层一次循环，可以获取当前的高度TreeNode curNode=queue.poll();if(null!=curNode.left){queue.add(curNode.left);}if(null!=curNode.right){queue.add(curNode.right);}}}return depth;
}

深度优先遍历

递归方式

递归方式代码很简洁，调整一下顺序前中后序遍历也都出来了。然后不断地嵌套函数调用，不管哪种语言每次函数调用操作系统都需要压栈，JVM中每次方法调用也是需要创建栈帧，如果数据量大会消耗大量内存，肯定会抛出StackOverflowError

1.先序
public void dfs(TreeNode root) {if(null==root){return;}System.out.println(root.val);dfs(root.left);dfs(root.right);
}2.中序
public void dfs(TreeNode root) {if(null==root){return;}dfs(root.left);System.out.println(root.val);dfs(root.right);
}
根右左遍历
public void dfs(TreeNode root) {if(null==root){return;}dfs(root.right);System.out.println(root.val);dfs(root.left);
}3.后序
public void dfs(TreeNode root) {if(null==root){return;}dfs(root.left);dfs(root.right);System.out.println(root.val);
}

迭代方式（先序）

深度优先先序迭代遍历，先将根节点入栈，然后只要栈非空，就出栈一个元素，这时需要将右子节点先入栈，左子节点后入栈，这样下一次循环出栈的是左子节点，再继续下去就达到了目的

public List<Integer> dfs(TreeNode root) {List<Integer> res=new LinkedList<>();if(null==root){return res;}Stack<TreeNode> stack = new Stack<>();stack.push(root);					//入栈根结点while(!stack.isEmpty()){TreeNode curNode=stack.pop();	//出栈最后加入结点res.add(curNode.val);if(null!=curNode.right){stack.push(curNode.right);	//先入栈右子结点，后出栈右结点}if(null!=curNode.left){stack.push(curNode.left);	//后入栈左子结点，先出栈左子结点}}return res;
}

迭代方式（中序）

深度优先中序迭代遍历，每次循环需要将根节点的所有左结点全部入栈，然后出栈最后一个左子结点，即第一个结点，如果该结点有右子结点，将根节点赋值为该右子结点，接着下一次循环，这样又会把右子树入栈，遍历完后会回到第一次循环的父节点，栈为空后达到目的

public List<Integer> dfs(TreeNode root) {List<Integer> res=new LinkedList<>();if(null==root){return res;}Stack<TreeNode> stack = new Stack<>();while(!stack.isEmpty()||null!=root){while(null!=root){				//如果左子结点不为空，一值入栈左子结点stack.push(root);root=root.left;}TreeNode curNode=stack.pop();	//弹出最后一个左子结点res.add(curNode.val);if(null!=curNode.right){root=curNode.right;			//右子结点不为空，先处理右字树}}return res;        
}

迭代方式（后序）

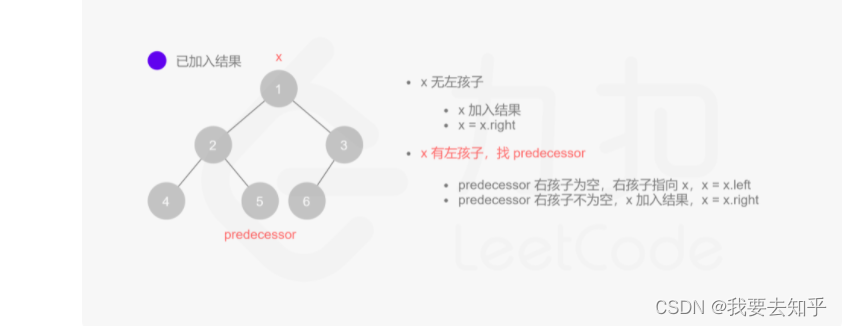
深度优先后序迭代遍历，每次循环需要将根节点的所有左结点全部入栈，然后出栈最后一个左子结点，如果存在右孩子，入栈当前节点，指针移到右孩子，进入下一轮循环，一样全部入栈左子结点，当右子结点为空，加入遍历结果集，这是将指针值为空并将前驱结点置为此节点（前驱结点就是用于处理有右孩子的结点），下一轮循环，如果结点的右孩子等于前驱结点，也可以加入结果，一直循环到栈为空指针为空，遍历完成

public List<Integer> dfs(TreeNode root) {List<Integer> res=new LinkedList<>();if(null==root){return res;}Stack<TreeNode> stack = new Stack<>();TreeNode pre=null;								//前驱结点TreeNode curNode=root;while(!stack.isEmpty()||null!=curNode){while(null!=curNode){						//左子结点一直入栈stack.push(curNode);curNode=curNode.left;}curNode=stack.pop();						//出栈最后结点if(null==curNode.right||curNode.right==pre){	//pre为有右子节点的结点的右结点，用于处理有右孩子的父结点res.add(curNode.val);pre=curNode;curNode=null;}else{							//如果右子结点不为空，入栈右子结点，下轮循环处理右字树stack.push(curNode);curNode=curNode.right;}}return res;
}

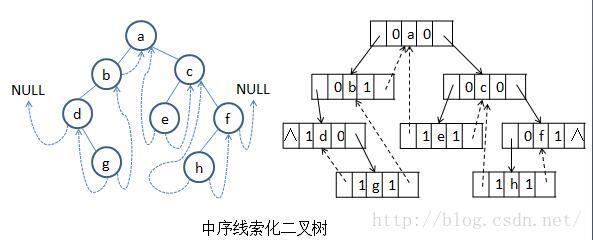
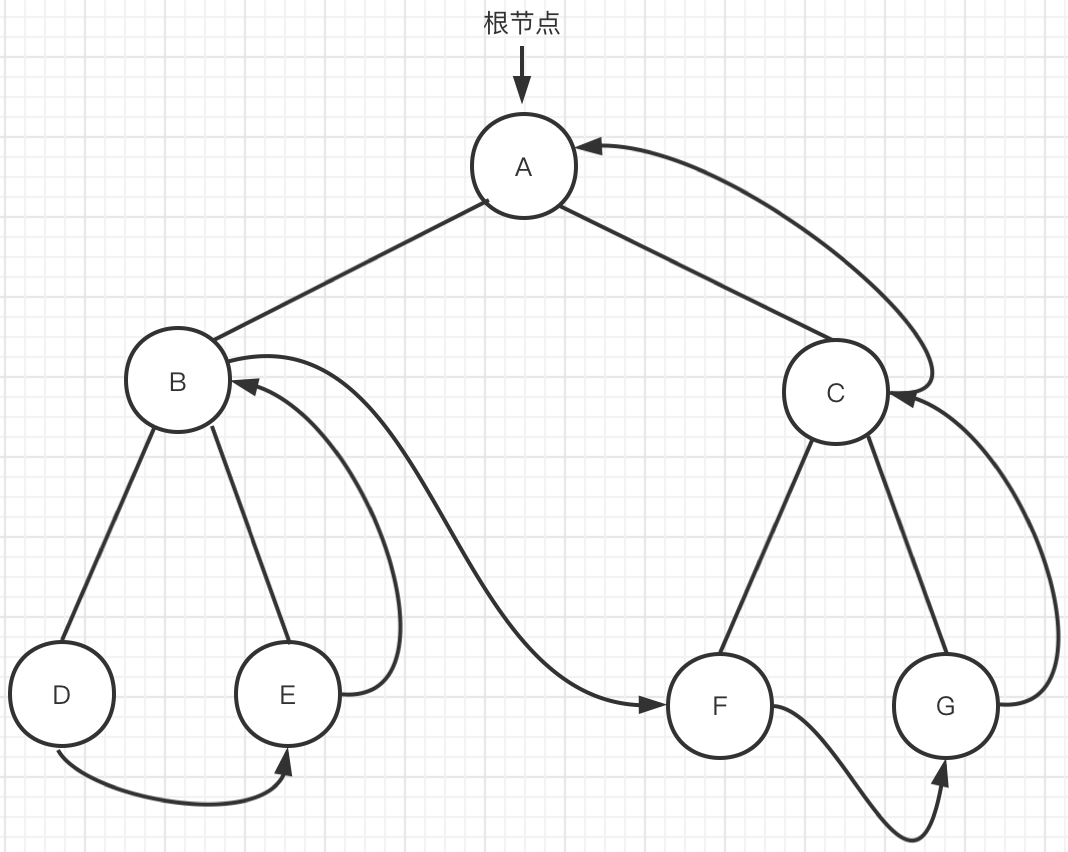
莫里斯算法

莫里斯算法用巧妙的方式，将迭代遍历的空间复杂度降低为O(1)，代码看起来没有多太多，但是理解却是需要更多的脑容量，这里借用了https://blog.csdn.net/yangfeisc/article/details/45673947的图解，有助于理解。

莫里斯先序

1 如果当前结点没有左子树，输出结点，当前结点指向右子结点，遍历右子树
2 如果当前结点有左子树，找到该左字树的最右子结点，如果最右子结点的右孩子为空，代表为根节点，输出结点值，如果最右子结点的右孩子不为空，当前移动到右孩子
3 当前结点为空，结束循环
莫里斯先序图解

public List<Integer> morris(TreeNode root) {List<Integer> res=new LinkedList<>();if(null==root){return res;}TreeNode cur = root;while(null!=cur){if(null==cur.left){					//用于处理最左子结点，最右子结点res.add(cur.val);cur=cur.right;					//回到后继根节点}else{TreeNode pre = cur.left;while(null!=pre.right&&pre.right!=cur){	 //找到左子结点的最右孩子，也就是根节点的前驱pre=pre.right;}if(null==pre.right){		//用于遍历其他结点，根节点,非最左最后res.add(cur.val);pre.right=cur;			//用于将前驱指向根节点	cur=cur.left;}else{					pre.right=null;cur=cur.right;				//用于回到根节点，或者移动到右子结点}}}return res;
}

莫里斯中序

1 如果当前结点没有左子树，输出结点，当前结点指向右子结点，遍历右子树
2 如果当前结点有左子树，找到该左字树的最右子结点，如果最右子结点不为空，代表为最左结点，输出结点值，然后回到父节点，或者右子结点
3 当前结点为空，结束循环
莫里斯中序图解

public List<Integer> morris(TreeNode root) {List<Integer> res=new LinkedList<>();if(null==root){return res;}TreeNode cur=root;while(null!=cur){if(null==cur.left){						//用于处理最左子结点,最右子结点res.add(cur.val);cur=cur.right;}else{TreeNode pre = cur.left;			//找到左子结点的最右孩子，即根节点的前驱结点while(null!=pre.right&&pre.right!=cur){pre=pre.right;}if(null==pre.right){				//用于将前驱指向根节点		pre.right=cur;cur=cur.left;}else{						res.add(cur.val);			//用于处理其他结点，左节点pre.right=null;cur=cur.right;				//用于回到根节点，或者移动到右子结点}}}return res;
}

莫里斯后序

莫里斯后序图解

public List<Integer> morris(TreeNode root) {List<Integer> res=new LinkedList<>();if(null==root){return res;}            TreeNode temp =new TreeNode();temp.left=root;TreeNode cur =temp;while(null!=cur){if(null==cur.left){// res.add(cur.val);				//最左子结点与最右子结点不再处理cur=cur.right;}else{TreeNode pre=cur.left;while(null!=pre.right&&pre.right!=cur){			//找到最右子结点，于根节点建立前驱联系pre=pre.right;}if(null==pre.right){pre.right=cur;								cur=cur.left;}else{pre.right=null;								//清掉前驱联系，重建二叉树TreeNode curTemp=cur.left;LinkedList<Integer> tempList=new LinkedList<>();		//处理所有结点，左子结点只处理一个，根节点与右子结点反向加入链表while(null!=curTemp){tempList.addFirst(curTemp.val);curTemp=curTemp.right;}res.addAll(tempList);						//后全部加入遍历集合cur=cur.right;}}}return res;
}