一、二叉树的定义
以字符串的形式定义一棵二叉树的先序序列,若字符是‘#’,表示该二叉树是空树,否则该字符是相应结点的数据元素。
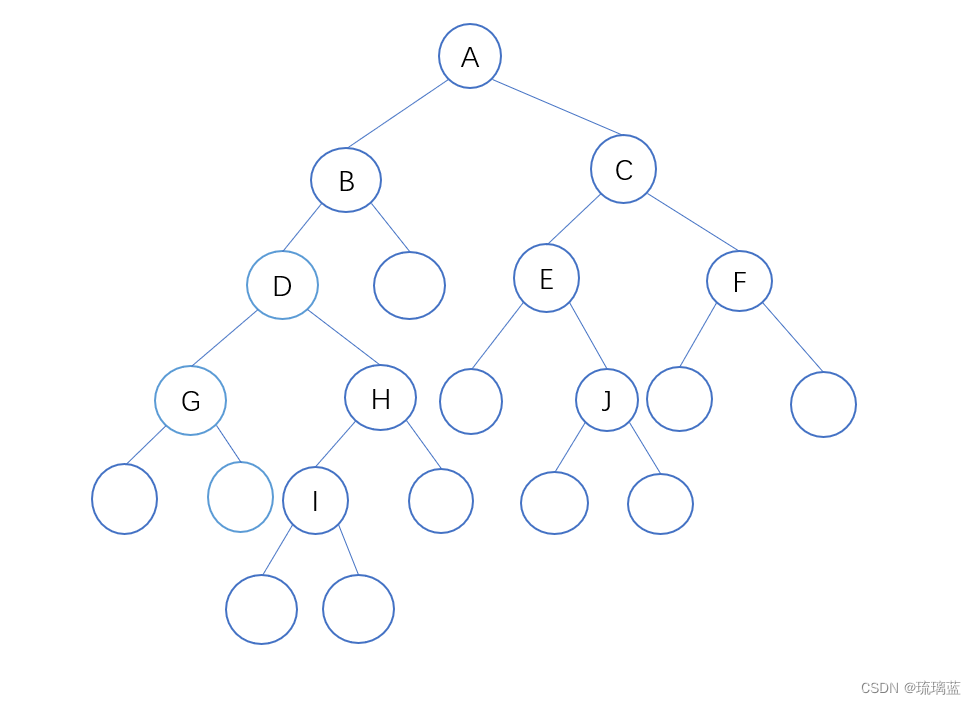
例:ABDG##HI####CE#J##F##
对应的二叉树:
思路讲解:
想要遍历二叉树,首先我们需要知道该二叉树是什么样子的,一般来说画出二叉树需要二叉树的先序序列+中序序列或者后序序列+中序序列,这里由于‘#’代表该二叉树是空树,让我们能够根据给出的先序序列画出二叉树。
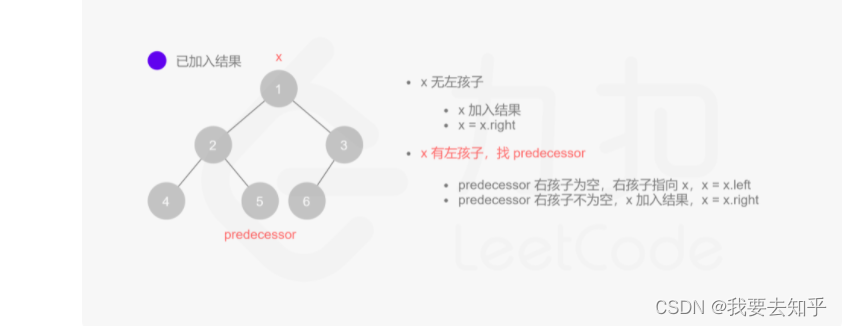
(1)我们知道二叉树的先序遍历是根左右的顺序,所以A为整个树的根结点,B为A的左子树。B后面是D,不是‘#’,说明B在该子树中为根结点,D为B的左子树,同理,G为D的左子树。此时的画出的树应该是这样的:
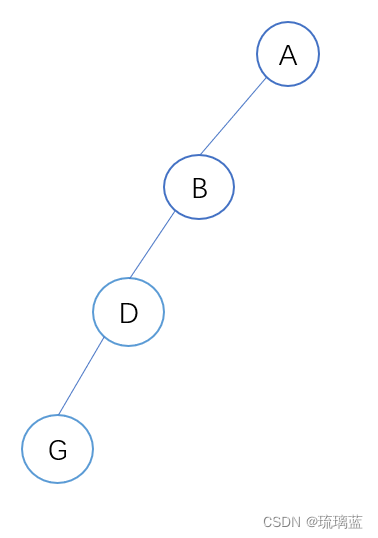
(2)接下来,G后面是‘#’,说明G没有左子树,这时已经遍历了G(根结点)以及它的左子树,由根左右的顺序,然后是它的右子树,下一个是‘#’,说明G既没有左子树,也没有右子树,为叶子结点。
(3)向上回溯,发现D没有遍历右子树,填入H即为D的右子树,H为该子树的根结点,填入I为H的左子树,I后面有两个‘#’,说明I为叶子结点。
重复(1)(2)(3)步骤,直到画出二叉树。
二、创建二叉树
1.定义结构体数组
const int max=10000;
struct tree
{char ch;int lch;int rch;
}datas[max];//这里直接定义了一个结构体数组,等价于struct tree datas[max]2.创建二叉树
#include<iostream>
using namespace std;const int maxnum=1000;//在create_tree函数中需要用到的变量。
char ch;
int count=0;//为结点进行编号struct tree
{char ch;int lch;int rch;
}datas[maxnum];int create_tree(int num)
{cin>>ch;if(ch=='#'){num=0;return num;}else{count++;num=count;datas[num].ch=ch;datas[num].lch=0;//初始化结点的左右子树datas[num].rch=0;datas[num].lch=create_tree(num);datas[num].rch=create_tree(num);}return num;
}
int main()
{int root=create_tree(0);return 0;
}三、遍历子树
1.先序遍历
先序遍历遵循根左右的顺序。
void preorder(int a)
{if(!a){return;}cout<<datas[a].ch;preorder(datas[a].lch);preorder(datas[a].rch);
}2.中序遍历
中序遍历遵循左根右的顺序。
void inorder(int a)
{if(!a){return;}inorder(datas[a].lch);cout<<datas[a].ch;inorder(datas[a].rch);
}3.后序遍历
后序遍历遵循左右根的顺序。
void postorder(int a)
{if(!a){return;}postorder(datas[a].lch);postorder(datas[a].rch);cout<<datas[a].ch;
}4.层次遍历
层次遍历可以使用队列结构(先进先出的特点)来完成算法。
1.初始化一个队列,根结点入队。
2.当队列非空时,循环执行下列步骤,否则遍历结束。
3.出队一个结点,并访问该结点。
4.若该结点的左子树非空,则左子树入队。
5.若该结点的右子树非空,则右子树入队。
void level_order(int x)
{char t;int s;queue<int> p;if(x)//if运行条件为x不等于0 {p.push(x);while(!p.empty()){s=p.front();p.pop();t=datas[s].ch;cout<<t;if(datas[s].lch!=0){p.push(datas[s].lch);}if(datas[s].rch!=0){p.push(datas[s].rch);}} }
}四、完整代码
#include<iostream>
#include<queue>
using namespace std;const int maxnum=1000;
char ch;
int count=0;struct tree
{char ch;int lch;int rch;
}datas[maxnum];int create_tree(int num)
{cin>>ch;if(ch=='#'){num=0;return num;}else{count++;num=count;datas[num].ch=ch;datas[num].lch=0;datas[num].rch=0;datas[num].lch=create_tree(num);datas[num].rch=create_tree(num);}return num;
}void preorder(int a)
{if(!a){return;}cout<<datas[a].ch;preorder(datas[a].lch);preorder(datas[a].rch);
}void inorder(int a)
{if(!a){return;}inorder(datas[a].lch);cout<<datas[a].ch;inorder(datas[a].rch);
}void postorder(int a)
{if(!a){return;}postorder(datas[a].lch);postorder(datas[a].rch);cout<<datas[a].ch;
}void level_order(int x)
{char t;int s;queue<int> p;if(x)//if运行条件为x不等于0 {p.push(x);while(!p.empty()){s=p.front();p.pop();t=datas[s].ch;cout<<t;if(datas[s].lch!=0){p.push(datas[s].lch);}if(datas[s].rch!=0){p.push(datas[s].rch);}} }
}int main()
{int root=create_tree(0);cout<<"二叉树的先序遍历序列:"<<endl;preorder(root);cout<<endl;cout<<"二叉树的中序遍历序列:"<<endl;inorder(root);cout<<endl;cout<<"二叉树的后序遍历序列:"<<endl;postorder(root);cout<<endl;cout<<"二叉树的层序遍历序列:"<<endl;level_order(root); return 0;
}