二叉树遍历算法

article/2025/10/8 18:01:30

目录

先序遍历

中序遍历

后序遍历

层序遍历

938. 二叉搜索树的范围和

110. 平衡二叉树

114. 二叉树展开为链表

117. 填充每个节点的下一个右侧节点指针 II

116. 填充每个节点的下一个右侧节点指针

1，三种遍历都是先把二叉树的最左结点循环入栈(DFS迭代)，以帮助找到返回处理的节点。

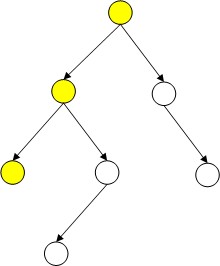
每个子树也是先把该右子树中的最左节点循环入栈，以帮助找到返回处理的节点。

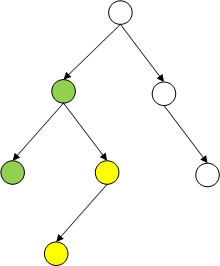
先序遍历和中序遍历都是通过一个左子树（全绿的）的最右下叶节点的right(灰NULL)带出接下来的处理结点（左子树的父结点（紫）），表明该处理结点的左子树已经遍历处理完毕。因为不管先序遍历还是中序遍历，一颗子树的结束点是在该子树的最右下叶节点。

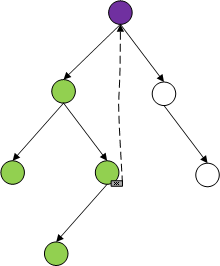
2，先序和中序代码结构一致，是处理完父和左或左和父之后再处理右，天然可以通过父节点带出右子树。但是后序遍历是先处理左和右再处理父，其中某次父节点出栈，只用一个栈的话没法确定左右是否处理完毕，因此需要增加一个栈记录状态。

3，后序遍历需要用两个栈，一个栈用于记录返回处理的结点，一个用于记录状态，0表示处理了左子结点，1表示处理了右子结点。

注：

1，二叉树遍历非递归经典解法DFS(栈)、BFS(队列)，注意入栈的条件都是当节点非空node != nullptr时入栈，否则从栈中取出节点指针，取值会非法。

2，DFS栈解法比递归的好处：以先序为例，在把当前p的right、left入栈后，在下一轮从栈pop出left前的这段时间，可以额外进行各种处理(如二叉树转为链表时需对p的left和right重置值leetcode114栈解法)，因为在额外处理前已经用栈记录了先序遍历的节点顺序。

先序遍历

DFS递归：

注：(递归:从上到下)先父节点，后子节点，是尾递归。

public void preorderTraversal(TreeNode node)
{if (node == null) {return;}System.out.println(node.value); // 访问当前结点preorderTraversal(node.left); // 前序遍历其左子树preorderTraversal(node.right); // 前序遍历其右子树
}

DFS栈解法1：DFS栈通用模板（只适用于先序遍历，因为只有先序遍历是先父后子）：CSDN

注：1，因为二叉树状态转换虽然是DAG(有向无环图)但不同路径间没有重复(从同一点A出发，只有一条路径到达另一点B)，所以左右孩子入栈前不需要(空间换时间的visit)判重。

       2，入栈栈顺序是先right孩子，后left孩子，这样出栈是先左后右，满足先序遍历顺序。

class Solution {
public:vector<int> preorderTraversal(TreeNode *root) {vector<int> result;stack<const TreeNode *> s;if (root != nullptr)s.push(root);while (!s.empty()) {const TreeNode *p = s.top();s.pop();result.push_back(p->val);if (p->right != nullptr) {s.push(p->right);}if (p->left != nullptr) {s.push(p->left);}}return result;}
};

DFS栈解法2：用栈stack记住来时的路（来时的路即父节点）

注：本解法的意图强调：用栈stack记住来时的路（即stack中是存的所有的父节点）。

//先序遍历（栈）
void pre_visit(BTree* root)
{std::stack<BTree*> stack_tree;BTree* cur_node = root;while(cur_node != NULL || !stack_tree.empty()){if(cur_node != NULL) { // 当前节点非空：记录到结果集，并入栈作为子节点的灯塔std::cout << cur_node->value.c_str() << "\t";  // 记录到结果集stack_tree.push(cur_node);  // 当前节点入栈cur_node = cur_node->leftChild;  // 处理左} else {cur_node = stack_tree.top();  // 父节点出栈stack_tree.pop();  //栈顶元素出栈cur_node = cur_node->rightChild;  // 处理右}}
}

中序遍历

DFS递归

注：先孩子，又父亲，再孩子。所以是非尾递归。

public void inorderTraversal(TreeNode node)
{if (node == null) {return;}inorderTraversal(node.left); // 中序遍历结点的左子树System.out.println(node); // 访问当前结点inorderTraversal(node.right); // 中序遍历结点的右子树
}

DFS栈：记住来时的路

//中序遍历（非递归）
void mid_visit(BTree* root)
{std::stack<BTree*> stack_tree; BTree* cur_node = root;while(cur_node != NULL || !stack_tree.empty()){if(cur_node != NULL) {stack_tree.push(cur_node);  //当前节点入栈cur_node = cur_node->leftChild;  //指向左子节点，进行相同处理} else {cur_node = stack_tree.top();  //指向栈顶节点stack_tree.pop();  //栈顶节点出栈std::cout << cur_node->value.c_str() << "\t";  //处理当前节点的值cur_node = cur_node->rightChild;  //指向右子节点，进行相同处理}}
}

后序遍历

DFS递归（非尾递归）

public void postorderTraversal(TreeNode node) {if (node == null) {return;}postorderTraversal(node.left); // 后序遍历结点的左子树postorderTraversal(node.right); // 后序遍历结点的右子树System.out.println(node); // 访问当前结点
}

 DFS栈：

思路1：借用先序遍历的"根左右"入结果集。改为"根右左"入一个可以支撑倒序的容器，并反向输出得到"左右根"

思路1-解法1：以"根右左"顺序插入list头记录结果，转为vector输出, 用dfs栈通用模板实现.

前序遍历顺序为：根 -> 左 -> 右，后序遍历顺序为：左 -> 右 -> 根
如果1： 我们将前序遍历中结点插入结果链表尾部的逻辑，修改为将结点插入结果链表的头部
那么结果链表就变为了：右 -> 左 -> 根
如果2： 我们将遍历的顺序由从左到右修改为从右到左，配合如果1
那么结果链表就变为了：左 -> 右 -> 根，与后序遍历要求的顺序一致
所以可以按如下步骤实现：
1. 修改前序遍历代码中，结点写入结果链表的代码，将插入队尾修改为插入队首
2. 修改前序遍历代码中，每次先查看左结点再查看右结点的逻辑，变为先查看右结点再查看左结点

中间结果记录在一个list里面，处理完了后再转为vector返回。

    vector<int> postorderTraversal(TreeNode* root){list<int> result;// 结果集stack<TreeNode*> stk;if (root != nullptr)stk.push(root);while (!stk.empty()) {const TreeNode *p = stk.top();stk.pop();result.push_front(p->val); // 插入list头if (p->left != nullptr) {stk.push(p->left);}if (p->right != nullptr) {stk.push(p->right);}}return vector<int>(result.begin(), result.end());}

思路1-解法2 以"根右左"顺序插入list头记录结果，转为vector输出。用栈stack记住来时的路模板实现。

vector<int> postorderTraversal(TreeNode* root)
{list<int> result; // 结果集stack<TreeNode*> stk;TreeNode* node = root;while (node != nullptr || !stk.empty()) {if (node != nullptr) {// 对应处理1，每次遍历时，都将结点写入结果链表头，而不是尾result.push_front(node->val);stk.push(node);// 对应处理2，每次先遍历右结点，再遍历左结点node = node->right;} else {node = stk.top();stk.pop();// 对应处理2，每次先遍历右结点，再遍历左结点node = node->left;}}return vector<int>(result.begin(), result.end());
}

思路1-解法3 以"根右左"顺序入stack2(双栈)，stack2弹出元素到vector输出。用dfs栈通用模板实现.

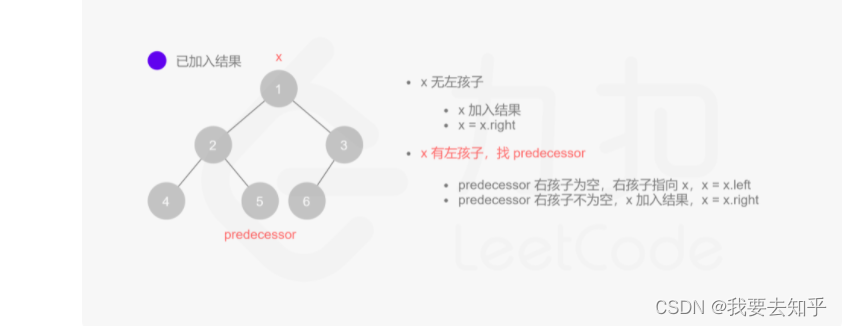
    vector<int> postorderTraversal3(TreeNode* root){vector<int> res;stack<TreeNode*> stk1;stack<TreeNode*> stk2;if (root != nullptr) {stk1.push(root);}while (!stk1.empty()) {TreeNode *node = stk1.top();stk1.pop();stk2.push(node);if (node->left != nullptr) {stk1.push(node->left);}if (node->right != nullptr) {stk1.push(node->right);}}while (!stk2.empty()) {TreeNode *node = stk2.top();stk2.pop();res.push_back(node->val);}return res;}

思路1-解法4 (双100%， 0ms, 8.6MB)(适用于前序、中序、后序)： 要求的遍历序"左右根" 入vector，倒序1为“根右左”，“根右左”入stack（会再倒序2出栈为“左右根”）。其中(1)每个“左右根”三节点入vector时需要用根的val值构造出一个新根(左右孩子为nullptr)入vector的，这样保证在dfs栈通用模板循环中用左右孩子为nullptr来取到target。(2)dfs通用模板内层循环不是cur的neighbers入栈，而是vector倒序号的“根右左”通通入栈。用dfs栈通用模板实现。

先把根结点入栈，随后每次从栈顶取出一个，它是我们当前遍历到的结点。(1)构造一个值与u的值相同的叶子结点u'，并与 u 的所有子结点一起，按遍历要求的次序(即正常序的前、中后序)，(2)逆序推入栈中. (3)利用栈的逆序性，从栈中取出时又是第(1)步中的正常序。例如 u 的子结点从左到右为v1, v2, 如果是前序遍历（根--左--右），那么推入栈的顺序应当为v2, v1, u'，如果是中序遍历，则是v2, u',v1，后序遍历则是u',v2,v1。这样就保证了下一个遍历到的结点出现在栈顶的位置。这样，遍历栈，每次取出栈顶元素后，只要判断当前结点是否是叶子结点。如果是叶结点，直接输出到结果集，继续取下一个元素；如果不是叶结点，就把当前结点替换成同值叶结点，逆序入栈即可。

注：这种方法遍历一遍，stk中存的是一颗新树，每个节点的left, right都是nullptr(相当于每个节点都是叶)，都是把原始树中的对应节点的值后new出来的新节点，原始树没有改变。

    enum OrderType {PREORDER,INORDER,POSTORDER,};vector<int> postorderTraversal(TreeNode* root) {return traversal(root, POSTORDER);}vector<int> traversal(TreeNode* root, OrderType orderType){if (root == nullptr) {return {};}vector<int> result;stack<TreeNode*> stk;stk.push(root);while (!stk.empty()) {TreeNode* node = stk.top();stk.pop();// 叶结点直接加入结果集if (node->left == nullptr && node->right == nullptr) {result.push_back(node->val);continue;}// 按次序入栈vector<TreeNode*> eachNodeFamily;eachNodeFamily = OrderNodes(orderType, node);for (auto ele : eachNodeFamily) {stk.push(ele);}}return result;}vector<TreeNode*> OrderNodes(OrderType orderType, TreeNode* node){vector<TreeNode*> nodes;TreeNode* tmp = new TreeNode(node->val); // 当前结点替换成同值叶结点switch (orderType) {case PREORDER: // 根--左--右nodes.push_back(tmp);if (node->left != nullptr) nodes.push_back(node->left);if (node->right != nullptr) nodes.push_back(node->right);break;case INORDER: // 左--根--右if (node->left != nullptr) nodes.push_back(node->left);nodes.push_back(tmp);if (node->right != nullptr) nodes.push_back(node->right);break;case POSTORDER: // 左--右--根if (node->left != nullptr) nodes.push_back(node->left);if (node->right != nullptr) nodes.push_back(node->right);nodes.push_back(tmp);break;}reverse(nodes.begin(), nodes.end()); // 逆序后入栈保证取出来的次序正确return nodes;}

思路2：

后序遍历需要用两个栈，一个栈用于记录返回处理的结点，一个用于记录状态，0表示处理了左子结点，1表示处理了右子结点。

//后序遍历（非递归）
void post_visit(BTree* root)
{std::stack<BTree*> stack_tree;  //保存需要返回处理的节点std::stack<int> stack_flag;  //保存返回的路径标识BTree* cur_node = root;while(cur_node != NULL || !stack_tree.empty()){if(cur_node != NULL) {stack_tree.push(cur_node);  //当前节点入栈stack_flag.push(0);  //下一步处理leftChild，返回时从leftChild返回，保存标识为0cur_node = cur_node->leftChild;  //指向leftChild，进行步骤1处理} else {cur_node = stack_tree.top();  //指向栈顶元素stack_tree.pop();  //节点出栈int flag = stack_flag.top();  //获取返回路径stack_flag.pop();  //标识出栈if(flag == 0) {//从leftChild返回，此时应该处理rightChildstack_tree.push(cur_node);  //当前节点入栈stack_flag.push(1);  //下一步处理rightChild，保存标识1cur_node = cur_node->rightChild;  //指向rightChild，进行步骤1处理} else {//从rightChild返回，此时应该处理根节点的值std::cout << cur_node->value.c_str() << "\t";  //处理根节点的值cur_node = NULL;  //为了进行步骤2，根据循环逻辑，这里要将cur_node置空}}}
}

层序遍历

题目（leetcode102）

思路1-解法1：单队列 + 每层的计数，队列作为外层循环，一层的计数作为内存循环条件. BFS通用模板.

    vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*> q;vector<vector<int>> res;if (root == NULL) {return res;}q.push(root);while (!q.empty()) {vector<int> this_level_vec;int size = q.size();for (int i = 0; i < size; i++) {// this level node dequeue, and keep recode by vecTreeNode * t = q.front();q.pop();this_level_vec.push_back(t->val);// next level node enqueueif (t->left != nullptr) {q.push(t->left);}if (t->right != nullptr) {q.push(t->right);}}res.push_back(this_level_vec);}return res;}

思路1：每层的数据以一个vector记录下来后再放到结果vector中。

思路1-解法2：双队列，cur作为内外层循环条件, 内存循环时cur队列取下一层节点存放next队列, 两队列swap. BFS通用模板.

    vector<vector<int>> levelOrder(TreeNode *root){queue<TreeNode *> cur;queue<TreeNode *> next;vector<vector<int>> res;if (root != nullptr) {cur.push(root);}while (!cur.empty()) {vector<int> levRes;while (!cur.empty()) {TreeNode *node = cur.front();cur.pop();levRes.push_back(node->val);if (node->left != nullptr) {next.push(node->left);}if (node->right != nullptr) {next.push(node->right);}}res.push_back(levRes);cur.swap(next); // 若类没有自己的swap成员方法, 则用标准库函数swap(cur, next);}return res;}

思路2：用level作为idx精确记录第几层。DFS递归通用模板（也是尾递归） 

class Solution {
public:vector<vector<int> > levelOrder(TreeNode *root){vector<vector<int>> result;traverse(root, 1, result);return result;}void traverse(TreeNode *root, size_t level, vector<vector<int>> &result){if (!root) return;// 每层建立空数组if (level > result.size()) {result.push_back(vector<int>());}// 利用level精确记录第level层的元素，入参level一定要是传值，不能传引用result[level - 1].push_back(root->val);traverse(root->left, level + 1, result);traverse(root->right, level + 1, result);}
};

练习：

938. 二叉搜索树的范围和

//思路：法1：中序遍历，遍历节点元素值放入vector，对vector用泛型算法计算范围和。

法2：中序遍历 + 一个结果值在满足条件时累加。

法3：dfs递归根据条件剪枝(结合二叉搜索树的特性)。DFS递归(先序、中序、后序都可以)。我们对树进行dfs递归，对于当前节点 node，如果 node.val 小于等于 L，那么只需要继续搜索它的右子树；如果 node.val 大于等于 R，那么只需要继续搜索它的左子树；如果 node.val 在区间 (L, R) 中，则需要搜索它的所有子树。本方法的两种解法（从下到上--有return 值和从上到下--传参sum）配合剪枝时的return技巧，很有代表性。

    //根据三种方法：总结，二叉搜索树的求满足比较大小条件的遍历，要能想到方法3，根据条件遍历某分支即可，剪枝。// 法1：中序遍历存入vector，取L、R两值之间元素和。int rangeSumBST1(TreeNode* root, int L, int R) {vector<int> inOrderVec;InOrderTravel(root, inOrderVec);auto leftIt = find(inOrderVec.begin(), inOrderVec.end(), L);auto rightIt = find(inOrderVec.begin(), inOrderVec.end(), R);return accumulate(leftIt, rightIt, 0) + *rightIt;}// 224msvoid InOrderTravel(TreeNode* root, vector<int>& inOrderVec){if (root != nullptr) {InOrderTravel(root->left, inOrderVec);inOrderVec.push_back(root->val);InOrderTravel(root->right, inOrderVec);}}// 288msvoid InOrderTravel1(TreeNode* root, vector<int>& inOrderVec){stack<TreeNode*> stk;while (root != nullptr || !stk.empty()) {if (root != nullptr) {stk.push(root);root = root->left;} else {TreeNode* node = stk.top();stk.pop();inOrderVec.push_back(node->val);root = node->right;}}}//法2：仍然中序(没必要中序)，但不用把所有元素记录到vector. 直接根据L/R累加记录到结果。int rangeSumBST2(TreeNode* root, int L, int R) {int sum= 0;InOrderTravel(root, sum, L, R);return sum;}// 252msvoid InOrderTravel2(TreeNode* root, int& sum, int L, int R){if (root != nullptr) {InOrderTravel2(root->left, sum, L, R);if (L <= root->val && root->val <= R) {sum += root->val;}InOrderTravel2(root->right, sum, L, R);}}//法3：DFS递归(这里用后序).//我们对树进行深度优先搜索，对于当前节点 node，如果 node.val 小于等于 L，//那么只需要继续搜索它的右子树；如果 node.val 大于等于 R，那么只需要继续搜索它的左子树；//如果 node.val 在区间 (L, R) 中，则需要搜索它的所有子树。
解法1： 从下到上，递归函数有返回值。注意配合剪枝的return技巧。int rangeSumBST(TreeNode *root, int low, int high) {if (root == nullptr) {return 0;}if (root->val > high) { // 仅剪枝，并返回，因为不在给定范围内所以不累加return rangeSumBST(root->left, low, high);}if (root->val < low) { // 仅剪枝，并返回，因为不在给定范围内所以不累加return rangeSumBST(root->right, low, high);}// 这里本结点值在给定范围内，从下到上递归，根据后续节点值，累加上本结点值，并返回。return root->val + rangeSumBST(root->left, low, high) + rangeSumBST(root->right, low, high);}解法2：从上到下（尾递归），递归函数无返回值，传sum引用累加结果。注意配合剪枝的技巧。int rangeSumBST(TreeNode* root, int L, int R) {int sum= 0;PreOrderTravel(root, sum, L, R);return sum;}// 212ms 从上到下（尾递归），递归函数无返回值，传sum引用累加结果。void PreOrderTravel(TreeNode* root, int& sum, int L, int R){if (root != nullptr) {if (L <= root->val && root->val <= R) {sum += root->val;}if (root->val > L) {PreOrderTravel(root->left, sum, L, R);}if (root->val < R) {PreOrderTravel(root->right, sum, L, R);}}}// dfs递归后序：int rangeSumBST(TreeNode* root, int L, int R) {int sum = 0;PostCondDfs(root, L, R, sum);return sum;}// 从下到上，递归函数无返回值，传sum引用累加结果。void PostCondDfs(TreeNode *root, int L, int R, int &sum){if (root == nullptr) {return;}if (root->val > L) {PostCondDfs(root->left, L, R, sum);}if (root->val < R) {PostCondDfs(root->right, L, R, sum);}if (L <= root->val && root->val <= R) {sum += root->val;}}

110. 平衡二叉树

思路：

// (1) dfs递归:从下到上(逆向dfs), 先子, 后父. 非尾递归

// (2) 题目是判断型(不满足条件时要恒定return返回一个特殊值) + 结果型(return返回二叉树的高)

// (3) 需要判断型的return返回先于结果型的return返回

    bool isBalanced(TreeNode* root) {return BalancedHeight(root) >= 0;}int BalancedHeight(TreeNode* root) {if ( root == nullptr) {return 0;}int left = BalancedHeight(root->left);int right = BalancedHeight(root->right);if (left < 0 || right < 0 || abs(left - right) > 1) {return -1;}return max(left, right) + 1;}

114. 二叉树展开为链表

     思路1: 前序遍历(三种方法都可以)放入vector, 遍历vector把各元素left置null, right指向下一个TreeNode 

    // 代码略.

    思路2：前序遍历的过程中, 各TreeNode的left置为null, right指向先序遍历下一节点(处于当前栈顶位置)。只能用dfs栈通用模板, 只有这个解法才能使得先记录下一节点(即右节点)到栈, 再记录前一节点(即左节点)入栈.

    void flatten(TreeNode* root) {if (root == nullptr) {return;}stack<TreeNode*> stk;stk.push(root);while (!stk.empty()) {TreeNode* node = stk.top();stk.pop();if (node->right != nullptr) {stk.push(node->right);}if (node->left != nullptr) {stk.push(node->left);}node->left = nullptr;if (!stk.empty()) {node->right = stk.top();}}}

法1法2都用到了栈, 递归的调用栈也是栈。都是O(n) O(n)的，为了得到O(n) O(1)

思路3：官网解答方法3

注意到前序遍历访问各节点的顺序是根节点、左子树、右子树。如果一个节点的左子节点为空，则该节点不需要进行展开操作。如果一个节点的左子节点不为空，则该节点的左子树中的最后一个节点被访问之后，该节点的右子节点被访问。该节点的左子树中最后一个被访问的节点是左子树中的最右边的节点，也是该节点的前驱节点。因此，问题转化成寻找当前节点的前驱节点。

具体做法是，对于当前节点，如果其左子节点不为空，则在其左子树中找到最右边的节点，作为前驱节点，将当前节点的右子节点赋给前驱节点的右子节点，然后将当前节点的左子节点赋给当前节点的右子节点，并将当前节点的左子节点设为空。对当前节点处理结束后，继续处理链表中的下一个节点，直到所有节点都处理结束。

    void flatten3(TreeNode* root) {TreeNode *curr = root;while (curr != nullptr) {if (curr->left != nullptr) {auto next = curr->left;auto pre = next;while (pre->right != nullptr) {pre = pre->right;}pre->right = curr->right;curr->left = nullptr;curr->right = next;}curr = curr->right;}}

117. 填充每个节点的下一个右侧节点指针 II

思路：dfs递归模板

（1）传参时直接把参数1的需要的next作为参数2传入

（2）提前从cur相同的层遍历找出cur孩子节点的sibling. cur孩子节点的sibling要么是父节点的right，要么是上层有效next的left或right

（3）先遍历右孩子，保证上层所有节点的next可以从右往左建立完整

    Node* connect(Node* root) {ConnectDfs(root, nullptr);return root;}void ConnectDfs(Node *cur, Node *slibing){if (cur == nullptr) {return;}cur->next = slibing;// 需要提前从cur相同的层遍历找出cur孩子节点的siblingNode *childSibling = nullptr; // 孩子节点的siblingNode *curValidNextNode = cur->next; // 在当前层上遍历对cur的child的有效节点while (curValidNextNode != nullptr) {if (curValidNextNode->left != nullptr || curValidNextNode->right != nullptr) {childSibling = curValidNextNode->left != nullptr ? curValidNextNode->left : curValidNextNode->right;break;}curValidNextNode = curValidNextNode->next;}ConnectDfs(cur->right, childSibling);ConnectDfs(cur->left, cur->right != nullptr ? cur->right : childSibling);}

116. 填充每个节点的下一个右侧节点指针

思路：

因为是完美二叉树，所以孩子节点的sibling是确定的。所有的left的sibling都为right, right的sibling要么是父节点sibling的left要么是nullptr。不再需要单独在父节点层遍历得到，也不需要先遍历右孩子再遍历左孩子。

    void connect(Node* root, Node* sibling){if (root == nullptr) {return;}root->next = sibling;connect(root->left, root->right);if (sibling != nullptr) {connect(root->right, sibling->left);} else {connect(root->right, nullptr);}}


http://chatgpt.dhexx.cn/article/Cm4bkodA.shtml

相关文章

二叉树的四种遍历算法（结构体数组）

二叉树的四种遍历算法（结构体数组）

一、二叉树的定义 以字符串的形式定义一棵二叉树的先序序列&#xff0c;若字符是‘#’&#xff0c;表示该二叉树是空树&#xff0c;否则该字符是相应结点的数据元素。 例&#xff1a;ABDG##HI####CE#J##F## 对应的二叉树&#xff1a; 思路讲解&#xff1a; 想要遍历二叉树&am…
阅读更多...
二叉树的四种遍历方式

二叉树的四种遍历方式

概要 树本身是一种简单化的图 &#xff1b; DFS对应前中后序遍历&#xff0c;BFS对应层序遍历 二叉树结构 struct treenode {int val;treenode *left;treenode *right;treenode() : val(0), left(nullptr), right(nullptr) {}treenode(int x) : val(x), left(nullptr), right(n…
阅读更多...
针对Linux学习，值得阅读的五本书籍，不看可能错失机会

针对Linux学习，值得阅读的五本书籍，不看可能错失机会

今天为了总结一些可以帮助各位在学习过程中提供帮助的一些书籍。 一.鸟叔的私房菜&#xff1a; 本书是知名度颇高的Linux入门书《鸟哥的Linux私房菜基础学习篇》的新版,而详细地介绍了Linux操作系统。全书分为五部分;第一部分部分着重说明计算机的基础知识、Linux的学习方法&a…
阅读更多...
从零开始学习Linux（一）关闭虚拟机系统

从零开始学习Linux（一）关闭虚拟机系统

关闭系统&#xff0c;需要输入如下命令 poweroff然而&#xff0c;你只能得到如下反馈 -bash: poweroff:command not found此项错误是因为poweroff命令是一个系统管理命令。执行此项命令需要高级使用者特权。 因此&#xff0c;为了关闭系统&#xff0c;我们首先需要切换到root…
阅读更多...
个人随笔/小白应该如何学习Linux，我的一些心得分享.

个人随笔/小白应该如何学习Linux，我的一些心得分享.

大家好&#xff0c;今天给大家分享一下0基础的人如何入门Linux&#xff0c;此文来源&#xff1a;我在上班的路上看到一篇文章&#xff0c;也是写的0基础的人如何学习Linux的文章。当时我在想&#xff0c;我写博文一年多&#xff0c;都是相关Linux及Python等技术的文章&#xff…
阅读更多...
Linux学习路线

Linux学习路线

&#xfeff;&#xfeff; 关于 Linux Linux 因其开源&#xff0c;免费&#xff0c;可裁剪&#xff0c;被应用到很多领域&#xff0c;尤其是嵌入式设备上。 Android 系统内核也是基于 Linux 的。 另外还有各种服务器和工作站也是用的 Linux。 什么是嵌入式设备&#xff1f;…
阅读更多...
为什么要学习 Linux ？？？？

为什么要学习 Linux ？？？？

目前企业中大量的使用Linux作为服务器&#xff0c;在以后你们就业后&#xff0c;会发现web服务器Tomcat ,jobss这一类都是搭建在linux上面的&#xff0c;后面我们需要学习的数据库mysql &#xff0c; oracle &#xff0c;db2&#xff0c; 或者greenplum这一类的&#xff0c;在企…
阅读更多...
Linux 学习路线图

Linux 学习路线图

1.应用场景 更加高效地学习并达到运用Linux. 2.学习/操作 linux运维学习需要分为四个阶段&#xff1a;初级入门、中级进阶、高级提升、资深方向细化。 第一阶段&#xff1a;初级入门 初级阶段需要把linux学习路线搞清楚&#xff0c;任何学习都是循序渐进的&#xff0c;所以学…
阅读更多...
从零入门机器学习之Linux系统详解

从零入门机器学习之Linux系统详解

大家好，我是herosunly。985院校硕士毕业，现担任算法研究员一职，热衷于机器学习算法研究与应用。曾获得阿里云天池比赛第一名，科大讯飞比赛第三名，CCF比赛第四名。拥有多项发明专利。对机器学习和深度学习拥有自己独到的见解。曾经辅导过若干个非计算机专业的学生进入到算法…
阅读更多...
为什么要学习Linux？

为什么要学习Linux？

对于一些偶然接触到Linux的人来说&#xff0c;好奇是对于这个陌生名词的的第一印象。也许这个名字经常出现在你所使用的教科书上&#xff0c;或者是一些技术性的文章上&#xff0c;你却不知其意&#xff0c;此时这个名字再次出现&#xff0c;你就更是好奇了&#xff0c;Linux到…
阅读更多...
Linux学习总结

Linux学习总结

课程&#xff1a;Linux操作系统与应用 参考书&#xff1a;Linux从入门到精通、unix环境高级编程 学习linux之前必须要做好心理准备&#xff1a; 第一&#xff0c;要明白学好linux不是一件一蹴而就的事&#xff0c;一定要能坚持使用它&#xff0c;特别是在使用初期&#xff0c…
阅读更多...
你知道如何学习Linux吗？

你知道如何学习Linux吗？

说起Linux&#xff0c;业内人士或者经常玩电脑&#xff0c;对计算机比较精通的应该是比较熟悉的&#xff0c;Linux是一个开源的操作系统&#xff0c;由于其安全性高&#xff0c;完全免费&#xff0c;高效性&#xff0c;稳定等优点&#xff0c;越来越受大众的欢迎&#xff0c;就…
阅读更多...
学习linux的感受

学习linux的感受

学习前要 1.安装虚拟机或者自己买个云服务器 下载centOs然后将镜像装入系统 2.装入之后在自己的电脑下载Xshell和Xbox 3在自己windows系统下运行cmd拼一下自己的虚拟机或服务器测试两个机子网络是否相通&#xff0c;如果相通即可用Xshell进行远程登陆 成果: 今天学了vim与vi&…
阅读更多...
初学者如何系统性地学习Linux？

初学者如何系统性地学习Linux？

作为一个大一的同学&#xff0c;可以采取下面的步骤进行系统的学习Linux。 1、选择一个发行版&#xff1a;对于初学者&#xff0c;推荐使用Ubuntu或者Linux Mint。Ubuntu适合新手&#xff0c;使用广泛&#xff0c;社区活跃&#xff0c;遇到问题容易找到解决方案。虽然你觉得Ub…
阅读更多...
如何学习Linux

如何学习Linux

热热热 一、Linux大致要学习那些内容 1、Linux下的基本操作命令 2、Linux的各种配置 环境变量、网络的配置、服务的配置----常规而重要 3、Linux下搭建各种开发环境 例如&#xff1a; Javaee、大数据、Python等 4、能够写一些基本的shell脚本&#xff0c;对Linux系统进…
阅读更多...
QTP基本使用1

QTP基本使用1

目录 一、功能自动化 1、测试过程 2、录制类型 二、QTP基本使用1 1、【录制】 2、【运行】 3、【例 -- 录制编写记事本】 4、【设置】 三、上午程序脚本 四、test -- project 的比较 五、QTP基本使用2 1、导出test文件 2、导入test文件 3、查看帮助文档 4、修改…
阅读更多...
QTP 脚本语言编写入门到精通（一）

QTP 脚本语言编写入门到精通（一）

飞机订票登陆系统flight 一、编写用户登录测试用例。 二、直接编写脚本 ****************** SystemUtil.Run PathFinder.Locate("..\samples\flight\app\flight4a.exe"),"",PathFinder.Locate("..\samples\flight\app"),"open" Syst…
阅读更多...
QTP工具简单操作使用说明

QTP工具简单操作使用说明

简介 QTP是QuickTest Professional 的简称&#xff0c;是一种自动化测试工具。使用QTP的目的是用它来执行重复的手动测试&#xff0c;主要用于回归测试和测试同一软件的新版本&#xff08;版本迭代&#xff09;。 启动QuickTest 第一次启动QuickTest时&#xff0c;打开“加载…
阅读更多...
qt完整教程

qt完整教程

各个组件的意思（功能介绍） Python Qt GUI设计：UI界面可视化组件、属性概述（基础篇—3）-腾讯云开发者社区-腾讯云 qt 如何设计好布局和漂亮的界面。_qt界面_花狗Fdog的博客-CSDN博客 样式表（美化关键）/*灰色*/ Q/*灰色*/ QWidget {background-color: rgb(255, 182, …
阅读更多...
QT5教程推荐

QT5教程推荐

学完《C Primer》该学什么&#xff1f;《Qt 5.9 C开发指南》是一个不错的选择。两本书结合是C岗位就业的保障。Qt的书籍很多&#xff0c;推荐这一本是因为更接近实战&#xff08;工作内容&#xff09;。理论和实际结合的很好。虽然Qt6.x已经问世&#xff0c;但学习Qt5.9并不过时…
阅读更多...
推荐文章

Copyright @ 2022~2023