二叉树的四种遍历方式

article/2025/10/8 18:16:08

概要

树本身是一种简单化的图 ；
DFS对应前中后序遍历，BFS对应层序遍历

二叉树结构

  struct treenode {int val;treenode *left;treenode *right;treenode() : val(0), left(nullptr), right(nullptr) {}treenode(int x) : val(x), left(nullptr), right(nullptr) {}treenode(int x, treenode *left, treenode *right) : val(x), left(left), right(right) {}};

1-中序遍历

二叉树的中序遍历就是首先遍历左子树，然后访问当前节点，最后遍历右子树。对于下面的二叉树，中序遍历结果如下：
在这里插入图片描述
直观来看，二叉树的中序遍历就是将节点投影到一条水平的坐标上。如图：
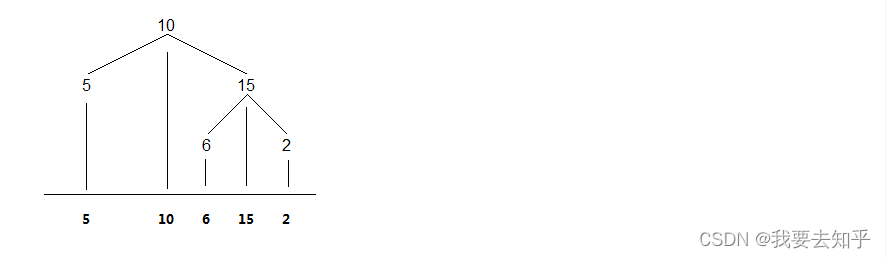
在这里插入图片描述

方法一：递归

这是思路最简单的方法，容易想到并且容易实现。递归的终止条件是当前节点是否为空。首先递归调用遍历左子树，然后访问当前节点，最后递归调用右子树。代码如下：

//recursive
class Solution1 {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> ret;if(root==NULL)return ret;inorderHelper(ret,root);return ret;}
private:void inorderHelper(vector<int>& ret,TreeNode* root){if(root==NULL)return;inorderHelper(ret,root->left);ret.push_back(root->val);inorderHelper(ret,root->right);}
};
  1. 时间复杂度：O(n)，其中 n 为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。
  2. 空间复杂度：O(n)。空间复杂度取决于递归的栈深度，而栈深度在二叉树为一条链的情况下会达到 O(n) 的级别。

方法二：迭代

在迭代方法中，从根节点开始找二叉树的最左节点，将走过的节点保存在一个栈中，找到最左节点后访问，对于每个节点来说，它都是以自己为根的子树的根节点，访问完之后就可以转到右儿子上了。代码如下：

class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> res;stack<TreeNode*> stk;while (root != nullptr || !stk.empty()) {while (root != nullptr) {stk.push(root);  //要在循环之后执行push(root)root = root->left;}root = stk.top();stk.pop();res.push_back(root->val);root = root->right;}return res;}
};

时间复杂度和空间复杂度同递归。
非递归的空间复杂度和二叉树的深度和高度有关

方法三：Morris 中序遍历

Morris 遍历算法是另一种遍历二叉树的方法，它能将非递归的中序遍历空间复杂度降为 O(1)。

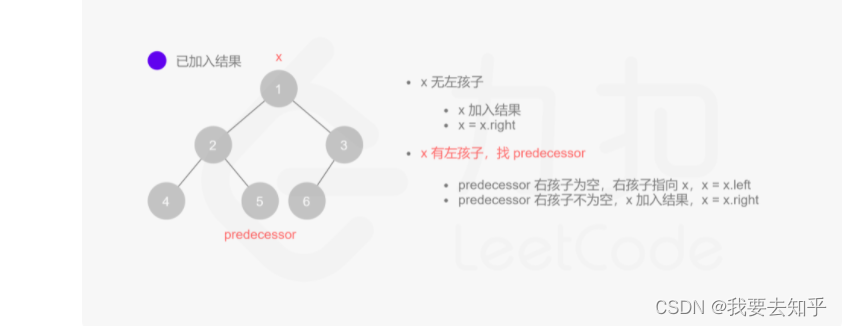
Morris 遍历算法整体步骤如下（假设当前遍历到的节点为 x）：

如果 x 无左孩子，先将 x 的值加入答案数组，再访问 x 的右孩子，即 x=x.right。
如果 x 有左孩子，则找到 x 左子树上最右的节点（即左子树中序遍历的最后一个节点，x 在中序遍历中的前驱节点），我们记为 predecessor。根据 predecessor 的右孩子是否为空，进行如下操作。
如果predecessor 的右孩子为空，则将其右孩子指向 x，然后访问 x 的左孩子，即 x=x.left。
如果predecessor 的右孩子不为空，则此时其右孩子指向 x，说明我们已经遍历完 x 的左子树，我们将predecessor 的右孩子置空，将 x 的值加入答案数组，然后访问 x 的右孩子，即 x=x.right。
重复上述操作，直至访问完整棵树。

在这里插入图片描述

class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> res;TreeNode *predecessor = nullptr;while (root != nullptr) {if (root->left != nullptr) {// predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止predecessor = root->left;while (predecessor->right != nullptr && predecessor->right != root) {predecessor = predecessor->right;}// 让 predecessor 的右指针指向 root，继续遍历左子树if (predecessor->right == nullptr) {predecessor->right = root;root = root->left;}// 说明左子树已经访问完了，我们需要断开链接else {res.push_back(root->val);predecessor->right = nullptr;root = root->right;}}// 如果没有左孩子，则直接访问右孩子else {res.push_back(root->val);root = root->right;}}return res;}
};
  1. 时间复杂度：O(n)，其中 nn 为二叉搜索树的节点个数。Morris 遍历中每个节点会被访问两次，因此总时间复杂度为 O(2n)=O(n)。
  2. 空间复杂度：O(1)。

2-先序遍历

方法一：递归

调整下访问顺序即可。代码如下：

//recursion
class Solution1 {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> ret;preHelper(ret,root);return ret;}
private:void preHelper(vector<int>& ret,TreeNode* root){if(root==NULL)return;ret.push_back(root->val);preHelper(ret,root->left);preHelper(ret,root->right);}
};

class Solution:def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:l=[]def dfs(root:Optional[TreeNode])->List[int]:if not root:return Nonel.append(root.val)dfs(root.left)dfs(root.right)return ldfs(root)return l

方法二：迭代

迭代法使用一个栈来保存当前不需要访问的节点。从根节点开始，访问当前节点，按照先右儿子后左儿子的顺序将当前节点的两个儿子压栈。当栈为空时说明遍历完毕。代码如下：

//iterative
class Solution2 {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> ret;stack<TreeNode*> st;if(root==NULL)return ret;st.push(root);while(!st.empty()){TreeNode *curr=st.top();st.pop();if(curr->right)st.push(curr->right);if(curr->left)st.push(curr->left);ret.push_back(curr->val);}return ret;}
};

class Solution:def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:res=list()stk=[]if not root:return resstk.append(root)while stk:node=stk.pop()if node.right:stk.append(node.right)if node.left:stk.append(node.left)res.append(node.val)return res
  1. 时间复杂度 O(N) ： 其中 N 为二叉树的节点数量，建立二叉树镜像需要遍历树的所有节点，占用 O(N) 时间。
  2. 空间复杂度 O(N) ：最差情况下，栈 stack 最多同时存储 (N+1)/2个节点(N最差的情况下只能为奇数)，占用 O(N) 额外空间。

方法三：Morris 先序遍历

前序遍历和中序遍历的Morris方法基本一样，不同之处在访问的顺序。代码如下：

//Morris
class Solution3 {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> ret;if(root==NULL)return ret;TreeNode *curr=root;TreeNode *pre;while(curr){if(curr->left==NULL){ret.push_back(curr->val);curr=curr->right;}else{pre=curr->left;while(pre->right&&pre->right!=curr)pre=pre->right;if(pre->right==NULL){ret.push_back(curr->val);pre->right=curr;curr=curr->left;}else{pre->right=NULL;curr=curr->right;}}}return ret;}
};

class Solution:def preorderTraversal(self, root: TreeNode) -> List[int]:res = list()if not root:return resp1 = rootwhile p1:p2 = p1.leftif p2:while p2.right and p2.right != p1:p2 = p2.rightif not p2.right:res.append(p1.val)p2.right = p1p1 = p1.leftcontinueelse:p2.right = Noneelse:res.append(p1.val)p1 = p1.rightreturn res

3-层序遍历

二叉树的层序遍历：一般基于队列的实现

首先将二叉树的根节点push到队列中。
判断队列不为空就输出队头元素。
判断当前对头节点是否有孩子节点，有则push到队列中。
循环操作，直到队列为空。

方法一：迭代

vector<int> levelOrder(TreeNode* Tree) //层序遍历_队列实现
{vector<int>res;queue < TreeNode* > q;if (Tree != NULL)q.push(Tree);   //根节点进队列while (q.empty() == false)  //队列不为空{TreeNode* node=q.front();res.push_back(node->val); if (node->left != NULL)   //如果有左孩子，入队q.push(node->left);   if (node->right != NULL)   //如果有右孩子，入队q.push(node->right);q.pop();  //已经遍历过的节点出队列}return res;
}
  1. 时间复杂度：O（N）,N 为二叉树的节点数量，即 BFS 需循环 N 次。
  2. 空间复杂度：O（N）,最差情况下，即当树为平衡二叉树时，最多有 N/2 个树节点同时在 queue 中，使用O(N) 大小的额外空间。

方法二a：分行进行层序遍历

class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> res;vector<int> level_data;if(root==NULL)return res;queue<TreeNode*> q;q.push(root);q.push(NULL);while(!q.empty()){TreeNode* temp=q.front();q.pop();if(temp){level_data.push_back(temp->val);if(temp->left)q.push(temp->left);if(temp->right)q.push(temp->right);}else{if(!level_data.empty()){q.push(NULL);res.push_back(level_data);level_data.clear();}}}return res;}
};

方法三： leetcode形式

可以归纳出这样的循环不变式：第 i 次迭代前，队列中的所有元素就是第 i 层的所有元素，并且按照从左向右的顺序排列。证明它的三条性质（你也可以把它理解成数学归纳法）：

初始化：i=1 的时候，队列里面只有 root，是唯一的层数为 1 的元素，因为只有一个元素，所以也显然满足「从左向右排列」；
保持：如果 i=k 时性质成立，即第 k 轮中出队sk ​ 的元素是第 k层的所有元素，并且顺序从左到右。因为对树进行广度优先搜索的时候由低 k 层的点拓展出的点一定也只能是 k+1 层的点，并且 k+1 层的点只能由第 k 层的点拓展到，所以由这 sk ​个点能拓展到下一层所有的 sk+1 ​个点。又因为队列的先进先出（FIFO）特性，既然第 k 层的点的出队顺序是从左向右，那么第 k+1层也一定是从左向右。至此，我们已经可以通过数学归纳法证明循环不变式的正确性。
终止：因为该循环不变式是正确的，所以按照这个方法迭代之后每次迭代得到的也就是当前层的层次遍历结果。至此，我们证明了算法是正确的。

class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector <vector <int>> ret;if (!root) {return ret;}queue <TreeNode*> q;q.push(root);while (!q.empty()) {int currentLevelSize = q.size();ret.push_back(vector <int> ());for (int i = 1; i <= currentLevelSize; ++i) {auto node = q.front(); q.pop();ret.back().push_back(node->val);if (node->left) q.push(node->left);if (node->right) q.push(node->right);}}  return ret;}
};
  1. 时间复杂度：每个点进队出队各一次，故渐进时间复杂度为 O(n)，树上所有节点的个数为n。
  2. 空间复杂度：队列中元素的个数不超过 n 个，故渐进空间复杂度为O(n)，满二叉树的时候队列元素是最多的。

二叉树的层序遍历II

给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {vector<vector<int>>ret;if(!root)return ret;queue<TreeNode*>q;q.push(root);while(!q.empty()){int currentLevelSize=q.size();ret.push_back(vector<int>());for(int i=1;i<=currentLevelSize;++i){auto node=q.front();q.pop();ret.back().push_back(node->val);if(node->left)q.push(node->left);if(node->right)q.push(node->right);}}reverse(ret.begin(),ret.end());return ret;}
};
  1. 时间复杂度：O（n）
  2. 空间复杂度：O（n）

扩展：之字形打印二叉树

利用两个栈

//按之字形打印void Print(TreeNode *root){if (root == NULL)return;stack<TreeNode*>levels[2];int current = 0, next = 1;levels[current].push(root);while (!levels[0].empty() || !levels[1].empty()){TreeNode*node = levels[current].top();levels[current].pop();printf("%d", node->val);if (current == 0){if (node->left != nullptr)levels[next].push(node->left);if (node->right != nullptr)levels[next].push(node->right);}else{if (node->right != nullptr)levels[next].push(node->right);if (node->left != nullptr)levels[next].push(node->left);}if (levels[current].empty()){cout << endl;current = 1 - current;next = 1 - next;}}}
  1. 时间复杂度：每个点进栈出栈各一次，故渐进时间复杂度为 O(n)，树上所有节点的个数为n。
  2. 空间复杂度：栈中元素的个数不超过 n 个，故渐进空间复杂度为O(n)，满二叉树的时候栈的元素是最多的。

二叉树的锯齿形层序遍历

class Solution {
public:vector<vector<int>> zigzagLevelOrder(TreeNode* root) {vector<vector<int>>vec;if(root==NULL)return vec;stack<TreeNode*>levels[2];int current=0,next=1;levels[current].push(root);vec.push_back(vector<int>());while(!levels[current].empty()||!levels[next].empty()){TreeNode *pNode=levels[current].top();levels[current].pop();if(pNode==NULL)continue;vec.back().push_back(pNode->val);if(current==0){if(pNode->left)levels[next].push(pNode->left);if(pNode->right)levels[next].push(pNode->right);               }else{if(pNode->right)levels[next].push(pNode->right);if(pNode->left)levels[next].push(pNode->left);     }if(levels[current].empty()){vec.push_back(vector<int>());current=1-current;next=1-next;}}vec.pop_back();return vec;}
};

4-后序遍历

方法一：递归

//recursion
class Solution1 {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> ret;postHelper(ret,root);return ret;}
private:void postHelper(vector<int>& ret,TreeNode* root){if(root==NULL)return;postHelper(ret,root->left);postHelper(ret,root->right);ret.push_back(root->val);}
};
  1. 时间复杂度：O（N）
  2. 空间复杂度：O（N）

方法二：迭代

迭代法使用一个栈来保存当前不需要访问的节点。不过，不同于中序遍历与前序遍历，在后序遍历中每一个节点需要一个标志位，来标识当前节点的左右子树是否被访问。因为在后序遍历中，只有一个节点的左右子树被访问后它才能被访问。因此，压入栈中的数据类型需要是一个pair<TreeNode*,int>，其中用1来表示当前节点的左右子树正被访问，当再次访问到此节点时可以访问此节点；用0表示当前节点的左右子树未被访问，再次访问到此节点时需要首先访问此节点的左右子树。

//iteration
class Solution1 {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> ret;if(root==NULL)return ret;stack<pair<TreeNode*,int>> st;st.push(make_pair(root,0));while(!st.empty()){TreeNode *curr=st.top().first;if(st.top().second==1){ret.push_back(curr->val);st.pop();}else{st.top().second=1;if(curr->right)st.push(make_pair(curr->right,0));if(curr->left)st.push(make_pair(curr->left,0));}}return ret;}
};
  1. 时间复杂度：O（N），每个节点需访问两次
  2. 空间复杂度：O（N）

方法三：迭代法

这种方法就是按照根、右、左的顺序访问，然后将结果取反即可。后序遍历的顺序是左、右、根。这种方法就可以在前序遍历的基础上修改即可。代码如下：

class Solution3 {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> ret;if(root==NULL)return ret;stack<TreeNode*> st;st.push(root);while(!st.empty()){TreeNode *curr=st.top();st.pop();if(curr->left)st.push(curr->left);if(curr->right)st.push(curr->right);ret.push_back(curr->val);}reverse(ret.begin(),ret.end());return ret;}
};
  1. 时间复杂度：O（N），按照根、右、左的顺序遍历时，每个节点被访问一次，将结果取反时，每个节点也被访问一次，所以每个节点需访问两次
  2. 空间复杂度：O（N）

Morris方法

后序遍历的Morris方法思路比较难。但整体上还是一样的，对原来的二叉树的修改也是一样的，不同的是访问的顺序。而在后序遍历中，访问时比较麻烦。下面是整个算法的工作过程;

首先建立一个临时节点dump，令其左儿子是root。并且还需要一个子过程，就是倒序输出某两个节点之间路径上的各个节点。
步骤：
当前节点设置为临时节点dump。
（1）如果当前节点的左儿子为空，则将其右儿子作为当前节点；
（2）如果当前节点的左儿子非空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点；
a) 如果前驱节点的右孩子为空，将它的右儿子设置为当前节点。当前节点更新为当前节点的左儿子；
b) 如果前驱节点的右儿子为当前节点，将它的右孩子重新设为空。倒序输出从当前节点的左儿子到该前驱节点这条路径上的所有节点。当前节点更新为当前节点的右儿子；
（3）重复以上（1）（2）直到当前节点为空。

代码如下：

//morris
class Solution4 {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> ret;TreeNode *dump=new TreeNode(0);dump->left=root;TreeNode *curr=dump;TreeNode *pre;while(curr){if(curr->left==NULL){curr=curr->right;}else{pre=curr->left;while(pre->right&&pre->right!=curr)pre=pre->right;if(pre->right==NULL){pre->right=curr;curr=curr->left;}else{reverseAddNodes(curr->left,pre,ret);pre->right=NULL;curr=curr->right;}}}return ret;}
private:void reverseAddNodes(TreeNode *begin,TreeNode *end,vector<int>& ret){reverseNodes(begin,end);TreeNode *curr=end;while(true){ret.push_back(curr->val);if(curr==begin)break;curr=curr->right;}reverseNodes(end,begin);}void reverseNodes(TreeNode *begin,TreeNode *end){TreeNode *pre=begin;TreeNode *curr=pre->right;TreeNode *post;while(pre!=end){post=curr->right;curr->right=pre;pre=curr;curr=post;}}
};
  1. 时间复杂度：O（N）
  2. 空间复杂度：O（1）

http://chatgpt.dhexx.cn/article/kEw5Xplc.shtml

相关文章

针对Linux学习，值得阅读的五本书籍，不看可能错失机会

针对Linux学习，值得阅读的五本书籍，不看可能错失机会

今天为了总结一些可以帮助各位在学习过程中提供帮助的一些书籍。 一.鸟叔的私房菜&#xff1a; 本书是知名度颇高的Linux入门书《鸟哥的Linux私房菜基础学习篇》的新版,而详细地介绍了Linux操作系统。全书分为五部分;第一部分部分着重说明计算机的基础知识、Linux的学习方法&a…
阅读更多...
从零开始学习Linux（一）关闭虚拟机系统

从零开始学习Linux（一）关闭虚拟机系统

关闭系统&#xff0c;需要输入如下命令 poweroff然而&#xff0c;你只能得到如下反馈 -bash: poweroff:command not found此项错误是因为poweroff命令是一个系统管理命令。执行此项命令需要高级使用者特权。 因此&#xff0c;为了关闭系统&#xff0c;我们首先需要切换到root…
阅读更多...
个人随笔/小白应该如何学习Linux，我的一些心得分享.

个人随笔/小白应该如何学习Linux，我的一些心得分享.

大家好&#xff0c;今天给大家分享一下0基础的人如何入门Linux&#xff0c;此文来源&#xff1a;我在上班的路上看到一篇文章&#xff0c;也是写的0基础的人如何学习Linux的文章。当时我在想&#xff0c;我写博文一年多&#xff0c;都是相关Linux及Python等技术的文章&#xff…
阅读更多...
Linux学习路线

Linux学习路线

&#xfeff;&#xfeff; 关于 Linux Linux 因其开源&#xff0c;免费&#xff0c;可裁剪&#xff0c;被应用到很多领域&#xff0c;尤其是嵌入式设备上。 Android 系统内核也是基于 Linux 的。 另外还有各种服务器和工作站也是用的 Linux。 什么是嵌入式设备&#xff1f;…
阅读更多...
为什么要学习 Linux ？？？？

为什么要学习 Linux ？？？？

目前企业中大量的使用Linux作为服务器&#xff0c;在以后你们就业后&#xff0c;会发现web服务器Tomcat ,jobss这一类都是搭建在linux上面的&#xff0c;后面我们需要学习的数据库mysql &#xff0c; oracle &#xff0c;db2&#xff0c; 或者greenplum这一类的&#xff0c;在企…
阅读更多...
Linux 学习路线图

Linux 学习路线图

1.应用场景 更加高效地学习并达到运用Linux. 2.学习/操作 linux运维学习需要分为四个阶段&#xff1a;初级入门、中级进阶、高级提升、资深方向细化。 第一阶段&#xff1a;初级入门 初级阶段需要把linux学习路线搞清楚&#xff0c;任何学习都是循序渐进的&#xff0c;所以学…
阅读更多...
从零入门机器学习之Linux系统详解

从零入门机器学习之Linux系统详解

大家好，我是herosunly。985院校硕士毕业，现担任算法研究员一职，热衷于机器学习算法研究与应用。曾获得阿里云天池比赛第一名，科大讯飞比赛第三名，CCF比赛第四名。拥有多项发明专利。对机器学习和深度学习拥有自己独到的见解。曾经辅导过若干个非计算机专业的学生进入到算法…
阅读更多...
为什么要学习Linux？

为什么要学习Linux？

对于一些偶然接触到Linux的人来说&#xff0c;好奇是对于这个陌生名词的的第一印象。也许这个名字经常出现在你所使用的教科书上&#xff0c;或者是一些技术性的文章上&#xff0c;你却不知其意&#xff0c;此时这个名字再次出现&#xff0c;你就更是好奇了&#xff0c;Linux到…
阅读更多...
Linux学习总结

Linux学习总结

课程&#xff1a;Linux操作系统与应用 参考书&#xff1a;Linux从入门到精通、unix环境高级编程 学习linux之前必须要做好心理准备&#xff1a; 第一&#xff0c;要明白学好linux不是一件一蹴而就的事&#xff0c;一定要能坚持使用它&#xff0c;特别是在使用初期&#xff0c…
阅读更多...
你知道如何学习Linux吗？

你知道如何学习Linux吗？

说起Linux&#xff0c;业内人士或者经常玩电脑&#xff0c;对计算机比较精通的应该是比较熟悉的&#xff0c;Linux是一个开源的操作系统&#xff0c;由于其安全性高&#xff0c;完全免费&#xff0c;高效性&#xff0c;稳定等优点&#xff0c;越来越受大众的欢迎&#xff0c;就…
阅读更多...
学习linux的感受

学习linux的感受

学习前要 1.安装虚拟机或者自己买个云服务器 下载centOs然后将镜像装入系统 2.装入之后在自己的电脑下载Xshell和Xbox 3在自己windows系统下运行cmd拼一下自己的虚拟机或服务器测试两个机子网络是否相通&#xff0c;如果相通即可用Xshell进行远程登陆 成果: 今天学了vim与vi&…
阅读更多...
初学者如何系统性地学习Linux？

初学者如何系统性地学习Linux？

作为一个大一的同学&#xff0c;可以采取下面的步骤进行系统的学习Linux。 1、选择一个发行版&#xff1a;对于初学者&#xff0c;推荐使用Ubuntu或者Linux Mint。Ubuntu适合新手&#xff0c;使用广泛&#xff0c;社区活跃&#xff0c;遇到问题容易找到解决方案。虽然你觉得Ub…
阅读更多...
如何学习Linux

如何学习Linux

热热热 一、Linux大致要学习那些内容 1、Linux下的基本操作命令 2、Linux的各种配置 环境变量、网络的配置、服务的配置----常规而重要 3、Linux下搭建各种开发环境 例如&#xff1a; Javaee、大数据、Python等 4、能够写一些基本的shell脚本&#xff0c;对Linux系统进…
阅读更多...
QTP基本使用1

QTP基本使用1

目录 一、功能自动化 1、测试过程 2、录制类型 二、QTP基本使用1 1、【录制】 2、【运行】 3、【例 -- 录制编写记事本】 4、【设置】 三、上午程序脚本 四、test -- project 的比较 五、QTP基本使用2 1、导出test文件 2、导入test文件 3、查看帮助文档 4、修改…
阅读更多...
QTP 脚本语言编写入门到精通（一）

QTP 脚本语言编写入门到精通（一）

飞机订票登陆系统flight 一、编写用户登录测试用例。 二、直接编写脚本 ****************** SystemUtil.Run PathFinder.Locate("..\samples\flight\app\flight4a.exe"),"",PathFinder.Locate("..\samples\flight\app"),"open" Syst…
阅读更多...
QTP工具简单操作使用说明

QTP工具简单操作使用说明

简介 QTP是QuickTest Professional 的简称&#xff0c;是一种自动化测试工具。使用QTP的目的是用它来执行重复的手动测试&#xff0c;主要用于回归测试和测试同一软件的新版本&#xff08;版本迭代&#xff09;。 启动QuickTest 第一次启动QuickTest时&#xff0c;打开“加载…
阅读更多...
qt完整教程

qt完整教程

各个组件的意思（功能介绍） Python Qt GUI设计：UI界面可视化组件、属性概述（基础篇—3）-腾讯云开发者社区-腾讯云 qt 如何设计好布局和漂亮的界面。_qt界面_花狗Fdog的博客-CSDN博客 样式表（美化关键）/*灰色*/ Q/*灰色*/ QWidget {background-color: rgb(255, 182, …
阅读更多...
QT5教程推荐

QT5教程推荐

学完《C Primer》该学什么&#xff1f;《Qt 5.9 C开发指南》是一个不错的选择。两本书结合是C岗位就业的保障。Qt的书籍很多&#xff0c;推荐这一本是因为更接近实战&#xff08;工作内容&#xff09;。理论和实际结合的很好。虽然Qt6.x已经问世&#xff0c;但学习Qt5.9并不过时…
阅读更多...
qtp11安装及入门

qtp11安装及入门

一、简介 QTP是Quick Test Professional的简称&#xff0c;是一种自动测试工具。使用QTP的目的是想用它来执行重复的自动化测试&#xff0c;主要是用于回归测试和测试同一软件的新版本。因此你在测试前要考虑好如何对应用程序进行测试&#xff0c;例如要测试哪些功能、操作步骤…
阅读更多...
QTP软件测试工具学习

QTP软件测试工具学习

一、定义 QTP&#xff1a;&#xff08;QuickTest Professional&#xff09;&#xff0c;是一款用于功能测试的自动化测试工具&#xff0c;常用于Web网页测试和Windows窗体程序的测试&#xff0c;使用的脚本语言是VBScript&#xff0c;也可以直接录制生成测试脚本。在QTP8.0之后…
阅读更多...
推荐文章

Copyright @ 2022~2023