from https://blog.zhjh.top/archives/XokySA7Rc1pkVvnxAEP5E
前提是系统为 Windows 10 22H2 10.0.19045.2311 或更高版本,尽量新。
步骤
使用 WSAPatch 和 MagiskOnWSALocal 安装 WSA
-
在 Microsoft Store 中安装 Ubuntu LTS(或你喜欢的发行版),此处为 Ubuntu 20.04.5 LTS。

-
开始菜单找到并打开安装的 Ubuntu,执行以下命令。Linux 子系统的 /mnt 目录,可以访问到 Windows 的文件系统。
2.1 克隆 MagiskOnWSALocal 仓库,如果卡住不动请合理使用代理或搜索“github 镜像站”(要确保更新到了最新!)。
git clone https://github.com/LSPosed/MagiskOnWSALocal.git --depth 12.2 运行脚本。等待一段时间后,使用 Tab 键和方向键切换选项,使用空格选中选项。
cd MagiskOnWSALocal ./scripts/run.sh2.3 选择符合你系统的类型(x64/arm64)。

2.4 WSA 版本推荐选择 insider fast (Dev Channel)。
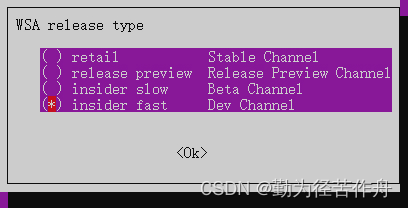
2.5 选择是否 Root。

2.6 选择 Root 类型,如果对隐藏 Root 没有非常强烈的要求就选择 Magisk。自行搜索 Magisk 和 KernelSU 的区别。
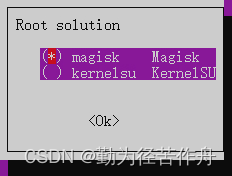
2.7 Magisk 版本推荐选择 stable (Stable Channel)。
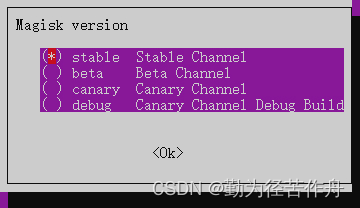
2.8 自行选择是否安装 GApps(Google 套件)。
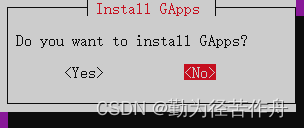
2.9 自行选择是否保留 Amazon Appstore。
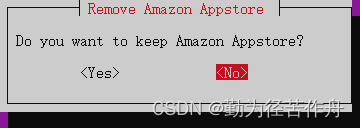
2.10 选择 Root 解决方案。
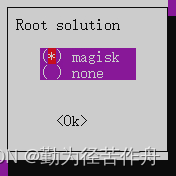
2.11 选择压缩输出,压缩格式自由选择。
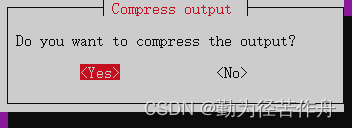
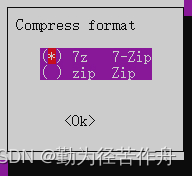
-
将 MagiskOnWSALocal 生成的压缩包复制出来并解压(下文称为“WSA 文件夹”)。以下命令为示例。
cp output/WSA_xxx.7z /mnt/e/xxx/
-
下载 WSAPatch 的最新 Release,将其中的 WsaPatch.dll 和 icu.dll 复制到 WSA 文件夹的 WsaClient 中。
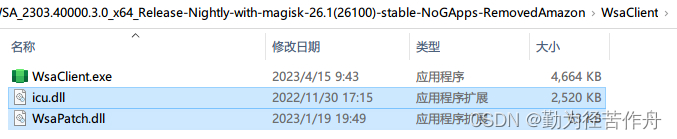
-
修改 WSA 文件夹中的
AppxManifest.xml并保存。5.1 将
TargetDeviceFamily节点的MinVersion属性的值由10.0.22000.120改为10.0.19045.2311。<TargetDeviceFamily Name="Windows.Desktop" MinVersion="10.0.19045.2311" MaxVersionTested="10.0.22000.120" />5.2 搜索
customInstall,将相关节点删除。<rescap:Capability Name="customInstallActions" /><desktop6:Extension Category="windows.customInstall"><desktop6:CustomInstall Folder="CustomInstall" desktop8:RunAsUser="true"><desktop6:RepairActions><desktop6:RepairAction File="WsaSetup.exe" Name="Repair" Arguments="repair" /></desktop6:RepairActions><desktop6:UninstallActions><desktop6:UninstallAction File="WsaSetup.exe" Name="Uninstall" Arguments="uninstall" /></desktop6:UninstallActions></desktop6:CustomInstall> </desktop6:Extension> -
以管理员身份运行 WSA 文件夹的
Run.bat,如果闪退就双击运行。
注意事项:WSAPatch/README_zhs.md#注意事项 at main · cinit/WSAPatch
如果想卸载 WSA,可以在系统设置 - 应用 - 应用和功能中找到。

使用 WSA 工具箱安装 APK
- 在 Microsoft Store 中安装 WSA 工具箱。
- 打开 WSA 工具箱,在“故障诊断”中点击第二个“点击此处”以打开 WSA。
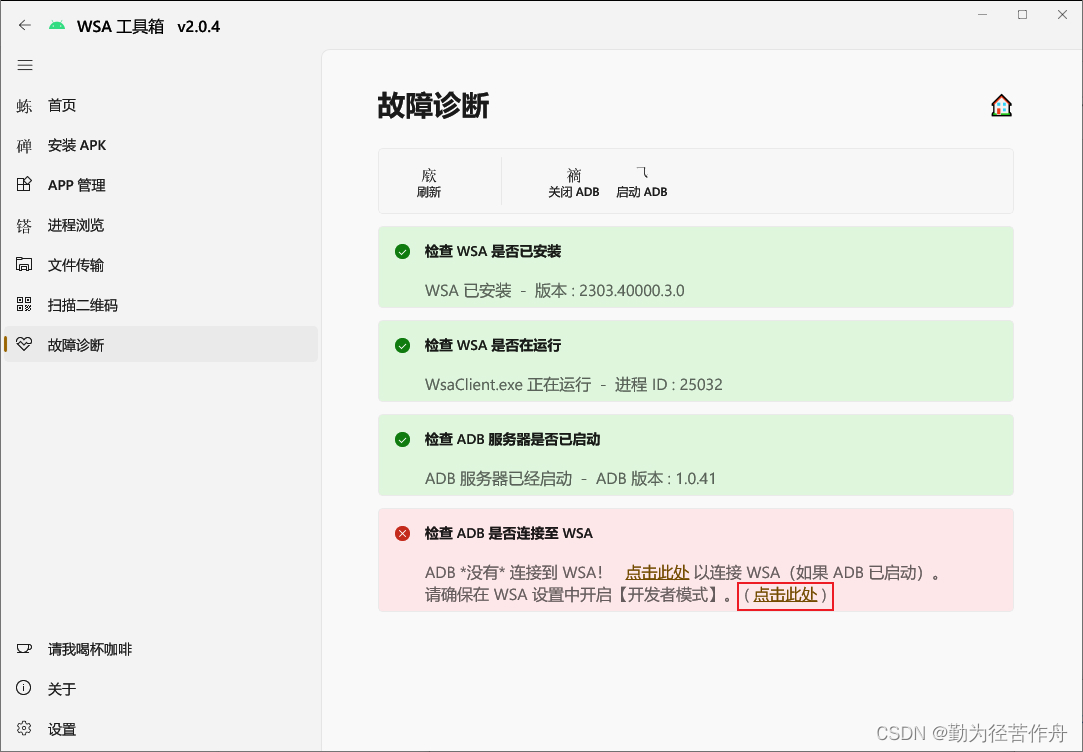
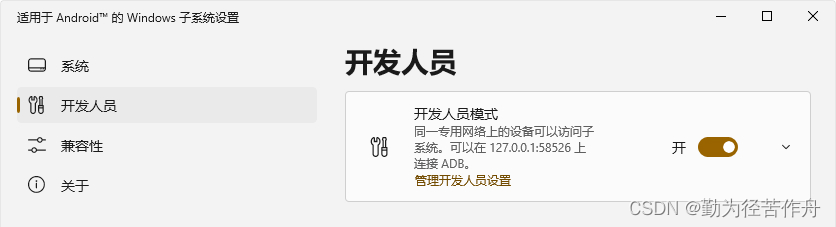
- 开启
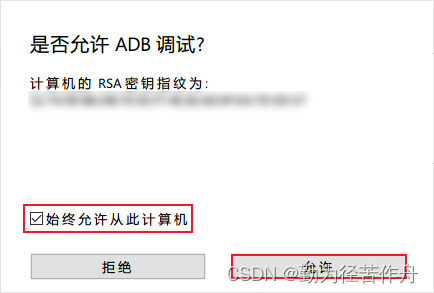
开发人员模式,在 WSA 工具箱的“故障诊断”中点击第一个“点击此处”以连接 WSA,并在“是否运行 ADB 调试”的弹框中勾选“始终允许从此计算机”后允许。

- 在 WSA 工具箱的“安装 APK”中“选择 APK”,然后勾选需要安装的 APK,点击“安装选中项”即可。

- 安装后可以在 WSA 工具箱的“APP 管理”中运行或者按 Win 键在开始菜单中搜索运行。
参考
- cinit/WSAPatch: Make WSA(Windows Subsystem for Android) run on Windows 10.
- LSPosed/MagiskOnWSALocal: Integrate Magisk root and Google Apps into WSA (Windows Subsystem for Android)