【LineageOS】编译安装及windows下推送更新记录
- 背景说明
- 编译
- 安装
- GApps 安装
- windows下推送更新
背景说明
AOSP装谷歌服务,遇到很多问题,于是选择其它的rom,之前装了piexlExperience没有成功,后来又换了LineageOS,终于成功了。官方的教程写的都很好,但是仍遇到了一些坑,所以做些记录。
这里只记录遇到的坑,具体流程,不同手机也有不同,所以跟随官方教程。
我的手机是:Google Piexl 3xl 安装Android 12 选则最新的 19.1分支
编译
https://wiki.lineageos.org/devices/crosshatch/build
前面没啥好说的,就是注意改路径的话,各个地方都得改,比如你的bin目录换地方了,后面把bin加到.profile文件的路径都记得改。
值得提的三点:
- 更改清华源的问题,我这里没有改,我按照清华镜像网站上的教程,改完了反而报错了,不知道什么情况,我自己有挂代理所以也不存在下载问题,所以就没有换源了。
- repo sync 问题,至少加个 -c命令,减少硬盘空间需求。顺便,我在源码修改后,仅运行 repo sync -c是没有把我的更改覆盖的,可能需要force 之类的命令才会覆,对repo没有特别了解。
- 提取专有 blob ,里面有说
将 blob 拉入~/android/lineage/vendor/google文件夹中但是我没明白怎么个拉入法,我比较了下我这个文件夹和我其它rom仓库下同样文件夹的区别,我发现已经没有区别了,所以就没管,也成了。 - 提取blob的时候 https://wiki.lineageos.org/extracting_blobs_from_zips
a. 我的手机是基于负载的 OTA:系统分区的内容存储.img为payload.bin我从官方zip中提取了payload.bin,
b. 安装sudo apt-get install python-protobuf,但是这样之后还是报错,根据报错网上查了一下,单独分别安装了pip install protobuf,就成了,应该还有个包,根据报错网上查一下应该就能找到
c. 好像还有个包需要降级,但是也都不是什么困难的问题,根据报错很容易就能解决
d. 挂载的时候,我的手机分区就没有odm,所以这一步sudo mount -o ro odm.img system/odm/包括后面有一不可能也会有报错,但是不影响。
e. 在~/android/lineage/device/google/crosshatch文件夹下运行脚本后就完成了。
安装
官方教程:https://wiki.lineageos.org/devices/bluejay/install
我这里流程简化为:
刷入:
- 官方recovery安装:
fastboot模式下输入命令:fastboot flash boot <recovery_filename>.img(fastboot flash 和 fastboot boot的合体命令)
这里刷入我们编译好后给的boot.img文件
Use the menu to navigate to and to select the Recovery option
- 使用recovery刷入:
选择,Factory Reset, then Format data / factory reset
需要清理数据,不然好像会有问题。
“Apply Update”, then “Apply from ADB” 电脑上输入命令adb sideload filename.zip
如果不装GApps可以重启开机了,但是装的话千万不能直接重启。
GApps 安装
首先提前下载和自己版本一致的 GApps的包。
https://wiki.lineageos.org/gapps
- 在第一次打开OS之前进行刷入(也就是说上面刷机完成不要打开系统!!先选择
Advanced,重新Reboot to Recovery) - 即使您已经在恢复中,请单击
Advanced,然后Reboot to Recovery - Apply Update - ADB sideload - MineGApps.zip文件
windows下推送更新
刷机的方式需要清除数据,所以很多时候不太方便,这时可以考虑如何系统更新,而不是直接刷机。(因为修改源码后重新编译打包,经常有系统更新的需求)
这里的更新指的是一个版本下的更新,另外还有不同版本的升级更新,官方另有教程。
官方提供的教程中,推送更新脚本只能在linux和macOS上运行。https://wiki.lineageos.org/devices/crosshatch/update
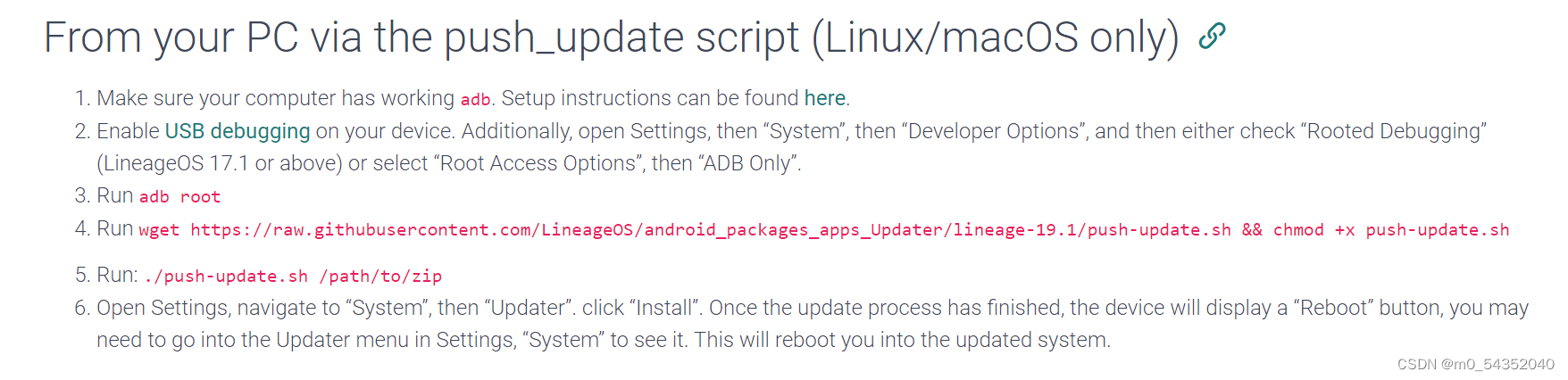
首先,需要解决在windows下执行shell脚本的问题。
这里通过搜索我选择的办法是安装 cygwin http://www.cygwin.com/
直接官网上下载,按照教程安装就行。安装完成后即得到可以运行的脚本的命令行。
事实上,安装好之后,问题就解决了。
按照教程:
- 打开开发者选项中的 adb root
- 下载脚本并设置权限
wget https://raw.githubusercontent.com/LineageOS/android_packages_apps_Updater/lineage-19.1/push-update.sh
chmod +x push-update.sh
wget并不内置在cgywin中,需要安装,如果直接打开浏览器下载复制保存脚本,可能有‘\r’这种空白符的问题,但是我并不确定,不想安装可以仓库的Linux系统下下载然后转移过来。
3.运行脚本,注意 /cygdrive/是cygwin对自己电脑和它路径的映射,具体可以使用mount命令看一下,在运行脚本的时候,push-update.sh 是要在cygwin中运行,所以是给cygwin看的路径,但是后面刷机包的路径,是给脚本内的adb命令看的路径,所以要使用实际真实的路径名。
/cygdrive/f/LinOS/push-update.sh F:/LinOS/build/lineage-19.1-20230508-UNOFFICIAL-crosshatch.zip

这里我有个报错:Error: UNIQUE constraint failed: updates.download_id 是sqlite的报错,可能的原因是不可重复字段冲突。
查看了下脚本中 download_id的 来源 :
echo "$zip_name" | sha1sum | cut -d' ' -f1
发现是zip_name进行哈希,所以猜测可能是我的文件名和我之前推送的是一样的,导致有重复,所以插入失败。
实际进入 setting - system- updater后,检测到新的安装包,可以直接安装。





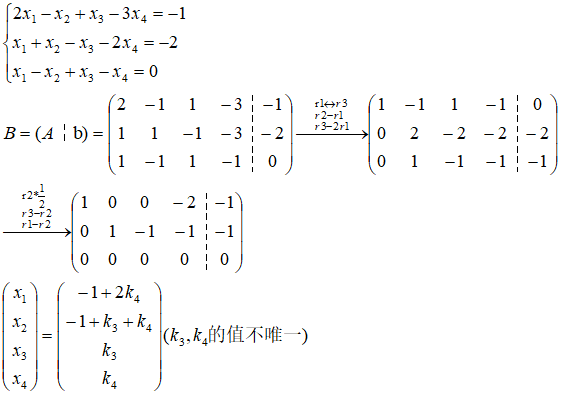






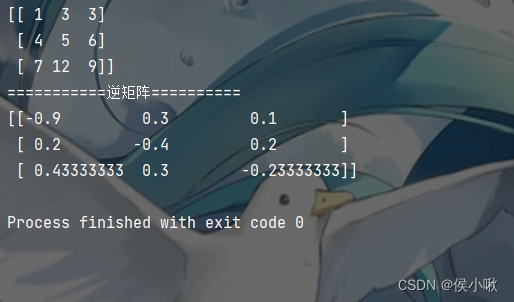






![线性代数[向量]](https://img-blog.csdnimg.cn/35d8c6f2c260420296d2c546a1a08336.png)