- 序列密码体制
- 引言Vernam(弗纳姆)密码技术
- 1917年美国电话电报公司的GilbertVernam为电报通信设计了一种十分方便的密码技术。后来称之为Vernam密码技术.
- 它是一种代数密码技术:其加密方法是,将明文和密钥分别表示成二进制序列,再把它们按位进行模2加法。
- 设明文m= m1m2…,密钥k= k1k2…,其中mi,ki∈GF(2),i≥1,则密文c= c1c2…,其中ci= mi ⊕ki。这里 ⊕为模2加法。
- 由模2加法的性质可知,Vernam密码技术的解密方法和加密方法一样,只是将明文和密文的位置调换一下:mi = ci ⊕ki。
- 例:
- 设明文m=01100001,密钥k=01001110,使用Vernam密码加密求密文。
- 解:加密得:
- c=m⊕k=01100001⊕01001110=00101111
- 设密文c=00101111,密钥k=01001110,使用Vernam密码解密,求密文。
- 解:解密得:
- m=c⊕k=00101111⊕01001110=01100001
- 密码学中的随机数
- 随机数
- 关于随机数,在不同的领域或从不同的角度有许多不同的说法。目前,通常所讲的随机数是指没有规律的数据。
- 随机数的性质
- 随机性
- 随机数在密码学的应用中的无规律性,主要体现在:
- ①具有均匀分布、总体良好的随机统计特征,能通过均匀性检验、独立性检验、游程检验等基本的统计特性检验;
- ②不能重复产生,即在完全相同的条件下,将得到两个不相关的随机序列。
- 不可预测性
- 不可预测性是指即使给出的产生序列的硬件和所有以前产生序列的全部知识,也不能预测下一个随机位是什么,因而随机序列是非周期的。在实际的双向认证或会话密钥产生等的应用中,不仅要求随机序列具有随机性,还要求对序列中的数是不可预测的。
- 随机性
- 随机数的生成方法
- 物理方法
- 是指利用自然界的一些真的随机物理量来生成随机数。比如,放射性衰变、电子设备的噪声、宇宙射线的触发时间等。一般来说,用物理方法得到的随机数具有很好的随机性,但是由于具有的不可重复性,使得统计模拟和验证十分困难。此外,该方法产生随机数的速度和物理随机数发生器的稳定性也使得此方法的应用受到限制。


- 是指利用自然界的一些真的随机物理量来生成随机数。比如,放射性衰变、电子设备的噪声、宇宙射线的触发时间等。一般来说,用物理方法得到的随机数具有很好的随机性,但是由于具有的不可重复性,使得统计模拟和验证十分困难。此外,该方法产生随机数的速度和物理随机数发生器的稳定性也使得此方法的应用受到限制。
- 数学方法
- 这类方法由一个初始状态(称为“种子”)开始,通过一个确定的算法来生成随机数。一旦给定算法和种子,输出的序列就是确定了的,因而产生的序列具有周期性、规律性和重复性,不是真正的随机数,而是伪随机数 (Pseudo Random Numbaer,PRN),产生伪随机数的算法或硬件一般称之为伪随机数生成器(Pseudo Random NumbaerGenerator, PRNG)。PRNG是一个生成完全可预料的数列(称为流)的确定性程序。




- 这类方法由一个初始状态(称为“种子”)开始,通过一个确定的算法来生成随机数。一旦给定算法和种子,输出的序列就是确定了的,因而产生的序列具有周期性、规律性和重复性,不是真正的随机数,而是伪随机数 (Pseudo Random Numbaer,PRN),产生伪随机数的算法或硬件一般称之为伪随机数生成器(Pseudo Random NumbaerGenerator, PRNG)。PRNG是一个生成完全可预料的数列(称为流)的确定性程序。
- 物理方法
- 随机数
- 序列密码的基本原理
- 思想起源


- 设明文为m=m1m2… mi∈GF(2), i>0
- 设密钥为k=k1k2… ki∈GF(2), i>0
- 设密文为c=c1c2… ci∈GF(2), i>0
- 则加密变换为ci= mi + ki (mod 2) i>0
- 则解密变换为mi= ci+ ki (mod 2) i>0
- 序列密码体制的概念
- 序列密码算法(也称为流密码算法)将明文逐位(字节也可以)转换成密文,序列密码体制模型如图所示。

- 在序列密码中,明文按一定长度分组后表示成一个序列,称为明文流(序列中的每一项称为明文字)。
- 加密时,先由种子密钥(或称为主密钥)通过密钥流产生器产生一个密钥流序列,该序列的每一项和明文字具有相同的比特长度,称为密钥字;然后依次把明文流和密钥流中的对应项做二元加法运算(异或运算),产生相应的密文字,由密文字构成密文流输出。
- 解密过程是将同样的密钥流与密文流中的对应项做二元加法运算,恢复出原来的明文流。

- 序列密码算法(也称为流密码算法)将明文逐位(字节也可以)转换成密文,序列密码体制模型如图所示。
- 思想起源
- 序列密码体制的分类
- 同步序列密码(OFB、CTR)
- 在同步序列密码中,密钥流独立于消息流产生

- 在同步序列密码SSC(SynchronousStream Cipher)中,密钥流独立于消息流而产生,一个错误传输只会影响一个符号,不影响后面的符号。
- 优点
- 无错误传播,容易检测插入、删除、重播等主动攻击。
- 缺点
- 一旦接收端和发送端的种子密钥和内部状态不同步,解密就会失败,两者必须立即借助外界手段重新建立同步。
- 特点
- 同步
- 在一个同步序列中,发送方和接收方必须是同步的,即用同样的密钥且该密钥操作在同样的位置(状态),才能保证正确的解密。
- 无错误传播
- 在传输期间,一个密文字(或位)被改变(不是删除和插入)只能影响该密文字(或位)的恢复,不会对后续密文字(或位)产生影响。
- 主动攻击破坏同步
- 按照同步要求,一个主动攻击对密文进行插入、删除或重放操作都会立即破坏其同步,从而可能被解密器检测出来。作为无错误传播的结果,主动攻击者可能有选择地对密文进行改动,并准确地知道这些改动对明文的影响,这时可以采用为数据源提供认证并保证数据完整性的技术。
- 同步
- 举例

- 在同步序列密码中,密钥流独立于消息流产生
- 自同步序列密码(CFB)
- 自同步序列密码也称为异步流密码,其密钥流的产生不是独立于明文流和密文流的,与种子密钥和其前面已产生若干密文字有关。

- 自同步流密码SSSC(Self-SynchronousStream Cipher),密钥流的产生于明文流和密文流
- 优点是即使接收端和发送端不同步,只要接收端能连续地正确地接受到n个密文符号,就能重新建立同步。因此自同步流密码具有有限的差错传播,且分析较同步流密码的分析困难得多

- 特点
- 自同步
- 自同步的实现依赖于密文字被删除或插入,这是因为解密只取决于先前固定数量的密文字。自同步序列密码在同步丢失后能够自动重新建立同步,并正确地解密,只有固定数量的明文字不能解密。
- 有限的错误传播
- 因为自同步序列的状态取决于t个已有的密文字符,若一个密文字(或位)在传输过程中被修改(插入或删除),则解密时最多只影响到后续 t个密文字的解密,即只发生有限的错误传播。
- 难检测主动攻击
- 相比于同步,自同步使得主动攻击者发起的对密文字的插入、删除、重放等攻击只会产生非常有限的影响,正确的解密能很快自动重建。因此,主动攻击对自同步序列密码很困难的,可能需要采用为数据源提供认证并保证数据完整性的技术。有限的错误传播特性使得主动攻击者对密文字的任何改动都会引起一些密文字解密出错。
- 密文统计扩散
- 每个明文字都会影响其后的整个密文,即密文的统计特性被扩散到密文中。所以,自同步序列密码体制在抵抗利用明文冗余度而发起的攻击方面要强于同步序列密码。
- 举例

- 自同步
- 自同步序列密码也称为异步流密码,其密钥流的产生不是独立于明文流和密文流的,与种子密钥和其前面已产生若干密文字有关。
- 密钥流序列的性质
- 极大的周期
- 良好的统计特性
- 抗线性分析
- 抗统计分析
- 序列密码与分组密码的比较
- 分组密码是以一定的固定长度的分组作为每次处理的基本单元;而序列密码则是以一个元素(一个字符或一个比特位)作为基本处理单元。
- 分组密码使用的是一个不随时间变化的固定变换,具有扩散性好、插入敏感等优势,其缺点是加密处理速度慢,存在错误传播;而序列密码是用的一个随时间变换的加密变换,具有传播速度快、低错误传播和硬件实现电路简单等优势,其缺点是低扩散(意味着混乱不够)、插入及修改不敏感。
- 同步序列密码(OFB、CTR)
- 线性反馈寄存器
- 线性移位和非线性寄存器是序列密码产生密钥流的一个组成部分.
- 移位寄存器是指有n个寄存器(称为n-级移位寄存器)r1,r2,…,rn从右到左排列,每个寄存器中能存放1位二进制数,所有寄存器中的数可以统一向右(或向左)移动1位,称为进动1拍. 即r1的值(b1)右移1位后输出,然后r2的值(b2)送r1, r3的值(b3)送r2,……最后, rn的值(bn)送rn-1.

- 基于移位寄存器的序列密码算法
- 反馈移位寄存器(feedback shift register,FSR)
- 是由n位的寄存器和反馈函数(feedback function)组成,如下图所示,n位的寄存器中的初始值称为移位寄存器的初态.
- 工作原理
- 移位寄存器中所有位的值右移1位,最右边的一个寄存器移出的值是输出位,最左边一个寄存器的值由反馈函数的输出值填充,此过程称为进动1拍. 反馈函数f是n个变元(b1,b2,…,bn)的布尔函数. 移位寄存器根据需要不断地进动m拍,便有m位的输出,形成输出序列o1,o2,…,om .

- 移位寄存器中所有位的值右移1位,最右边的一个寄存器移出的值是输出位,最左边一个寄存器的值由反馈函数的输出值填充,此过程称为进动1拍. 反馈函数f是n个变元(b1,b2,…,bn)的布尔函数. 移位寄存器根据需要不断地进动m拍,便有m位的输出,形成输出序列o1,o2,…,om .
- 在图中,每一存储器称为移位寄存器的一级,在任一时刻,这些级的内容构成该反馈移位寄存器的状态,每一状态对应于GF(2)上的一个n维向量,共有2^n 种可能的状态。每一时刻的状态可用n长序列“a1,a2,…,an”的n维向量“(a1,a2,…,an)”来表示,其中ai 是第i 级存储器的内容。

- 初始状态由用户确定,当第i个移位时钟脉冲到来时,每一级存储器ai都将其内容向下一级ai-1传递,并计算f(a1,a2,…,an)作为下一时刻的an。
- 反馈函数f(a1,a2,…,an)是n元布尔函数,即n个变元a1,a2,…,an 可以独立地取0和1两个可能的值,函数中的运算有逻辑与、逻辑或、逻辑补等运算,最后的函数值也为0或1。
- 例:


- 基于移位寄存器的序列密码算法
- 线性反馈移位寄存器LFSR(linear feedback shift register)的反馈函数为线性函数
- 作为密钥流的序列{ai}的周期一定要大,否则密钥流的空间太小,利用穷举搜索可以得到密钥流{ai}
- n级LFSR输出的序列的周期r不依赖于寄存器的初始值,而依赖于特征多项式p(x)
- 如果f(a1,a2,…,an)是(a1,a2,…,an)的线性函数,则称之为线性反馈移位寄存器LFSR(linear feedback shift register),否则称为非线性移位寄存器。此时f 可写为:

- 其中常数ci=0或1,⊕是模2加法。ci=0或1可用开关的断开和闭合来实现,如图所示,这样的线性函数共有2^n个。

- 在线性反馈移位寄存器中总是假定c1,c2,…,cn中至少有一个不为0,否则f(a1,a2,…,an)=0,这样的话,在n个脉冲后状态必然是00…0,且这个状态必将一直持续下去。若只有一个系数不为0,设仅有cj不为0,实际上是一种延迟装置。一般对于n级线性反馈移位寄存器,总是假定cn=1。
- n级线性反馈移位寄存器的状态周期小于等于2^n-1。输出序列的周期与状态周期相等,也小于等于2^n-1。只要选择合适的反馈函数便可使序列的周期达到最大值2^n-1
- 特点
- n级LFSR输出的序列的最大周期是2^n-1
- LFSR的寄存器状态遍历2n-1个非零状态
- 初始状态为全零,则输出序列为0的循环
- 定义 当LFSR的寄存器状态遍历2^n-1个非零状态时,序列的周期达到最大2^n-1,这种序列被称为m序列。
- 本原多项式
- 若n次不可约多项式p(x)的阶为2n-1
- {ai}是周期为2n-1的m-序列的充要条件是其特征多项式f(x)为n阶本原多项式
- 例:

- 序列的周期性

- 反馈移位寄存器(feedback shift register,FSR)
- 常用的序列密码算法
- RC4序列密码算法
- RC4是美国RSA数据安全公司1987年设计的一种序列密码,广泛应用于SSL/TLS标准等商业密码产品中,是目前所知应用最广泛的对称序列密码算法。该算法以OFB方式工作,密钥流与明文相互独立。RSA数据安全公司将其收集在加密工具软件BSAFE中。最初并没有公布RC4的算法,人们通过软件进行逆向分析得到了算法,在这种情况下,RSA数据安全公司于1997年公布了RC4密码算法。
- RC4与基于LFSR的序列密码不同,它是以随机置换为基础、基于非线性数据表变换的序列密码,面向字节操作。它以一个足够大的数据表为基础,对表进行非线性变换,产生非线性的密钥序列。
- RC4使用了256个字节的S表和两个指针(I和J),算法步骤为:
- Step1:初始化S表
- 初始化过程如下:
- (1)对S表进行填充,即令S[0]=0, S[1] =1, S[2]=2, … , S[255]=255
- (2)用密钥k(k[0], k[1], … , k[len(k )]-1])填充另一个256字节的R表。若密钥的长度小于R表的长度,则依次重复填充,直至将R表填满R[i]=k[i mod len( k )]
- (3)J=0;
- (4)对于I=0: 255,重复以下操作:
- {
- J=(J+S[I]+R[I]) mod 256;
- 交换S[I]和S[J]
- }
- {
- RC4算法的优点
- 算法简单、高效,特别适合软件实现。目前,RC4所用的初始密钥至少为128位。RC4被广泛应用于商业密码产品中,例如已经用于Microsoft Windows、Lotus Notes和Oracle的SQL数据库中、为网络浏览器和服务器之间的通信定义的安全套接字层(Secure Socket Layer, SSL);还用于无线系统以及保护无线连接的安全,如应用于IEEE802.11无线LAN标准的WEP(Wired Equivalent Privacy)协议和Wi-Fi保护访问协议等。
- RC4代码实现
- 密钥流:RC4算法的关键是根据明文和密钥生成相应的密钥流,密钥流的长度和明文的长度是对应的,也就是说明文的长度是500字节,那么密钥流也是500字节。当然,加密生成的密文也是500字节,因为密文第i字节=明文第i字节^密钥流第i字节;
- 状态向量S:长度为256,S[0],S[1].....S[255]。每个单元都是一个字节,算法运行的任何时候,S都包括0-255的8比特数的排列组合,只不过值的位置发生了变换;
- 临时向量T:长度也为256,每个单元也是一个字节。如果密钥的长度是256字节,就直接把密钥的值赋给T,否则,轮转地将密钥的每个字节赋给T;
- 密钥K:长度为1-256字节,注意密钥的长度keylen与明文长度、密钥流的长度没有必然关系,通常密钥的长度取为16字节(128比特)。
- 本原多项式

- RC4序列密码算法
- 引言Vernam(弗纳姆)密码技术
应用密码学(张仕斌)第五章
article/2025/11/3 1:56:09
相关文章
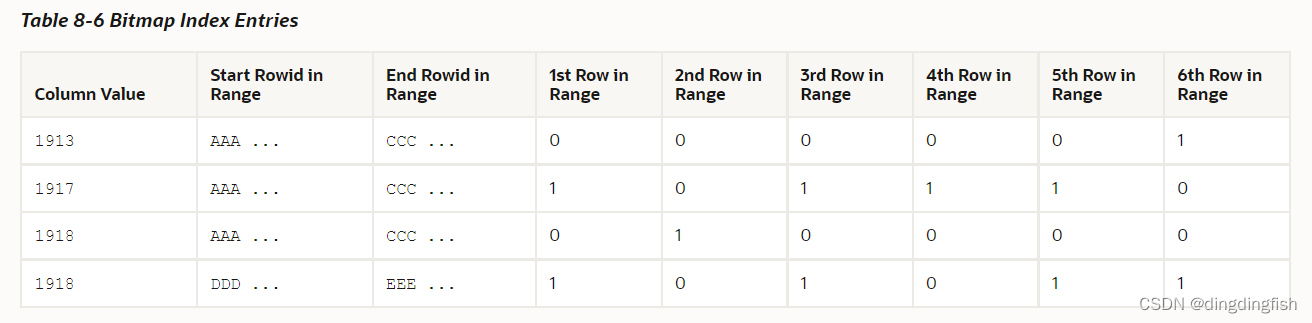
SQL调优指南笔记8:Optimizer Access Paths
本文为SQL Tuning Guide第8章“优化访问路径”的笔记。
重要基本概念 access path The means by which the database retrieves data from a database. For example, a query using an index and a query using a full table scan use different access paths. 数据库从数据库…
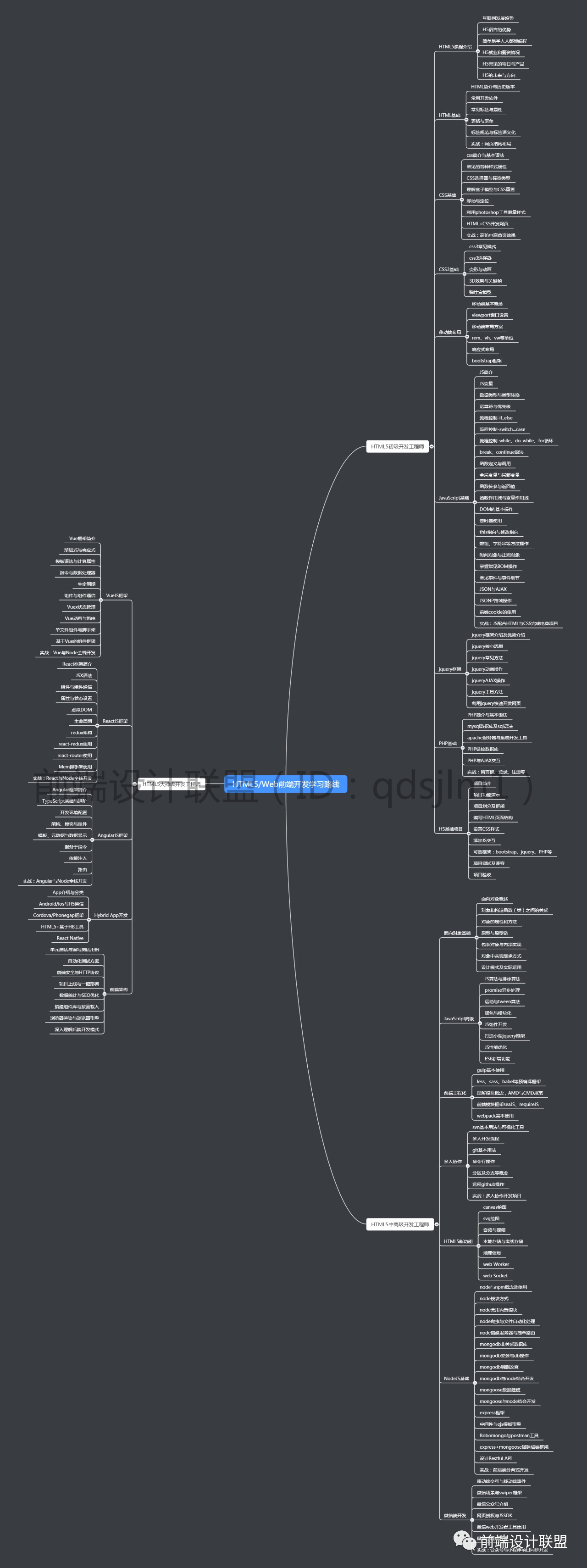
2023年还在问前端怎么学?一份前端学习指南
🍭 Hello,我是爱吃糖的范同学 因为疫情摆烂了许久,学校里又有许多大大小小的烦心事要处理(特别是作业和期末考试😫),所以在博客文章的更新上很长一段时间都没有输出很正经的文章了,…
【前端圭臬】一:写给入坑前端的你
专栏目录
导论
【前端圭臬】一:写给入坑前端的你
HTML 篇
【前端圭臬】二:你知道的和不知道的 HTML
CSS 篇
【前端圭臬】三:详解 CSS 选择器 【前端圭臬】四:CSS 核心机制——如何确定一个属性的值? 【前端圭臬】…
前端什么知识点最难学?
这个最就很难判断,每个人的理解程度不一致,但有两种人,觉得难的他还没学会,会的不觉得难,但是前端不一样了,会了也难,因为谁都对前端提点建议(啥也不懂的老板、产品经理、项目经理、…
【前端】一个好看的前端页面
序言 突发奇想,看到这个特效还不错,就加工了一下,如果也能帮到你,很开心 先上效果图 部分代码讲解
前端生成uuid
function getUUID(len, radix) {var chars 0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz.s…
从零学前端第一讲:前端开发是什么?给初学者有什么建议?
这里是修真院前端小课堂,本篇分析的主题是
【从零学前端第一讲:前端开发是什么?给初学者有什么建议?】 初识前端
1、前端开发是什么?
2、前端开发有前途吗?
3、前端开发哪里学?
4、前端发展…
web 前端入坑第一篇:web前端到底是什么?有前途吗
web前端到底是什么? 某货: “前几年前端开发人员鱼目混杂,技术参差不齐,相对学习起来不规范,导致> 前端开发人员聚集,所以现在前端工种和工资还是没得到普遍重视,但近2年来,> …
前端工程化详解——理解与实践前端工程化
前言: 前端工程化一直是一个老生常谈的问题,不管是面试还是我们在公司做基建都会经常提到前端工程化,那么为什么经常会说到前端工程化,并没有听过后端工程化、Java工程化或者Python工程化呢?我们理解的前端工程化是不是…
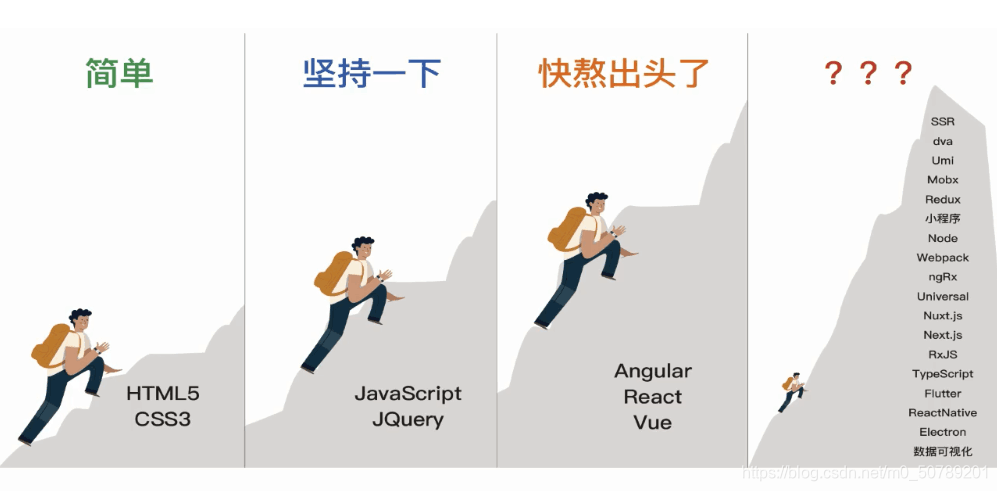
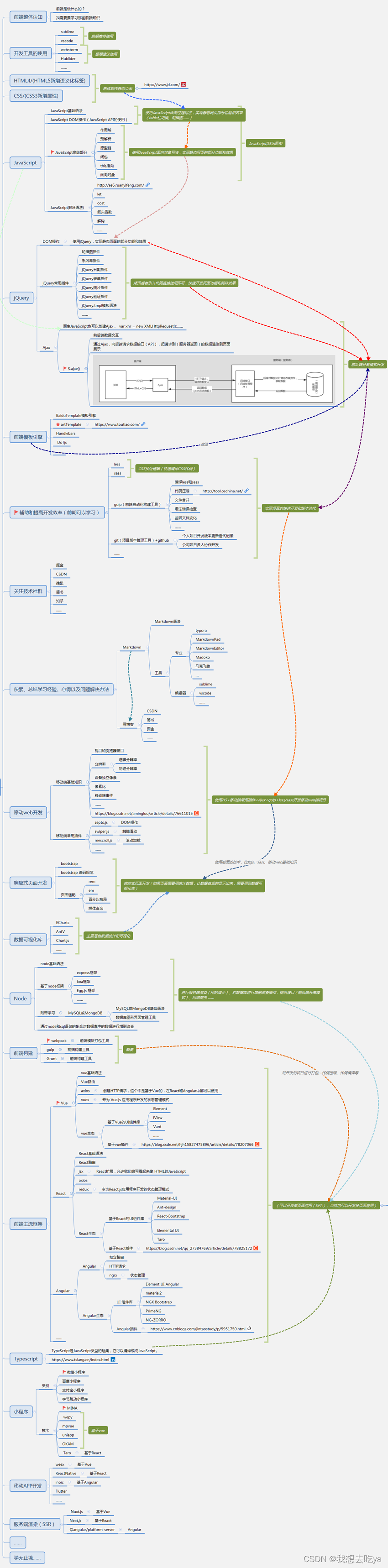
适合我的前端学习路线(学习前端不迷路)
适合我的前端学习路线(学习前端不迷路) 小伙伴们想学习前端,但是却不知如何入手,上网查前端学习路线,第一页往往充斥着各种培训公司的广告,又或者是搜前端学习路线图时,出现大量的路线图导致你还…
前端工程师行业现状怎么样?前景如何?
前端工程师行业现状怎么样?前景如何?前端即网站前台部分,运行在PC端移动端等浏览器上展现给用户浏览的网页。前端市场远没有饱和,现在的市场状况需求量非常多薪资可观。小编将通过官方数据宏观的给大家分析一下前端这个行业。
一…
快毕业了,很多人都不推荐做前端,前端业内最真实情况是什么样的?
偶尔出现这样一种说法,前端热度已经降低了,前端市场已经饱和了,前端工作没有那么好找了。
部分事实确实如此,大概是在2014-2018年,那时候前端技术刚刚崛起,相对来讲工作较现在更容易找到。
随着前端技术的发展及人才需求结构的成熟,现在已经不是会做动态网页就能找到工…
传智教育|一文读懂什么是前端?未来前景怎么样?(附前端学习路线图)
互联网高薪岗位众多,之前被大家津津乐道的后端工程师似乎慢慢不吃香了,原因是:过于内卷。
而为了打破目前内卷的局面,很多小伙伴在转行的时候就开始考虑起了前端工程师,这个岗位相比起后端的学习来说,难度…
我适不适合学前端?看完老程序员的这篇文章给你答案
什么是前端?什么又是后端呢?
1,在你机子上(PC端/手机端)看到的界面,安装的程序。给用户看的、操作的就是前端。你看不到的,帮你保存网络游戏数据,保存应用数据,处理数据的就是后端(服务端)。
2, 目前一般来说,前端指的就是浏览器端,后端指的就是直接为浏览器端…
关于根轨迹对于控制系统的一点理解
自动控制理论根轨迹的学习过程中,经常会遇到几个问题:
为什么要用根轨迹法?为什么根轨迹法最终转化为调整增益K来反应系统的稳定性和动态性能?为什么根轨迹法用开环传递函数求解的却是闭环极点?
盲目的借助于matlab进…
4.4 绘制根轨迹的MATLAB函数
4.4.1 rlocus ⒈.功能:绘制系统的根轨迹。 ⒉.格式:
[r,k]rlocus(n,d) [r,k]rlocus(g) [r,k]rlocus(n,d,k) [r,k]rlocus(g,k) ⒊.说明:
rlocus 函数可计算出或画出SISO系统的根轨迹,其中g(或n,d)为对象模型,输入变量…