分位数回归简介

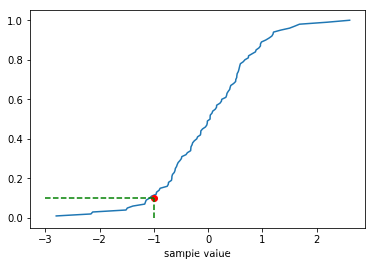
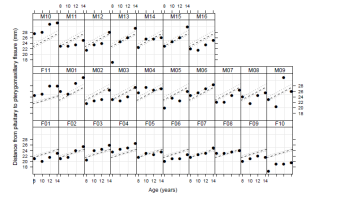
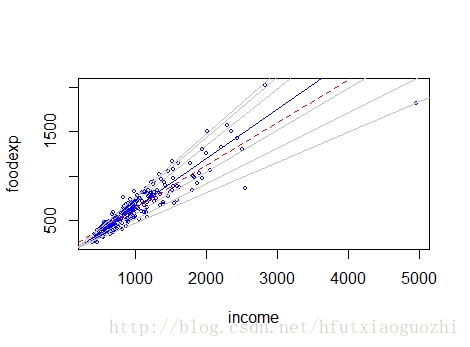
简介参照可参照参考文献【1】。如下图，散点图代表我们所需分析数据，若用简单的参数方程拟合，即只利用期望值，会损失很多数据特征。因此分位数回归就可以乘风破浪了。

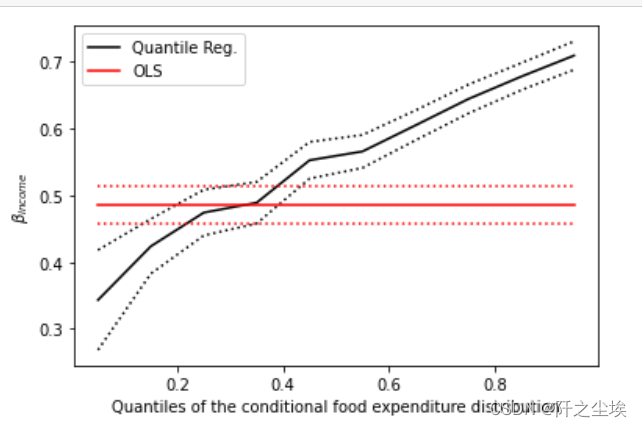
分位数数回归的形式为不同分为数对应一条回归曲线。本文中均以90th分位数为例，其它分位数均可类比得出。

分为数是通过样本到回归曲线的垂直距离的加权和求得。即红线（下图）下方的数据占总体的90%。

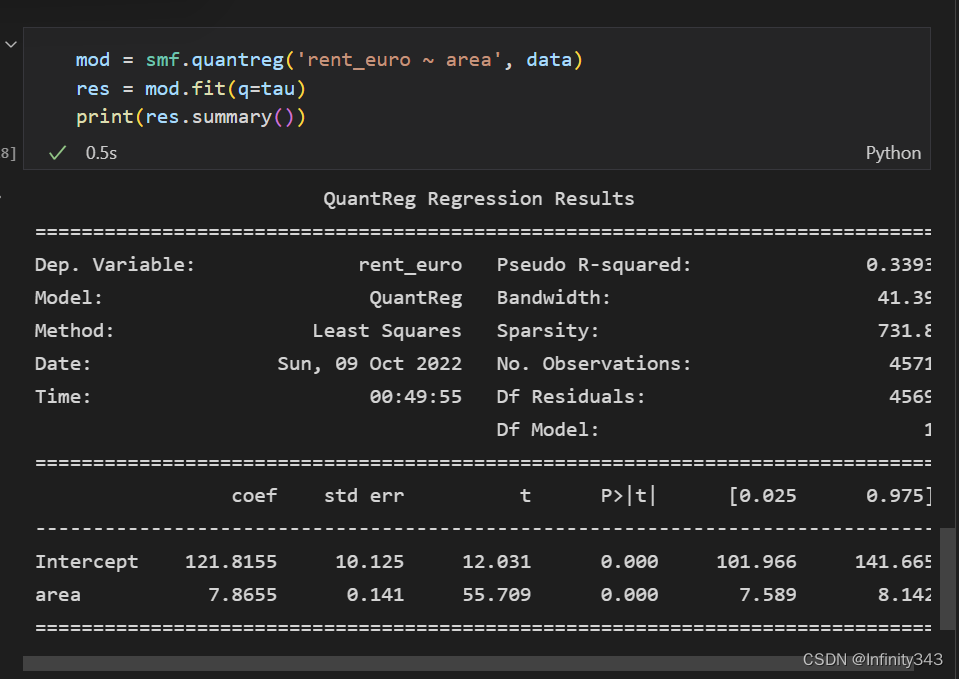
实现方法

MATLAB: quantreg
R package:quantreg

以matlab为例，上图的代码如下，

x=(1:1000)';
y=randn(size(x)).*(1+x/300)+(x/300).^2;
[p,stats]=quantreg(x,y,.9,2);
scatter(x,y)
hold on
plot(x,polyval(p,x),x,stats.yfitci,'k:')
legend('data','2nd order 90th percentile fit','95% confidence interval','location','best')

参考文献

【1】https://blog.csdn.net/buracag_mc/article/details/90729314