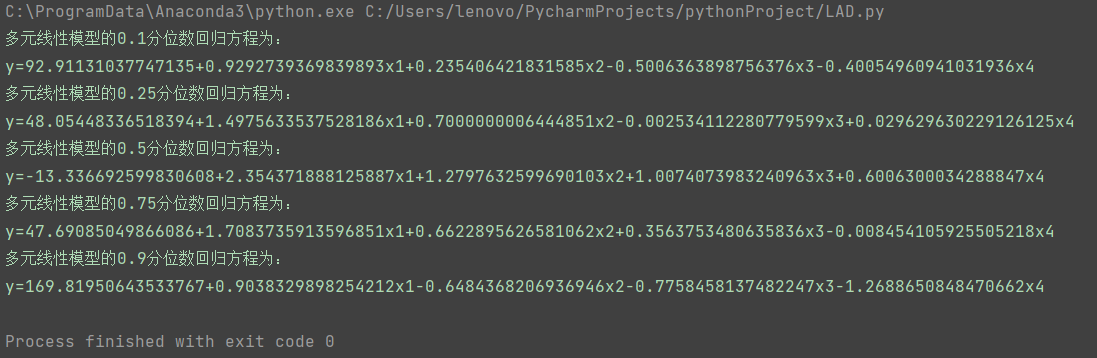
偶尔在机器学习的论文中了解到了分位数回归，发现这个方法应用也满广的。

1. 分位数回归的数学原理

一般的回归方法是最小二乘法，即最小化误差的平方和：

$$\min \sum (y_i-{\hat{y}}_i{)}^2$$

其中，$y_i$ 是真实值，而 ${\hat{y}}_i$ 是预测值。而分位数的目标是最小化加权的误差绝对值和：

$$\underset{{\hat{y}}_i}{\min }\sum _{y_i\ge {\hat{y}}_i}\tau |y_i-{\hat{y}}_i|+\sum _{y_i<{\hat{y}}_i}(1-\tau )|y_i-{\hat{y}}_i|$$

其中， $\tau$ 是给定的分位数。决策变量是 ${\hat{y}}_i$，可以证明，使上面表达式最小化的 ${\hat{y}}_i$ 就是给定分位数 $\tau$ 对应的分位点（将上面式子转化为连续密度函数的积分，然后求一阶导数即可证明）。

上式也可以简写成：
$$\underset{{\hat{y}}_i}{\min }\sum \left[\tau (y_i-{\hat{y}}_i{)}^{+}+(1-\tau )({\hat{y}}_i-y_i{)}^{+}\right]$$

2. 分位数回归的求解原理

为了求出分位数的回归方程，假设 ${\hat{y}}_i={\mathbf{X}}_{\mathbf{i}}\mathbf{\beta }$，那么求解的目标函数转化为：

$$\underset{\mathbf{\beta }\in {\mathbb{R}}^k}{\mathrm{argmin}}\sum \left[\tau (y_i-{\mathbf{X}}_{\mathbf{i}}\mathbf{\beta }{)}^{+}+(1-\tau )({\mathbf{X}}_{\mathbf{i}}\mathbf{\beta }-y_i{)}^{+}\right]$$

决策变量为 $k$ 维回归方程的参数向量 $\mathbf{\beta }$。在实际的求解中，将上式转化为一个线性规划问题，引入两个虚拟变量 $u_i^{+}$，$u_i^{-}$：

$$\begin{array}{rlrl}& \underset{\mathbf{\beta }\in {\mathbb{R}}^k}{\mathrm{argmin}}& & \sum \left[\tau u_i^{+}+(1-\tau )u_i^{-}\right]\\ & s.t.& & i=1,2,\dots ,n\\ & & & y_i={\mathbf{X}}_{\mathbf{i}}\mathbf{\beta }+u_i^{+}-u_i^{-}\\ & & & u_i^{+}\ge 0,u_i^{-}\ge 0\end{array}$$

然后用单纯形法或内点法求解，就能得出分位数回归方程（python 与 R 软件求出的分位数回归方程可能略微不同，因为求解方法不一样, python 使用了迭代的加权最小二乘法求解）。

3 python 分位数回归

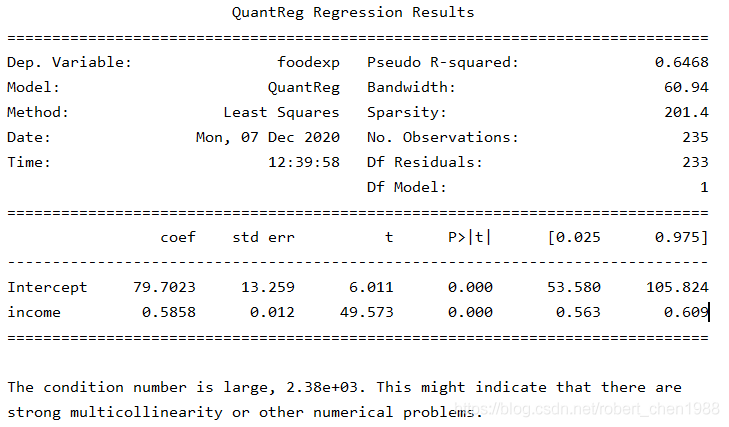
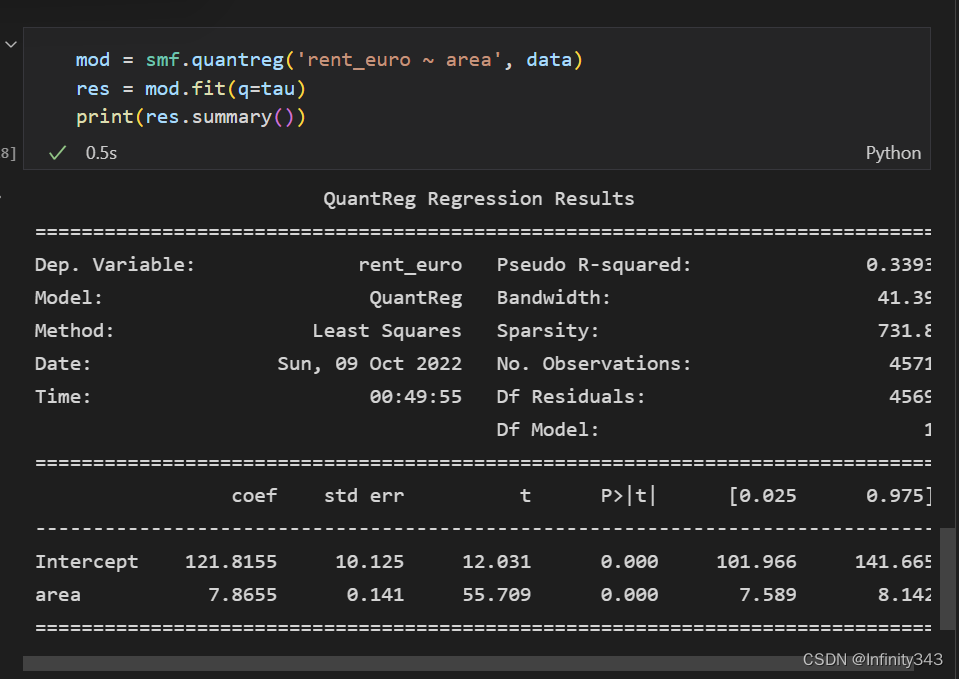
分位数回归要用到 statsmodels，下面的代码得到分位数为 0.6 的回归方程，并画图：

import statsmodels.formula.api as smf
import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as pltdata = sm.datasets.engel.load_pandas().data
mod = smf.quantreg('foodexp ~ income', data)
res = mod.fit(q=0.6)
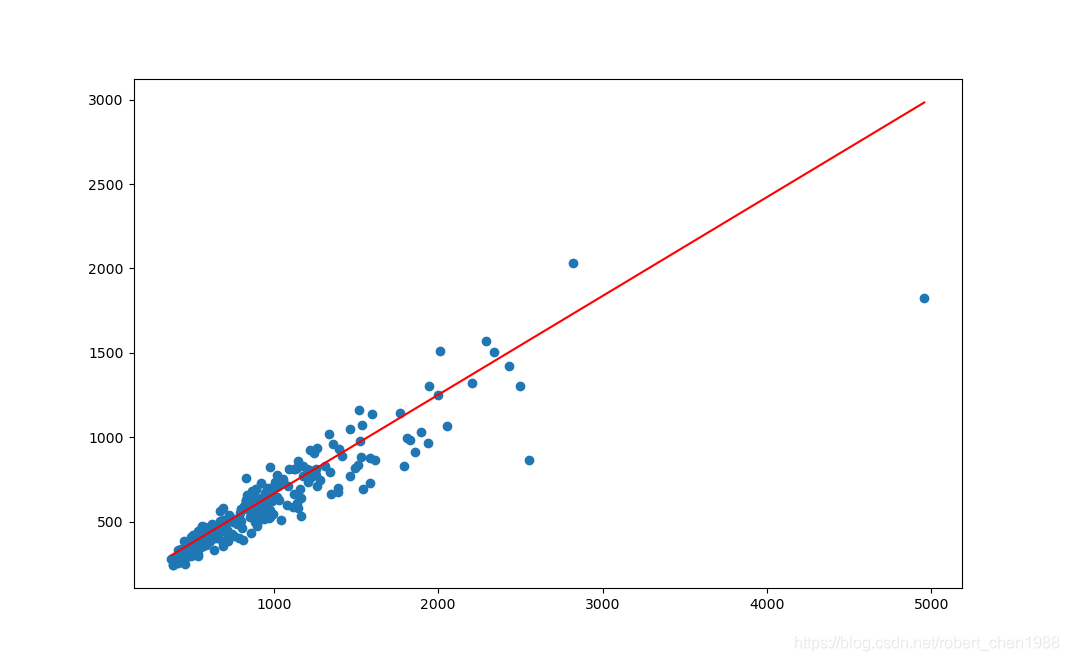
print(res.summary())plt.scatter(data['income'], data['foodexp'])
xx = np.arange(min(data['income']), max(data['income']))
yy = [i*res.params['income'] + res.params['Intercept'] for i in xx]
plt.plot(xx, yy, color='red')
plt.show()

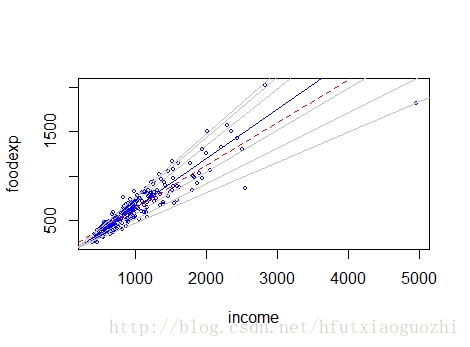
输出结果：

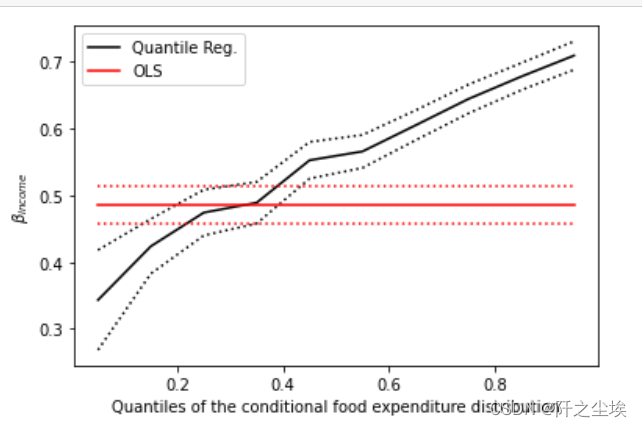
回归方程就是上面的红线，它将 40% 的数据分割在上面，60% 的数据分割在下面。

转载于个人公众号：Python 统计分析与数据科学