多元线性模型的分位数回归
- 一、为什么要使用分位数回归?
- 二、分位数回归基本模型
- 三、分位数回归估计--线性规划
- 3.1损失函数
- 3.2目标函数
- 3.3线性规划
- 3.4回归算法
- 四、实际案例分析与python编程计算
- 4.1引入数据集
- 4.2计算 β ^ \widehat{\beta} β
- 五、参考文献
一、为什么要使用分位数回归?
众所周知,对于线性模型 Y = X β + ε Y=X\beta+\varepsilon Y=Xβ+ε,人们往往习惯于使用均值回归。但是均值回归往往更关注的只是均值,对于数据的“其他部位”往往照顾不够。有时不能较为客观地反映一组数据的各个层次的实际情况。比如我是一名还在读大三的本科生,我和当前的世界首富埃隆▪马斯克人均财富千亿美元级别,显然这个均值对于反映我的财富水平来说是毫无意义的,甚至是有信息误导的作用。但是如果试想使用分位数回归,那我就可以避免被马斯克平均了。
我们知道在均值回归的普通最小二乘法中,我们是通过求残差的平方和最小来估计参数的。而在分位数回归中我们通常求残差的绝对值的加权求和最小来估计参数。就我目前了解,这样做的目的之一是减小离群点的大误差对整体回归估计的影响。例如,通常离群点处的残差是远远大于1的,在这种情况下残差的绝对值就要远小于残差的平方值,所以使用残差的绝对值可以减少离群点处的误差对整体回归的影响,而这也算是我们进行分位数回归的初衷之一。
分位数回归通常是采用最小一乘法,而最小一乘法对误差项 ε \varepsilon ε并没有要求其服从正态分布,所以相比于均值回归通常采用的最小二乘法对误差 ε \varepsilon ε要求服从正态分布来说,最小一乘法的误差 ε \varepsilon ε更具有普遍性。
总的来说相比于均值回归,(1)分位数回归对数据分布的情况掌握的更全面客观。(2)使用分位数回归,离群点对于数据整体的影响要比较使用均值回归小的多。所以我们也可以说分位数回归更加稳健。(3)分位数回归对于误差项更具有普适性。
二、分位数回归基本模型
Y ( θ ) = X β ( θ ) + ε ( θ ) (1) Y^{(\theta)}=X\beta^{(\theta)}+\varepsilon^{(\theta)} \tag{1} Y(θ)=Xβ(θ)+ε(θ)(1)
其中 θ \theta θ为分位数,对于实随机变量 Y Y Y,其右连续分布函数为 F ( y ) = P ( Y ≤ y ) F(y)=P(Y\leq y) F(y)=P(Y≤y), Y Y Y的 θ \theta θ分位数函数为 F − 1 ( θ ) = i n f ( y : F ( y ) ≥ θ ) F^{-1}(\theta)=inf(y:F(y)\ge \theta) F−1(θ)=inf(y:F(y)≥θ),也即第 100 θ % 100\theta\% 100θ%的 y y y。
其中, Y ( θ ) = [ y 1 y 2 ⋮ y n ] , X = [ 1 x 11 ⋯ x 1 p 1 x 21 ⋯ x 2 p ⋮ ⋮ ⋱ ⋮ 1 x n 1 ⋯ x n p ] β ( θ ) = [ β 0 β 1 ⋮ β p ] , ε ( θ ) = [ ε 1 ε 2 ⋮ ε n ] Y^{(\theta)}=\left[ \begin{matrix} y_{1} \\ y_{2} \\ \vdots \\ y_{n} \end{matrix} \right] ,X=\left[ \begin{matrix} 1&x_{11}&\cdots&x_{1p} \\ 1&x_{21}&\cdots&x_{2p} \\ \vdots&\vdots&\ddots&\vdots \\ 1 &x_{n1}&\cdots&x_{np} \end{matrix} \right]\\ \beta^{(\theta)}=\left[ \begin{matrix} \beta_{0} \\ \beta_{1} \\ \vdots \\ \beta_{p} \end{matrix} \right],\varepsilon^{(\theta)}=\left[ \begin{matrix} \varepsilon_{1} \\ \varepsilon_{2} \\ \vdots \\ \varepsilon_{n} \end{matrix} \right] Y(θ)=⎣⎢⎢⎢⎡y1y2⋮yn⎦⎥⎥⎥⎤,X=⎣⎢⎢⎢⎡11⋮1x11x21⋮xn1⋯⋯⋱⋯x1px2p⋮xnp⎦⎥⎥⎥⎤β(θ)=⎣⎢⎢⎢⎡β0β1⋮βp⎦⎥⎥⎥⎤,ε(θ)=⎣⎢⎢⎢⎡ε1ε2⋮εn⎦⎥⎥⎥⎤
三、分位数回归估计–线性规划
3.1损失函数
定义损失函数为 ρ θ ( ε ) = ε ( θ − I ( ε ) ) (2) \rho_{\theta}(\varepsilon)=\varepsilon(\theta-I(\varepsilon))\tag{2} ρθ(ε)=ε(θ−I(ε))(2)
其中,
I ( ε ) = { 0 , ε ≥ 0 1 , ε < 0 (3) I(\varepsilon)= \begin{cases} 0, \varepsilon\ge0 \\ 1, \varepsilon<0 \end{cases}\tag{3} I(ε)={0,ε≥01,ε<0(3)
3.2目标函数
一般地,根据 K o e n k e r ( 1978 ) Koenker(1978) Koenker(1978),对于 θ \theta θ分位数回归,我们的目标函数通常采用如下函数:
min β ∈ R m ∑ i = 1 n ρ θ ( y i − x i ′ β ) (4) \min_{\beta\in R^{m}}\sum_{i=1}^{n}\rho_{\theta}(y_{i}-x_{i}'\beta)\tag{4} β∈Rmmini=1∑nρθ(yi−xi′β)(4)
3.3线性规划
对于式 ( 4 ) (4) (4),我们可以用另一种等价形式表达: min β ∈ R m ∑ i = 1 n [ θ u i + ( 1 − θ ) v i ] (5) \min_{\beta\in R^{m}}\sum_{i=1}^{n}[\theta u_{i}+(1-\theta)v_{i}]\tag{5} β∈Rmmini=1∑n[θui+(1−θ)vi](5)
其中 u i , v i u_{i},v_{i} ui,vi分别是 ( y i − x i ′ β ) (y_{i}-x_{i}'\beta) (yi−xi′β)的正部和负部:
u i = { y i − x i ′ β , y i − x i ′ β ≥ 0 0 , y i − x i ′ β < 0 (6) u_{i}=\begin{cases} y_{i}-x_{i}'\beta, y_{i}-x_{i}'\beta\ge0 \\ \quad\quad\quad0, y_{i}-x_{i}'\beta<0 \end{cases}\tag{6} ui={yi−xi′β,yi−xi′β≥00,yi−xi′β<0(6)
v i = { 0 , y i − x i ′ β ≥ 0 y i − x i ′ β , y i − x i ′ β < 0 (7) v_{i}=\begin{cases} \quad\quad\quad0, y_{i}-x_{i}'\beta\ge0 \\ y_{i}-x_{i}'\beta, y_{i}-x_{i}'\beta<0 \end{cases}\tag{7} vi={0,yi−xi′β≥0yi−xi′β,yi−xi′β<0(7)
我们知道,一个函数等于它的正部 − - −负部,一个函数的绝对值等于它的正部 + + +负部。所以,我们可以得到下面的线性规划:
{ min ∑ i = 1 n [ θ u i + ( 1 − θ ) v i ] x i ′ β + u i − v i = y i β ∈ R m , u i ≥ 0 , v i ≥ 0 , i = 1 , 2 , ⋯ , n (8) \begin{cases} \min\sum_{i=1}^{n}[\theta u_{i}+(1-\theta)v_{i}]\\ x_{i}'\beta+u_{i}-v_{i}=y_{i}\\ \beta\in R^{m},u_{i}\ge0,v_{i}\ge0,i=1,2,\cdots,n \end{cases}\tag{8} ⎩⎪⎨⎪⎧min∑i=1n[θui+(1−θ)vi]xi′β+ui−vi=yiβ∈Rm,ui≥0,vi≥0,i=1,2,⋯,n(8)
对于该线性规划,
{ A = [ X I n − I n ] , B = Y C = [ 0 1 × ( p + 1 ) , θ 1 × n , ( 1 − θ ) 1 × n ] (9) \begin{cases}A=\left[\begin{matrix} X&I_{n}&-I_{n} \end{matrix} \right],B=Y \\ C=[0_{1\times(p+1)},\theta_{1\times n},(1-\theta)_{1\times n}]\end{cases}\tag{9} {A=[XIn−In],B=YC=[01×(p+1),θ1×n,(1−θ)1×n](9)
3.4回归算法
s t e p ( 1 ) step(1) step(1):输入回归数据 X X X和 Y Y Y
s t e p ( 2 ) step(2) step(2):根据 ( 9 ) (9) (9)计算出线性规划的相关矩阵 A , B , C A,B,C A,B,C
s t e p ( 3 ) step(3) step(3):将 A , B , C A,B,C A,B,C带入线性规划算法模块,求得最优解 ( β , u , v ) T (\beta,u,v)^{T} (β,u,v)T
注:关于相关的线性规划算法本文不再赘述。
四、实际案例分析与python编程计算
4.1引入数据集
我们以著名的 H a l d Hald Hald数据为例。
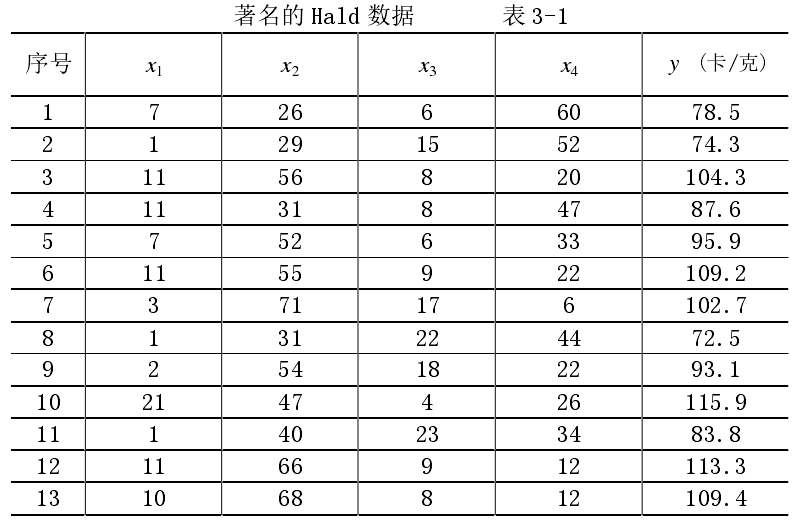
4.2计算 β ^ \widehat{\beta} β
下面给出计算多元线性模型分位数回归方程完整 p y t h o n python python源代码:
import pandas as pd
import numpy as np
from scipy import optimize
#----------------------多元线性模型的分位数回归---------------------------------------------------------#导入数据
dataset1=pd.read_excel('Hald.xlsx')
dataset2=pd.read_excel('Hald.xlsx')#输入分位数theta
theta=[0.1,0.25,0.5,0.75,0.9]
#计算X,Y
Y=dataset1['Y'].values
dataset2['Y']=1
X=dataset2.values#计算A,B
n=len(X)
B=Y
In=np.eye(n)
A=np.hstack((X,In,-In))
p=len(X[0])-1
l=np.ones(n,np.int)
o=np.zeros(p+1,np.int)#给出线性规划的自变量取值范围
b=[]
for i in range(p+1):b.append(((None,None)))
for i in range(2*n):b.append((0,None))#使用optimize包的linprog函数求解线性规划
for i in theta:C = np.hstack((o, i * l, (1 - i) * l))r = optimize.linprog(C,A_eq=A,b_eq=B,bounds=b)x=r.x#计算β估计beta=[]print('多元线性模型的{}分位数回归方程为:\ny='.format(i), end='')for i in range(p+1):beta.append(x[i])print(beta[0], end='')for i in range(1, p + 1):if beta[i] > 0:print('+{}x{}'.format(beta[i], i), end='')else:print('{}x{}'.format(beta[i], i), end='')print('\n',end='')
下面给出程序运行结果:
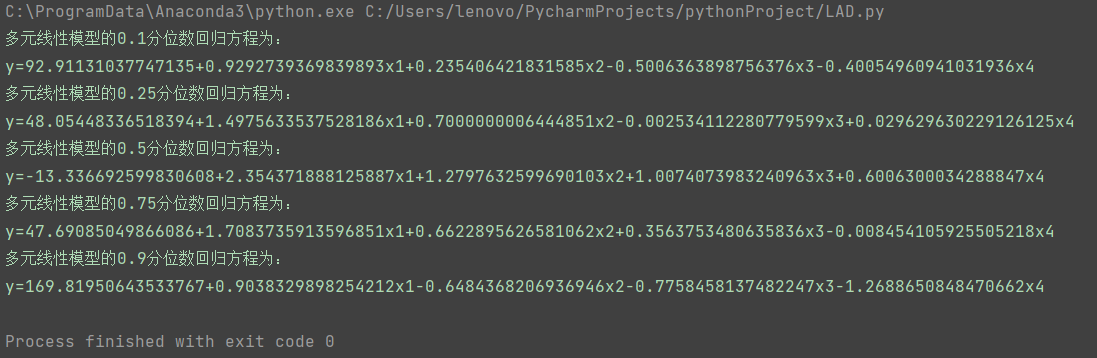
五、参考文献
[1]分位数回归理论及其在金融风险测量中的应用/王新宇著.——北京:科学出版社,2010.6
[2]吕书龙. 最小一乘估计快速算法的研究[D].福州大学,2003.