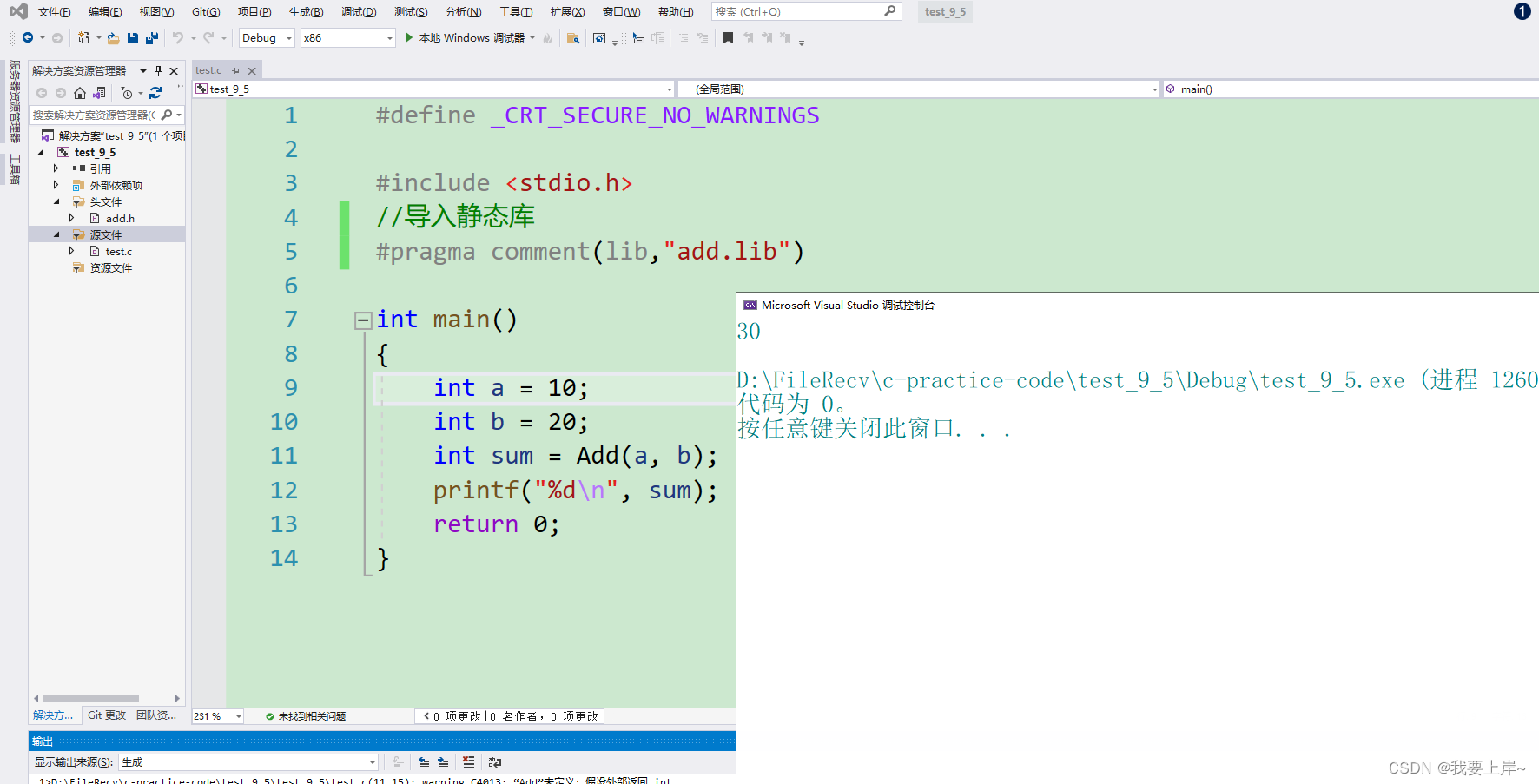
基于分位数回归的成都空气质量指数的数据分析

空气质量指数计算公式为：

$I=\frac{I_{high}-I_{low}}{C_{high}-C_{low}}(C-C_{low})+I_{low}$

（1）线性回归模型得到的是一种条件均值，并未考虑到因变量总体上的分布特征，在需要了解因变量位置（分位数）上的信息时，线性回归就显示出了不足。

（2）线性（均值）回归模型最基本的假设之一正态分布，随机误差且独立时，通过最小二乘法得到的参数估计值是最小方差无偏估计。但是现实生活中大多数数据是不满足正态分布的，这时如果仍然用线性回归模型进行分析，由于在假设检验中值的计算依赖正态性假设，可能会造成值的有偏性，从而导致假设检验无效。若样本数据中存在异方差性或数据的分布是尖峰厚尾的，最小二乘估计量则不具有上述的良好性质。

（3）当样本数据中有离群点存在时，用线性回归模型计算得到的参数估计值可能有较大的偏差，因此，在进行回归拟合时通常会是在去掉离群点后建立线性（均值）回归模型，但这会使离群点在一些社会科学研究中丧失研究意义。

而分位数回归模型相对于一般的线性（均值）回归模型来说，条件更为宽泛，可以描述因变量的全局特征，而不只是均值。另一方面，分位数回归模型具有稳健性，模型的估计值通常不受离群点的影响，从这一角度来说，分位数回归有较强的稳健性。

$Q_{\theta }(y|x)=X^T\beta (\theta )+b(\theta )$

模型检验：

模型显著性检验（Wald检验）、系数的显著性检验（t统计量）、不同分位数模型的联合相等检验、拟合优度检验（R方）

实证分析

对AQI作描述性分析，画出箱线图和QQ图

样本数据中AQI的中位数较小，且有较大的离群点，QQ图为一条曲线且不是对称的，与正态QQ线相差较大，综合来说，样本数据中的AQI并不满足正态分布，而分位数回归模型对数据的分布没有要求，因此可以用分位数回归模型来分析样本数据。

为了消除由于量纲不同对数据的分析结果造成影响，对数据进行归一化处理，将数据固定在了(0,1)范围内。

以PM2.5、PM10、SO2、CO、NO2、O3浓度为自变量，以AQI为因变量，建立分位数分别为0.25、0.50、0.75的位数回归模型（QRM）。

不同分位数回归模型下系数的显著性不同，但基本都是有4个变量对AQI的影响是显著的，并且每个模型中PM2.5浓度对应的系数绝对值最大，说明它对AQI的影响程度最大。

在0.05显著性水平下，只有O3浓度对应的系数在3个模型中是不联合相等的，即在不同的分位数模型中O3浓度对AQI的影响程度不同，不能随意剔除，而其他的变量在0.05显著性水平下是联合相等的，即在不同的分位数回归模型中对AQI影响效果在一定程度上相同，存在剔除的可能。

模型优化：向后剔除法剔除系数不显著的变量。

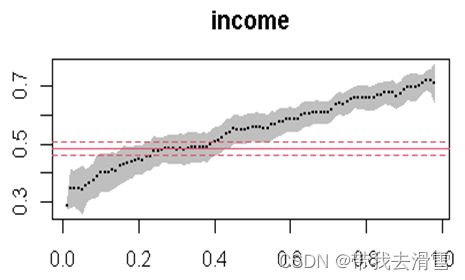
下图描述了在不同分位数水平下的回归模型系数的置信区间，分位数从0.01到0.99上等距变化。图中深色的曲线表示不同分位数水平下各自变量对应的系数估计值，灰色区域表示系数的95%置信区间，深色虚线表示均值回归模型中各系数的估计值，两侧的浅色虚线之间为均值回归模型中系数的95%置信区间。

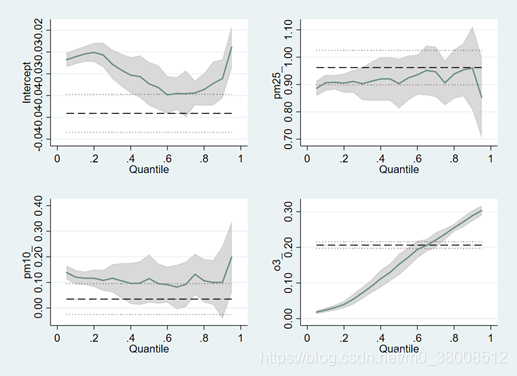
随着分位数的增大，各系数的置信区间在逐渐变宽，O3浓度对应的系数估计值的置信区间先变宽后变窄。系数的置信区间变宽说明系数估计值的标准差在逐渐变大，系数估计值的波动性在增强。以上系数置信区间图中，只有O3浓度对应的系数估计值是具有单调性，不存在“分位数交叉问题”，即在不同的分位数水平下，O3浓度对AQI的影响不同，其余变量在不同分位数水平下对AQI的影响效果在一定程度上相同。另外，除PM2.5浓度对应的系数估计值基本在均值回归模型的系数置信区间内之外，其余系数的估计值基本不在均值回归模型的系数置信区间之内，尤其是低分位数和高分位数上，差别较大，这也进一步说明了均值回归模型在一定程度上具有不合理性，分位数回归模型可以更好地解释变量间的关系。

将1788个样本平均分为3等份，分别为第1-596，597-1192，1193-1788个样本数据。对新组成的3个样本数据重新进行分位数为0.25、0.50、0.75的分位数回归模型。

总结：

线性（均值）回归模型只是通过拟合均值表达数据的集中趋势，无法刻画数据的位置（分位点）上的变化，在满足假设的情况下，线性（均值）回归具有较好的拟合效果，但是分位数回归模型具有较好的稳健性，并且能描述数据不同位置（分位点）上的估计值，当数据不满足假设条件时尤其是数据呈偏态分布时，分位数回归模型拟合效果更好。

部分Stata代码：
*读取数据，数据处理
insheet using E:\计量论文\成都市空气质量指数.csv
rename o3_8h o3
*描述性统计
asdoc sum
*QQ图
qnorm aqi
*箱线图
graph box aqi
*相关系数
asdoc pwcorr aqi pm25 pm10 so2 co no2 o3, star(all) nonum replace
*归一化处理
egen maqi =min(aqi)
egen Maqi =max(aqi)
gen aqi_=(aqi-maqi)/(Maqi-maqi)egen mpm25 =min(pm25)
egen Mpm25 = max(pm25)
gen pm25_=(pm25-mpm25)/(Mpm25-mpm25)egen mpm10 =min(pm10)
egen Mpm10 =max(pm10)
gen pm10_=(pm10-mpm10)/(Mpm10-mpm10)egen mso2 =min(so2)
egen Mso2 =max(so2)
gen so2_=(so2-mso2)/(Mso2-mso2)egen mco =min(co)
egen Mco =max(co)
gen co_=(co-mco)/(Mco-mco)egen mno2 =min(no2)
egen Mno2 =max(no2)
gen no2_=(no2-mno2)/(Mno2-mno2)egen mo3 =min(o3)
egen Mo3 =max(o3)
gen o3_=(o3-mo3)/(Mo3-mo3)*分位数回归
eststo : quietly regress aqi_ pm25_ pm10_ so2_ co_ no2_ o3_
eststo : quietly qreg aqi_ pm25_ pm10_ so2_ co_ no2_ o3_ ,quantile(.25)
eststo : quietly qreg aqi_ pm25_ pm10_ so2_ co_ no2_ o3_ ,quantile(.50)
eststo : quietly qreg aqi_ pm25_ pm10_ so2_ co_ no2_ o3_ ,quantile(.75)
asdoc esttab est2 est3 est4 est5, b p t staraux
*Wald检验
qreg aqi_ pm25_ pm10_ so2_ co_ no2_ o3_ ,quantile(.25)
test pm25_ pm10_ so2_ co_ no2_ o3_
qreg aqi_ pm25_ pm10_ so2_ co_ no2_ o3_ ,quantile(.50)
test pm25_ pm10_ so2_ co_ no2_ o3_
qreg aqi_ pm25_ pm10_ so2_ co_ no2_ o3_ ,quantile(.75)
test pm25_ pm10_ so2_ co_ no2_ o3_
*联合相等检验
sqreg aqi_ pm25_ pm10_ so2_ co_ no2_ o3_,q(.25,.50,.75)
test[q25=q50=q75]:pm25_
test[q25=q50=q75]:pm10_
test[q25=q50=q75]:so2_
test[q25=q50=q75]:co_
test[q25=q50=q75]:no2_
test[q25=q50=q75]:o3_
*向后剔除（最终）
eststo : quietly qreg aqi_ pm25_ pm10_ o3_ ,quantile(.25)
eststo : quietly qreg aqi_ pm25_ pm10_ o3_ ,quantile(.50)
eststo : quietly qreg aqi_ pm25_ pm10_ o3_ ,quantile(.75)
asdoc esttab est1 est2 est3 , b p t staraux
*检验过程代码同上
*稳健性检验（归一化代码同上）
insheet using E:\计量论文\数据1.csv
eststo : quietly qreg aqi1_ pm251_ pm101_ o31_ ,quantile(.25)
eststo : quietly qreg aqi_ pm251_ pm101_ o31_ ,quantile(.50)
eststo : quietly qreg aqi_ pm251_ pm101_ o31_ ,quantile(.75)
asdoc esttab est1 est2 est3 , b p t staraux
insheet using E:\计量论文\数据2.csv
eststo : quietly qreg aqi1_ pm252_ pm102_ o32_ ,quantile(.25)
eststo : quietly qreg aqi_ pm252_ pm102_ o32_ ,quantile(.50)
eststo : quietly qreg aqi_ pm252_ pm102_ o32_ ,quantile(.75)
asdoc esttab est1 est2 est3 , b p t staraux
insheet using E:\计量论文\数据3.csv
eststo : quietly qreg aqi1_ pm253_ pm103_ o33_ ,quantile(.25)
eststo : quietly qreg aqi_ pm253_ pm103_ o33_ ,quantile(.50)
eststo : quietly qreg aqi_ pm253_ pm103_ o33_ ,quantile(.75)
asdoc esttab est1 est2 est3 , b p t staraux