二叉树的前序、中序、后序遍历我想大家应该都很熟悉了，那我们今天就来讲一下二叉树的层次遍历。

二叉树的前序、中序、后序遍历需要用到栈（递归的过程也就是一个栈），层次遍历需要借助队列这个数据结构。

层次遍历的思路

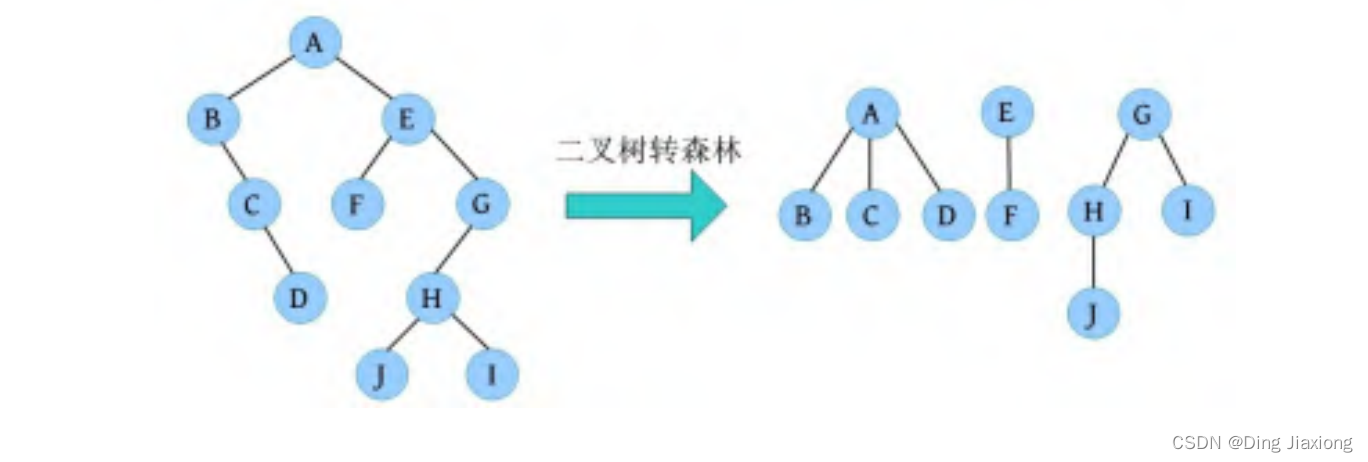
我们给出一个二叉树：

这棵二叉树的层次遍历次序为：A、B、C、D、F、G

以人的思维来看层次遍历貌似比前、中、后序遍历更加简单易懂，但是程序到底如何实现这样的效果呢？这里我们需要用到一个数据结构，那就是队列。

核心思想：每次出队一个元素，就将该元素的孩子节点加入队列中，直至队列中元素个数为0时，出队的顺序就是该二叉树的层次遍历结果。

可能这句话不太好理解，我们依旧是以画图的形式来表达：

1. 初始状态下，队列中只保留根节点的元素：

2. 当A出队时，将A的孩子节点加入队列中：

3.重复上面的动作，队首元素出队时，将孩子节点加入队尾.......

...........

相信看了上面的过程，大家对层次遍历的思路已经有了清晰的认识，那么我们就需要用代码来实现它了：

层次遍历的实现

public class MyTree {public static class TreeNode{public Object key;public TreeNode parent;public List<TreeNode> childrens = new ArrayList<>();public TreeNode(Object key) {this.key = key;}}private int size = 0;private TreeNode root;public MyTree(TreeNode root) {this.root = root;size++;}/*** 层次遍历** @param treeNode* @return*/public List<TreeNode> levelOrder(TreeNode treeNode) {/*** 层次遍历使用到了广度优先搜索，技巧：深度优先用递归，广度优先用队列。*/Queue<TreeNode> queue = new LinkedList<>();List<TreeNode> list = new LinkedList<>();queue.add(treeNode);while (queue.size()>0){//出一个，进n个//出一个TreeNode node = queue.poll();list.add(node);//进n个List<TreeNode> childens = node.childrens;for (TreeNode childNode : childens) {queue.add(childNode);}}return list;}}

注：代码中实现的是一个普通的树，不是一颗二叉树。