层次遍历（LevelOrder）就是默认为自上而下，从左到右，一层一层进行遍历，
层次遍历需要借助队列来完成，
队列：先进先出（FIFO）。

分析：如图有一棵二叉树，按照层次遍历最终的结果就是ABCDEFG，首先将根结点A入队列。

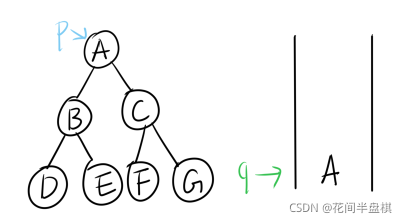
然后根结点出队，并访问A结点，发现A结点既有左孩子也有右孩子，那么就分别将左右孩子入队，此时队列中有BC。

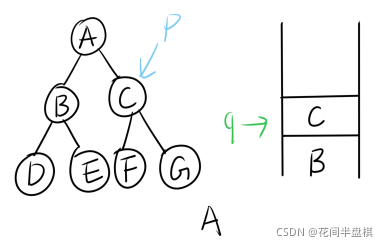
A的左右孩子都入队了，然后将队头结点B出队并访问，此时序列为AB，B有左右孩子，所以将B的左右孩子DE入队，队中此时有CDE。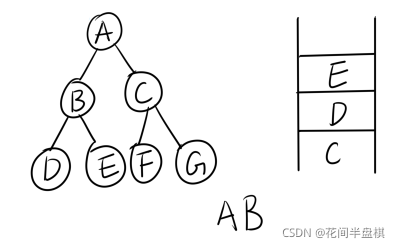
然后队头结点C出队并访问，C有左右孩子，所以将C的左右孩子FG入队。此时队列里有DEFG。

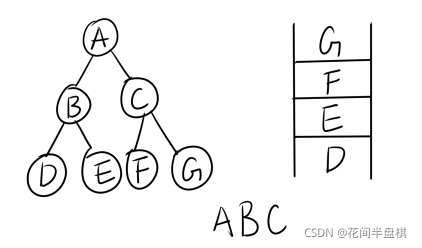
然后队头结点D出队并访问，D没有左右孩子，所以没有可入队的结点。
继续让队头结点E出队并访问，E没有左右孩子，所以没有可入队的结点。
FG同理，此时队列为空，结束。最终层次遍历序列为：ABCDEFG。

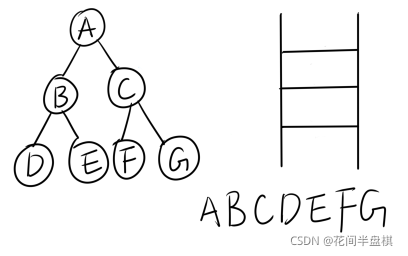
算法思想：层次遍历使用一个队列（先进先出），将根结点入队，出队，然后访问出队结点，若它有左孩子，就将左孩子入队，若它有右孩子，就将右孩子入队，然后访问队头结点，如此循环下去，直到队列为空，就结束了。
代码：

void LevelOrder(BiTree T){  // 全篇❤InitQueue(Q); // 初始化队列Q，队列通常用Q表示，栈用S表示BiTree *p;EnQueue(Q,T); // 将根结点入队while(!IsEmpty(Q)){ // 队列不为空则进入循环DeQueue(Q,p);  // 出队，即将队头结点出队，因为队列先进先出visit(p);  // 并访问，即加入到最终遍历序列中if(p->lchild!=NULL)  // 如果有左孩子EnQueue(Q,p->lchild);  // 就将左孩子入队if(p->rchild!=NULL)  // 如果有右孩子EnQueue(Q,p->rchild);  // 就将右孩子入队}
}

注解：