树的应用 —— 二叉树的遍历【层次遍历、遍历序列还原树】
【层次遍历】
二叉树的遍历一般有先序遍历、中序遍历和后序遍历,除了这三种遍历,还有另一种遍历方式——层次遍历,即按照层次的顺序从左向右进行遍历。
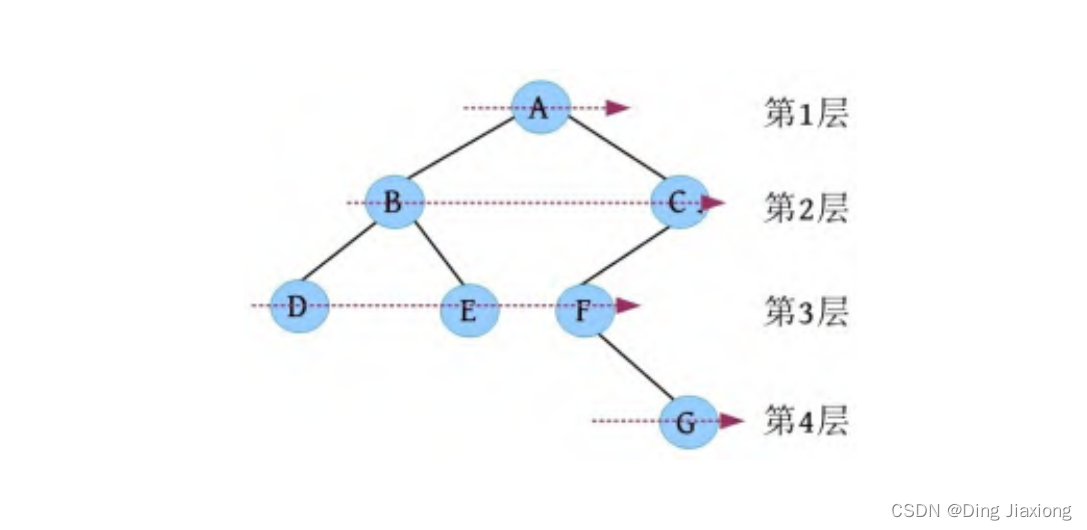
一棵树如下图所示。
层次遍历的流程:首先遍历第1层A,然后遍历第2层,从左向右B、C,再遍历第3层,从左向右D、E、F,再遍历第4层G。
[层次遍历的秘籍]
首先遍历第1层,然后第2层……同一层按照从左向右的顺序访问,直到最后一层。
[程序如何实现层次遍历?]
通过观察可以发现,先被访问的节点,其孩子也先被访问,先来先服务,因此可以用队列实现。
[完美图解]

以上图的二叉树为例,展示层次遍历的过程。
① 首先创建一个队列Q ,令树根入队,如下图所示(注意: 实际上是指向树根A的指针入队,为了图解方便,将数据入队)。
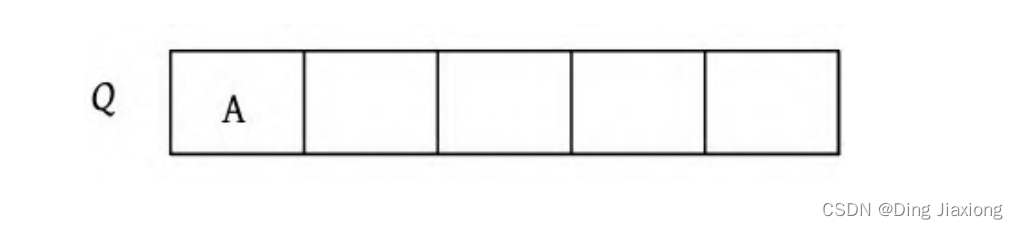
② 队头元素出队,输出A,同时令A的孩子B、C入队(按从左向右的顺序进行,如果是普通树,则包含所有孩子)。二叉树和队列的状态如下图所示。
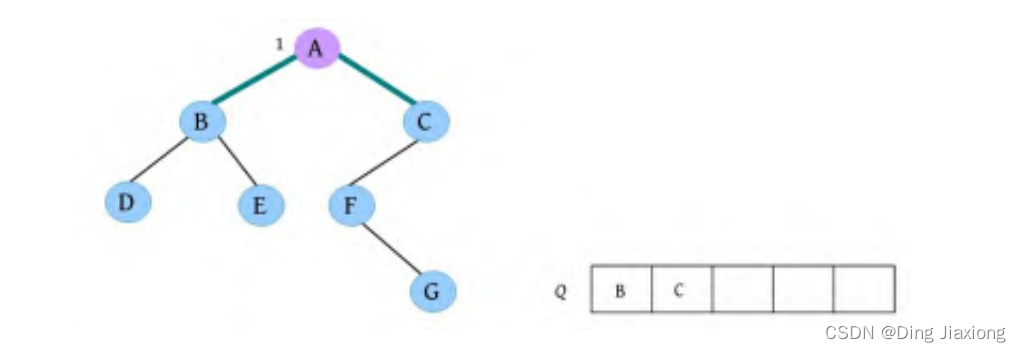
③ 队头元素出队,输出B,同时令B的孩子D、E入队,如下图所示。
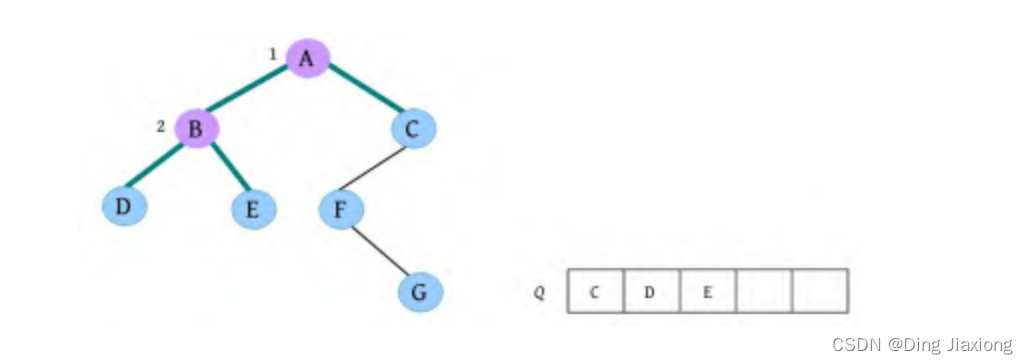
④ 队头元素出队,输出C,同时令C的孩子F入队。二叉树和队列的状态如下图所示。
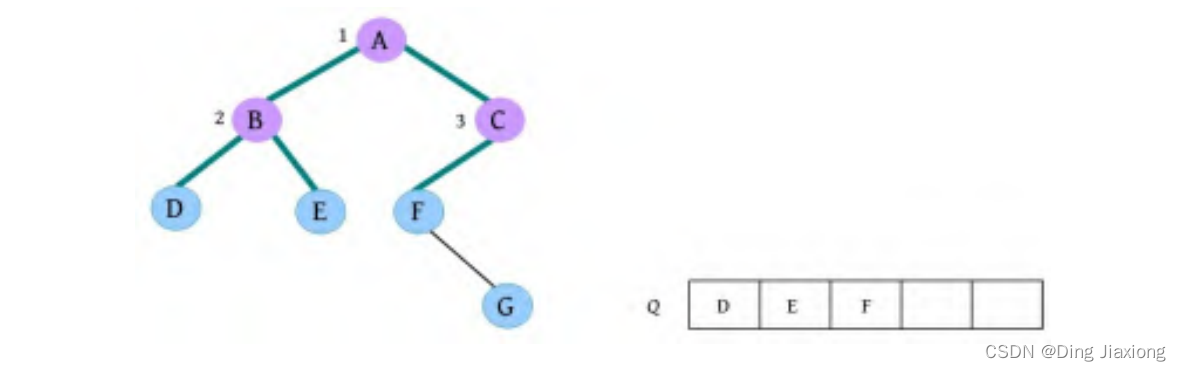
⑤ 队头元素出队,输出D,同时令D的孩子入队,D没有孩子,什么也不做。
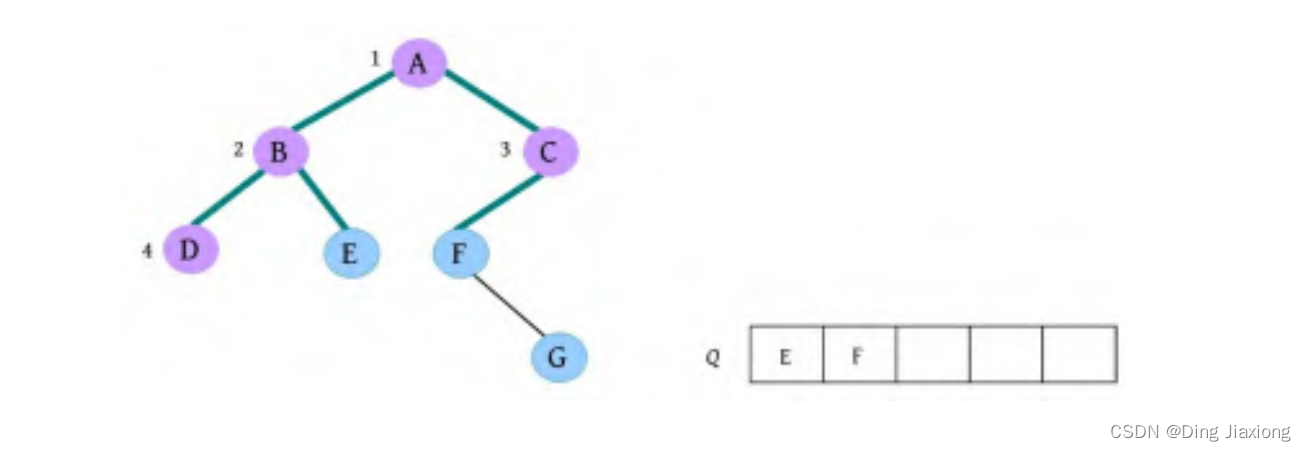
⑥ 队头元素出队,输出E,同时令E的孩子入队,E没有孩子,什么也不做。
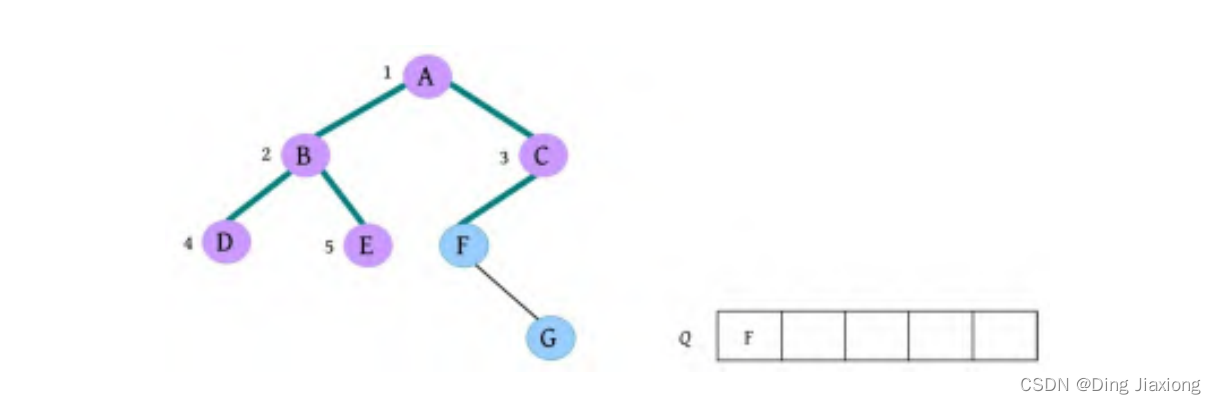
⑦ 队头元素出队,输出F,同时令F的孩子G入队。二叉树和队列的状态如下图所示。
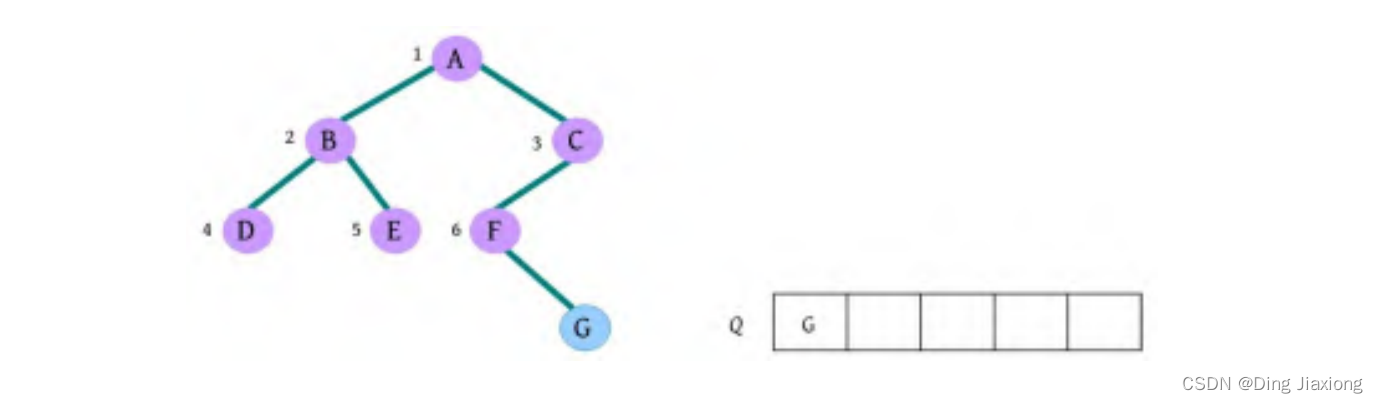
⑧ 队头元素出队,输出G,同时令G的孩子入队,G没有孩子,什么也不做。
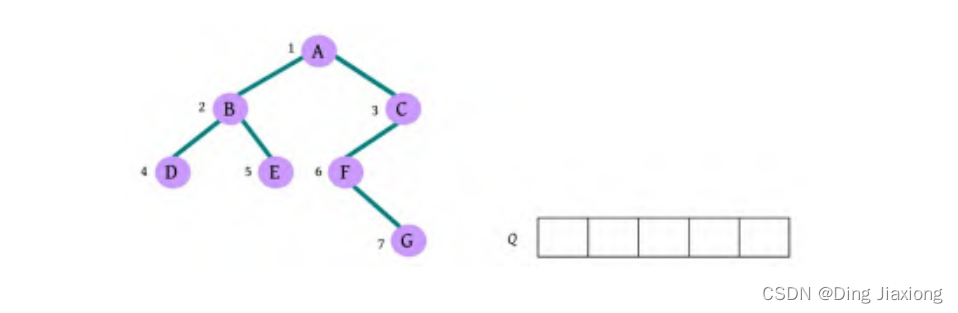
⑨ 队列为空,算法结束。
[算法代码]
void Leveltraverse(Btree T){Btree p;if(!T){return false;}queue<Btree>Q; //创建一个普通队列【先进先出】,里面存放指针类型Q.push(T); //根指针入队while(!Q.empty){ //如果队列不空p = Q.front(); //取出队头元素作为当前节点Q.pop(); //队头元素出队cout << p->data << " ";if(p->lchild){Q.push(p->lchild); //左孩子指针入队}if(p->rchild){Q.push(p->rchild); //右孩子指针入队}}return true;
}
【遍历序列还原树】
根据遍历序列可以还原这棵树,包括二叉树还原、树还原和森林还原三种还原方式。
一 [二叉树还原]
由二叉树的先序和中序序列,或者中序和后序序列,可以唯一地还原一棵二叉树。
注意:【由二叉树的先序和后序序列不能唯一地还原一棵二叉树。】
[算法步骤]
① 先序序列的第1个字符为根
② 在中序序列中,以根为中心划分左、右子树;
③ 还原左、右子树。
[完美图解]
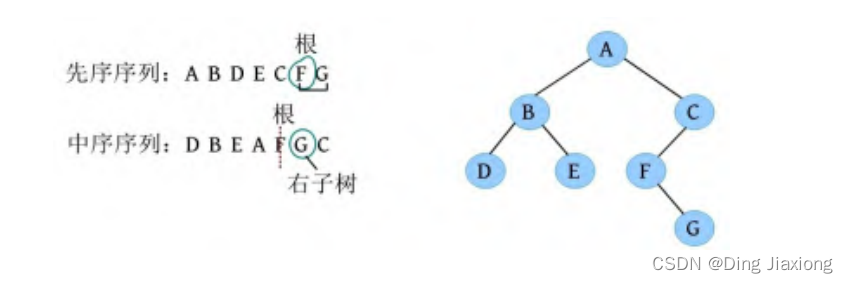
已知一棵二叉树的先序序列ABDECFG和中序序列DBEAFGC,还原这棵二叉树。
① 先序序列的第1个字符A为根,在中序序列中以A为中心划分左、右子树,左子树包含D、B、E三个节点,右子树包含F、G、C三个节点。
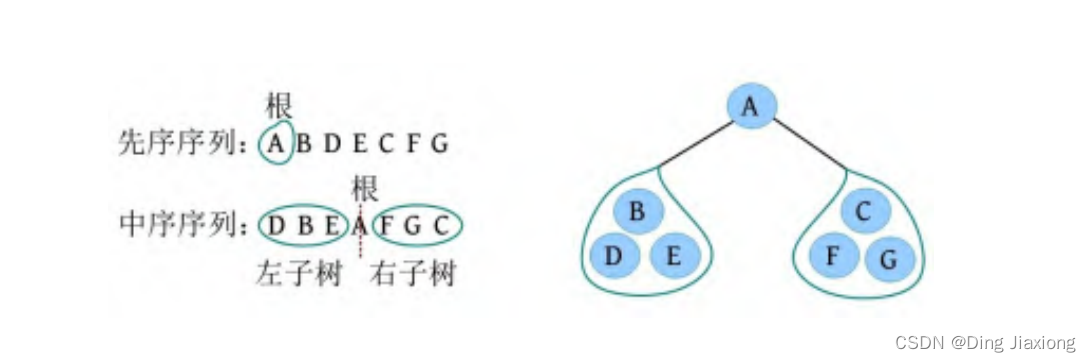
② 左子树DBE,在先序序列中的顺序为BDE,第1个字符B为根,在中序序列中以B为中心划分左、右子树,左、右子树各只有一个节点,直接作为B的左、右孩子。
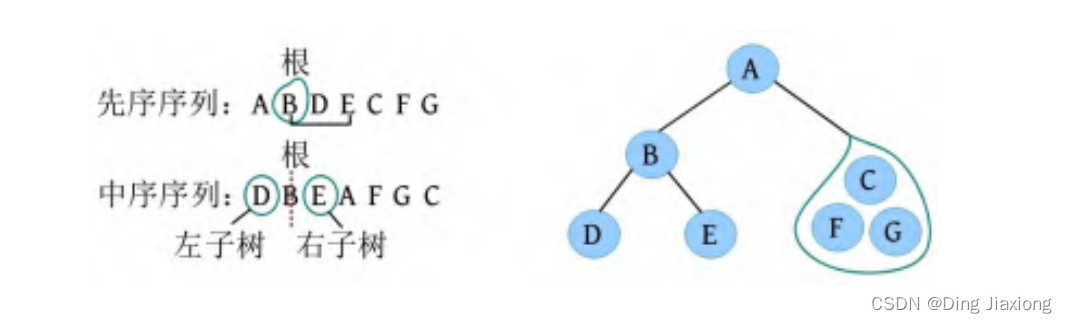
③ 右子树FGC,在先序序列中的顺序为CFG,第1个字符C为根,在中序序列中以C为中心划分左、右子树,左子树包含F、G节点,右子树为空。
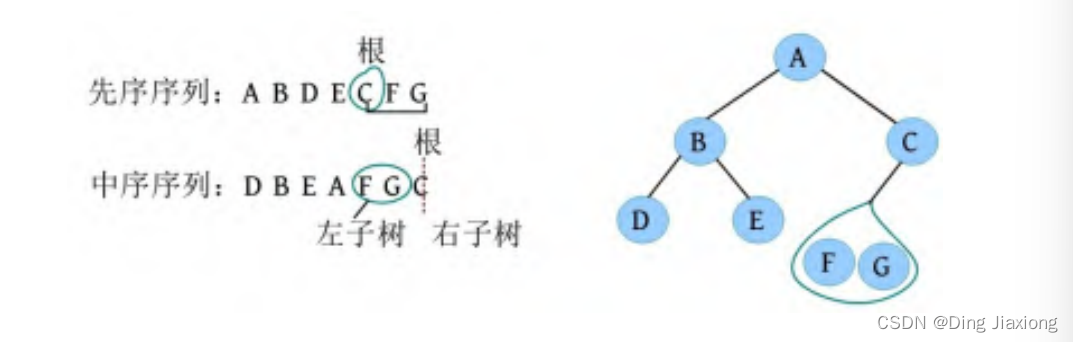
④ 左子树FG,在先序序列中的顺序为FG,第1个字符F为根,在中序序列中以F为中心划分左、右子树,左为空,右子树只有一个节点G,作为F的右孩子即可。
[算法代码]
BiTree pre_mid_createBiTree(char *pre , char *mid, int len){ //由先序、中序还原建立二叉树if(len == 0){return NULL;}char ch = pre[0]; //先序序列中的第1个节点,作为根int index = 0; //在中序序列中查找根节点,并用index 记录查找长度while(mid[index] != ch){ //在中序序列中查找根节点,左边为该节点的左子树,右边为右子树index ++;}BiTree T = new BiTNode; //创建根节点T->data = ch;T->lchild = pre_mid_createBiTree(pre + 1, mid, index); //创建左子树T->rchild = pre_mid_createBiTree(pre + index + 1,mid + index + 1, len - index - 1); //创建右子树return T;
}
[代码解释]
pre_mid_createBiTree(char *pre, char *mid , int len); //由先序、中序还原建立二叉树
函数有三个参数:pre、mid为指针类型,分别指向先序、中序序列的首地址;len为序列的长度。先序和中序的序列长度一定是相同的。
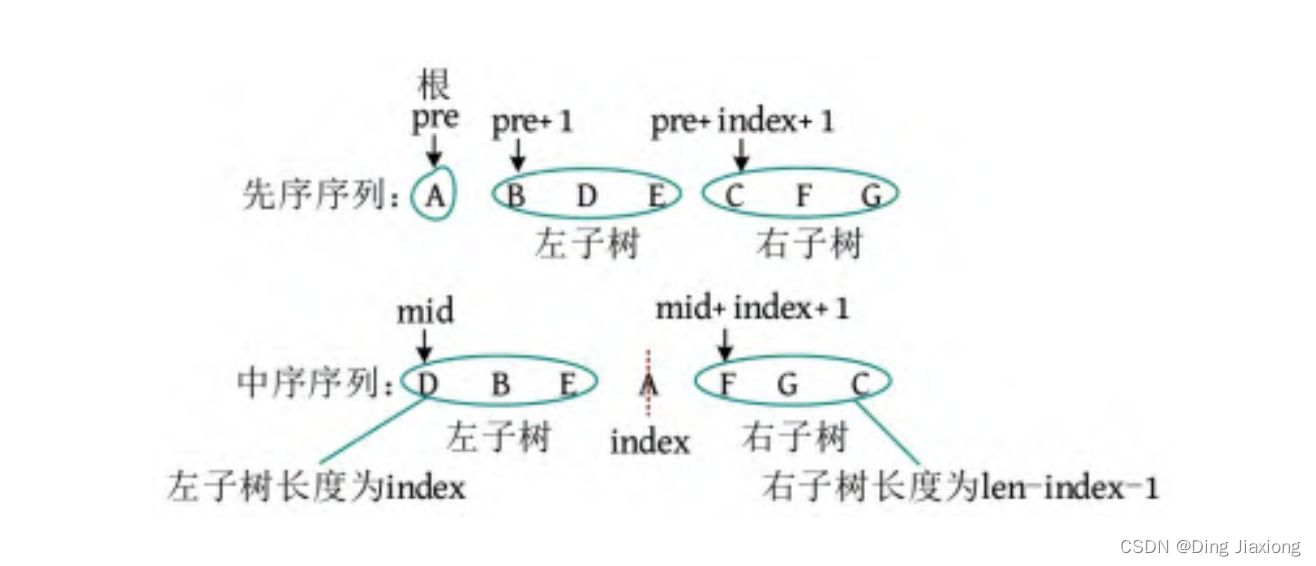
首先,先序序列的第1个字符pre[0]为根;然后,在中序序列中查找根所在的位置,用index记录查找长度,找到后以根为中心,划分为左、右子树。
- 左子树:先序序列的首地址为pre+1,中序序列的首地址为mid,长度为index。
- 右子树:先序序列的首地址为pre+index+1,中序序列的首地址为mid+index+1,长度为len-index-1;右子树的长度为总长度减去左子树的长度,再减去根。
确定参数后,再递归求解左、右子树即可。
第1次的树根及左、右子树划分如下图所示。
由二叉树的后序序列和中序序列也可以唯一确定一棵二叉树,方法和上面一样,只不过后序序列的最后一个字符为根,然后在中序序列中以根为中心划分左、右子树。
[练习]
已知一棵二叉树的后序序列DEBGFCA和中序序列DBEAFGC,还原二叉树。
[算法代码]
BiTree pro_mid_createBiTree(char *last,char *mid , int len){ //由后序、中序还原建立二叉树if(len == 0){return NULL;}char ch = last[len - 1]; //找到后序序列中的最后一个节点,作为根int index = 0; //在中序序列中查找根节点,并用index 记录查找长度while(mid[index] != ch){ //在中序序列中找根节点,左边为该节点的左子树,右边为右子树index ++;}BiTree T = new BiTNode; //创建根节点T->data = ch; T->lchild = pro_mid_createBiTree(last , mid , index); //创建左子树T->rchild = pro_mid_createBiTree(last + index, mid + index + 1,len - index - 1); //创建右子树return T;
}
先序遍历、中序遍历还原二叉树的秘籍:先序找根,中序分左右。
后序遍历、中序遍历还原二叉树的秘籍:后序找根,中序分左右。
二 [树还原]
由于树的先根遍历、后根遍历与其对应二叉树的先序遍历、中序遍历相同,因此可以根据该对应关系,先还原为二叉树,然后把二叉树转换为树。
算法步骤:
- 树的先根遍历、后根遍历与其对应的二叉树的先序遍历、中序遍历相同,因此根据这两个序列,按照先序遍历、中序遍历还原二叉树的方法,还原为二叉树。
- 将该二叉树转换为树
举个栗子:已知一棵树的先根遍历序列ABEFCDGIH和后根遍历序列EFBCIGHDA,还原这棵树。
完美图解:
-
树的先根遍历、后根遍历与其对应的二叉树的先序遍历、中序遍历相同,因此其对应二叉树的先序序列ABEFCDGIH和中序遍历序列EFBCIGHDA,按照先序遍历、中序遍历还原二叉树的方法,还原为二叉树,如下图所示。
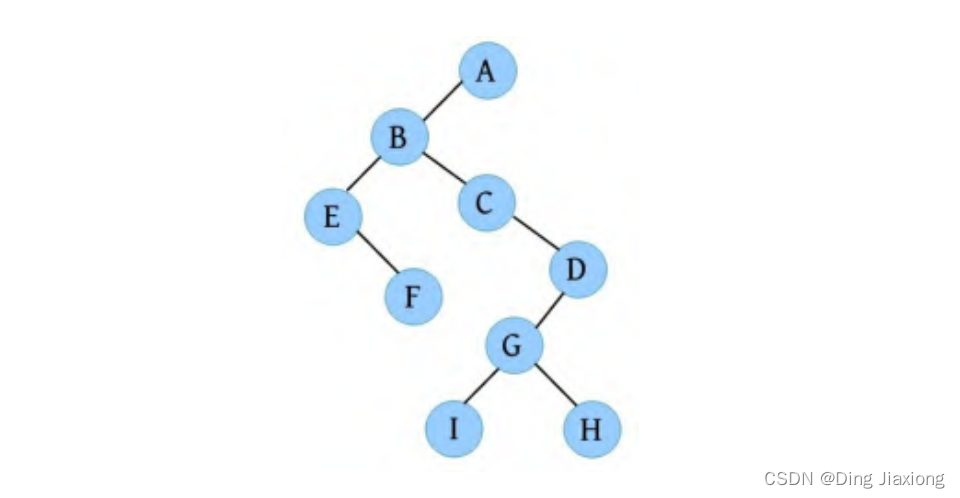
-
按二叉树转换树的规则,将该二叉树转换为树,如下图所示
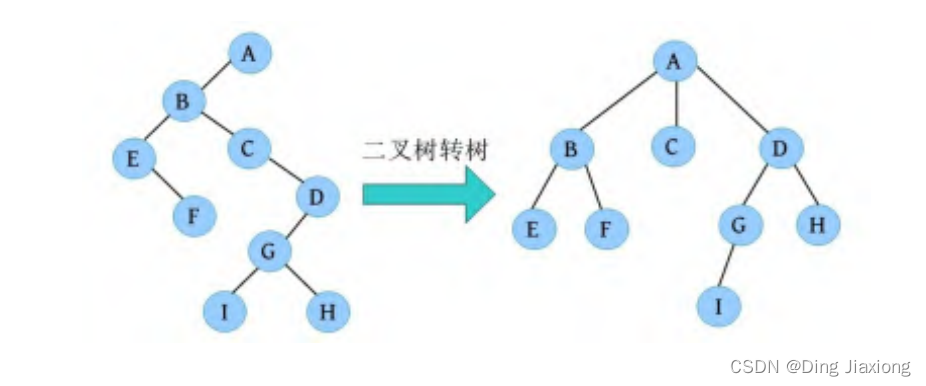
三 [森林还原]
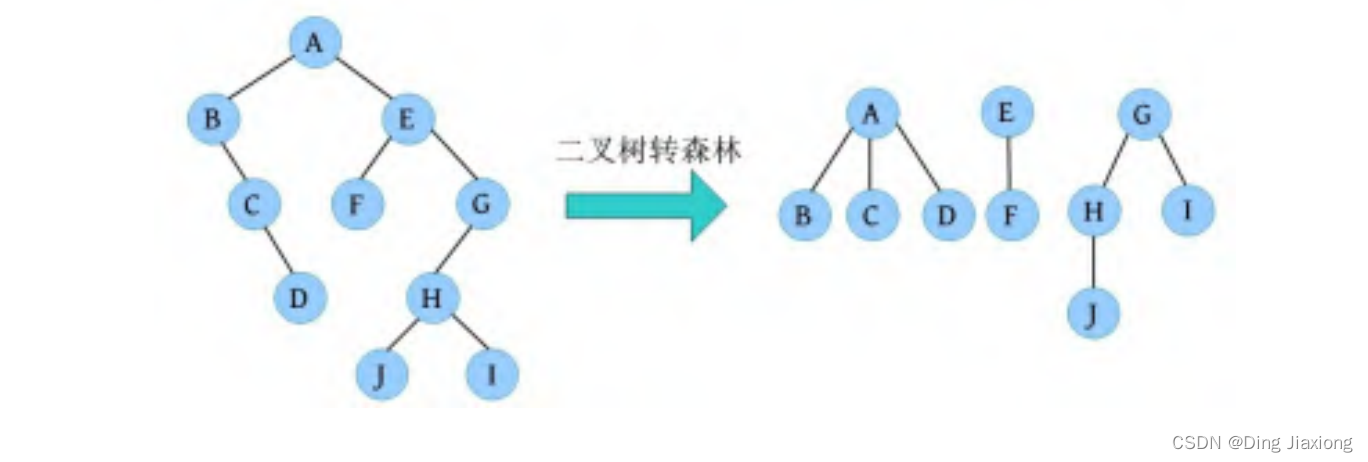
由于森林的先序遍历、中序遍历与其对应二叉树的先序遍历、中序遍历相同,因此可以根据该对应关系,先将其还原为二叉树,然后将二叉树转换为森林。
已知森林的先序遍历序列ABCDEFGHJI和中序遍历序列BCDAFEJHIG,还原森林。
森林的先序和中序对应二叉树的先序和中序,根据该先序和中序序列先将其还原为二叉树,然后将二叉树转换为森林,如下图所示。












![[MATLAB]符号计算](https://img-blog.csdnimg.cn/a4533964eaad43c7ae1faf24f3902ac5.png)
