1. 符号表达式的定义
1.1符号变量的定义
符号变量通过命令syms和sym定义，syms命令一次定义一个或多个符号变量，sym命令一次只能定义一个符号变量。定义好的符号函数可以通过命令symvar检查其自变量。
MATLAB系统有默认的符号自变量，主要为：x、x1、y、y1、z、v、u、t、theta、alpha，默认的规则与平时数学的习惯大致相同。
 当这些变量中的某一个与其他变量组成符号数学表达式时，这个变量即为默认的自变量。
 当这些变量中的某几个组成符号数学表达式时，默认自变量的顺序为：

1.2定义符号表达式

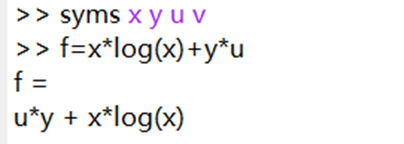
2.符号矩阵的运算


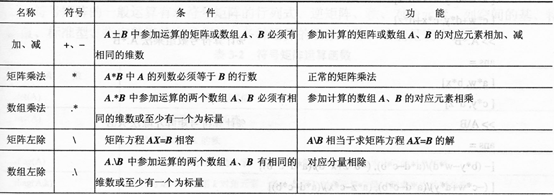
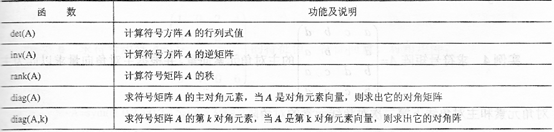
3.符号表达式运算
3.1符号表达式的基本运算
主要包括：合并同类项、表达式展开、因式分解、表达式的化简、提取符号表达式的分子、分母、确定符号矩阵的维数等。


3.2符号表达式中符号变量的操作
findsym(S): 求符号表达式或符号矩阵S中的符号变量。
findsym(S, n): 求符号表达式或符号矩阵S中最靠近x的n个符号变量。
sub(S, old, new): 用变量new替换符号表达式或符号矩阵S中的变量old。
3.3符号函数计算

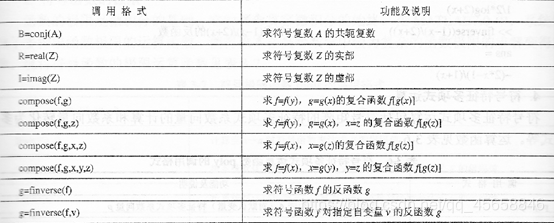
3.4符号微积分
3.4.1符号函数的极限

3.4.2符号函数的导数
diff(S, v, n): 计算符号表达式S对自变量v的n阶导数，v, n可省略。

3.4.3符号函数的积分
int(S, v): 对符号表达式S中的指定变量v求S的不定积分。
int(S, v, a, b): 对符号表达式S中指定变量v在区间[a, b]上求S的定积分。

3.4.4级数求和与函数的级数展开
symsum(S, v, a, b): 对符号表达式S中的指定变量v从a到b求和。（与积分相似）
taylor(S, m, v, a): 对符号函数S在v=a处展开成指定符号变量v的m-1阶泰勒展开式。

3.5符号方程求解
solve(eq, v): 对指定变量v求解方程eq(v)=0的根。
[v1, v2, …, vn]
=solve(eq1, eq2,…, eqn, v1, v2,…vn):
对指定的一组符号变量v1, v2, …, vn求方程组eq1=eq2=…=eqn=0的根。
/: 求符号线性方程组AX=B的解。

3.6 符号积分变换
3.6.1 Laplace变换
L=laplace(F, w, z): 在指定自变量w和指定参变量z的情况下，计算符号函数F的Laplace变换，即:

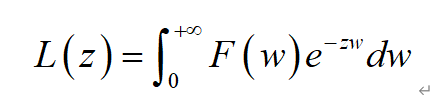
F=ilaplace(L, z, w): 在指定自变量z和指定参变量w的情况下，计算符号函数L的Laplace逆变换，即：

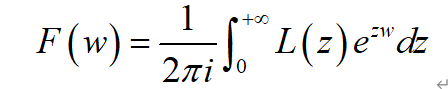
3.6.2 Z变换
L=ztrans(F, w, z): 在指定自变量w和指定参变量z的情况下，计算符号函数F的Z变换。
F=iztrans(L, z, w): 在指定自变量z和指定参变量w的情况下，计算符号函数L的逆Z变换。

3.6.3 傅立叶变换
L=fourier(F, w, z): 在指定自变量w和指定参变量z的情况下，计算符号函数F的Fourier变换。
F=ifourier(L, z, w): 在指定自变量z和指定参变量w的情况下，计算符号函数L的Fourier逆变换。